《理論》〈電気回路〉[H30:問7]重ね合わせの理を用いた抵抗値の算出に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

図のように，直流電圧\( \ E=10 \ \mathrm {V} \ \)の定電圧源，直流電流\( \ I=2 \ \mathrm {A} \ \)の定電流源，スイッチ\(\mathrm {S}\)，\( \ r=1 \ \mathrm {\Omega } \ \)と\(\ R \ \mathrm {[\Omega ]}\)の抵抗からなる直流回路がある。この回路において，スイッチ\(\mathrm {S}\)を閉じたとき，\(\ R \ \mathrm {[\Omega ]} \ \)の抵抗に流れる電流\(I_{\mathrm {R}}\)の値\(\mathrm {[A]}\)が\(\mathrm {S}\)を閉じる前に比べて\(2\)倍に増加した。\(R\)の値\(\mathrm {[\Omega ]}\)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

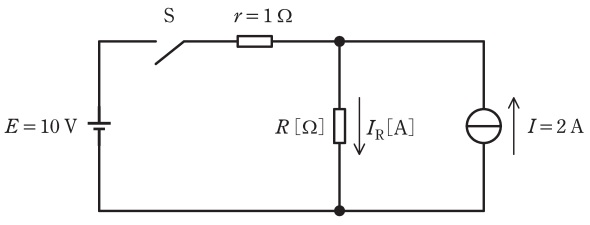
　(1)　\(2\)　　(2)　\(3\)　　(3)　\(8\)　　(4)　\(10\)　　(5)　\(11\)

【ワンポイント解説】

重ね合わせの理を用いる比較的オーソドックスな問題と言えると思います。スイッチ\(\mathrm {S}\)を閉じると，電流源から出る電流が抵抗\(r\)側にも流れることが解くためのポイントとなりそうです。

1.重ね合わせの理
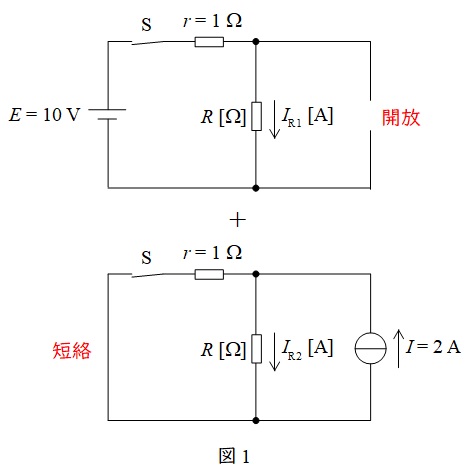
複数の電源で構成された回路は，電源毎に計算した電流を重ね合わせて求めることができます。この時，電圧源は短絡，電流源は開放します。本問においてスイッチ\(\mathrm {S}\)を閉じた回路は図1のように分解できます。

2.分圧・分流の法則
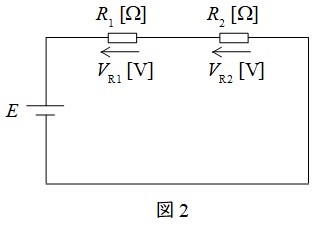
①分圧の法則
図2に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

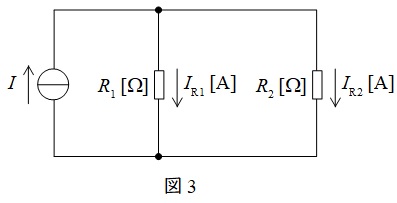
②分流の法則
図3に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　重ね合わせの理の証明

【解答】

解答：(1)
スイッチ\(\mathrm {S}\)が開いている状態では，電流源から流れ出た電流はすべて\(R\)に流れるため，\(I_{\mathrm {R}}=2 \ \mathrm {[A]}\)となる。
題意より，スイッチ\(\mathrm {S}\)が閉じた後，電流が\(2\)倍に増加したので，\(I_{\mathrm {R}}=4 \ \mathrm {[A]}\)となる。

ワンポイント解説「1.重ね合わせの理」の通り，スイッチを閉じた後，重ね合わせの理を適用すると図1のように回路を分解できる。
図1の上側の図において，\(R\)に流れる電流\(I_{\mathrm {R1}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {E}{r+R} \\[ 5pt ] &=&\frac {10}{1+R} \\[ 5pt ] \end{eqnarray}
\] となる。図1の下側の図において，\(R\)に流れる電流\(I_{\mathrm {R2}}\)は，ワンポイント解説「2.分圧・分流の法則」の通り，
\[
\begin{eqnarray}
I_{\mathrm {R2}}&=&\frac {r}{r+R}I \\[ 5pt ] &=&\frac {1}{1+R}\times 2 \\[ 5pt ] &=&\frac {2}{1+R} \\[ 5pt ] \end{eqnarray}
\] となる。よって，\(R\)に流れる電流\(I_{\mathrm {R}}\)は，
\[
\begin{eqnarray}
I_{\mathrm {R}}=I_{\mathrm {R1}}+I_{\mathrm {R2}}&=&4 \\[ 5pt ] \frac {10}{1+R}+\frac {2}{1+R}&=&4 \\[ 5pt ] \end{eqnarray}
\] となるので，\(R\)について解くと，
\[
\begin{eqnarray}
\frac {12}{1+R}&=&4 \\[ 5pt ] 4\left( 1+R\right) &=&12 \\[ 5pt ] 1+R&=&3 \\[ 5pt ] R&=&2 \ [\Omega ] \\[ 5pt ] \end{eqnarray}
\] と求められる。