Contents
指数とは何か
まずはこちらをご覧ください。 \( \ 10 \ \)の右上に小さく\( \ 3 \ \)と書いてあります。
\[
\begin{eqnarray}
10^{3} \\[ 5pt ]
\end{eqnarray}
\]
これは\( \ 10 \ \)を\( \ 3 \ \)回かけた数値です。同じ数を\( \ 3 \ \)回かけることを\( \ 3 \ \)乗というため,“\( \ 10 \ \)の\( \ 3 \ \)じょう”と読みます。
右上に書いた数字(この例では\( \ 3 \ \))を,指数といいます。
実際に計算すると,
\[
\begin{eqnarray}
10^{3}&=&10\times 10\times 10 \\[ 5pt ]
&=&1 \ 000 \\[ 5pt ]
\end{eqnarray}
\]
となります。
同様に\( \ 10 \ \)を\( \ x \ \)乗した数値を,\( \ 10^{x} \ \)と表します。
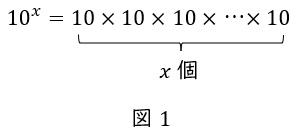
ここまでは簡単ですね。
では,こちらはいかがでしょうか?
\( \ 10 \ \)を \( \ 0 \ \)回かけ算する
\( \ 10 \ \)を\( \ -1 \ \)回かけ算する
\( \ 10 \ \)を\( \ \displaystyle \frac {1}{2} \ \)回かけ算する
急に難しくなりましたが,大丈夫です。詳しく解説していきます。
\( \ 0 \ \)回かけ算するとは?
\( \ 10 \ \)の\( \ 0 \ \)乗は\( \ 1 \ \)です。
\[
\begin{eqnarray}
10^{0}&=&1 \\[ 5pt ]
\end{eqnarray}
\]
しかも\( \ 10 \ \)だけでなく,あらゆる数字において\( \ 0 \ \)乗は\( \ 1 \ \)です。
” \( \ 0 \ \) 乗すると \( \ 1 \ \) ”は,必ず覚えておきましょう。
\( \ 10 \ \)を\( \ 0 \ \)回かけ算する,つまり\( \ 1 \ \)回もかけ算しないのだから,\( \ 10^{0}=0 \ \)なのでは?と思う方もいるでしょう。どうして\( \ 1 \ \)なのでしょうか。
例えば \( \ 10^{x} \ \)を,\( \ x \ \)を\( \ 3 , 2 , 1 \ \)と\( \ 1 \ \)ずつ減らして並べてみましょう。
指数の\( \ x \ \)が\( \ 1 \ \)減ると,\( \ 10^{x} \ \)は\( \ \displaystyle \frac {1}{10} \ \)倍になります。
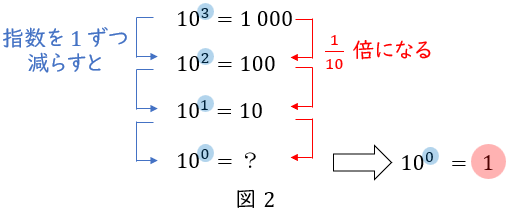
これが\( \ 10^{0} \ \)でも成り立ってほしいので,\( \ 10^{0}=1 \ \)と定義したということです。
したがって,\( \ 10^{0} \ \)がいくつか分からない場合は\( \ 10^{2}=100 \ \),\( \ 10^{1}=10 \ \)と順に書いてみましょう。
“\( \ 0 \ \)乗すると\( \ 1 \ \)”をイメージできるたとえ話
もっと直感的に理解するために,こんなお話はいかがでしょうか。
ある人が風邪をひきました。\( \ 1 \ \)日で\( \ 10 \ \)人にうつして治ったとします。今,風邪をひいているのは\( \ 10 \ \)人です。
\( \ 1 \ \)日目,その\( \ 10 \ \)人が,それぞれ\( \ 10 \ \)人にうつして治ったとします。今,風邪をひいているのは\( \ 100 \ \)人です。
\( \ 2 \ \)日目,その\( \ 100 \ \)人が,それぞれ\( \ 10 \ \)人に風邪をうつして…
…なんとも嫌な話ですね。
このとき,\( \ n \ \)日目に風邪をひいているのは\( \ 10^{n} \ \)人です。
そして初日(\( \ 0 \ \)日目)には,最初に風邪をひいた\( \ 1 \ \)人がいます。したがって,\( \ 10^{0}=1 \ \)となります。
\( \ -1 \ \)回かけ算するとは?
\( \ 10 \ \)の\( \ -1 \ \)乗は\( \ \displaystyle \frac {1}{10} \ \)です。
\[
\begin{eqnarray}
10^{-1}&=&\displaystyle \frac {1}{10} \\[ 5pt ]
\end{eqnarray}
\]
これも,指数が\( \ 1 \ \)減ると\( \ \displaystyle \frac {1}{10} \ \)倍になる,という規則性で理解できます。
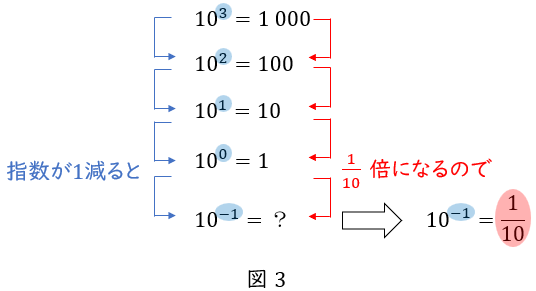
同じ考え方で,\( \ 10 \ \)の\( \ -2 \ \)乗は,\( \ \displaystyle \frac {1}{100} \ \)であり,\( \ 10 \ \)の\( \ -3 \ \)乗は,\( \ \displaystyle \frac {1}{1 \ 000} \ \)です。
つまり 指数のマイナス=逆数 です。
したがって,もし分母にマイナスの指数がある場合は,マイナスを外して分子に移動させましょう。
\[
\begin{eqnarray}
\displaystyle \frac {1}{10^{-2}}&=&10^{2} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \displaystyle \frac {1}{2} \ \)回かけ算するとは?
\( \ 10 \ \)の\( \ \displaystyle \frac {1}{2} \ \)乗は\( \ \sqrt{ 10 } \ \)です。
\[
\begin{eqnarray}
10^{\frac {1}{2}}&=&\sqrt{ 10 } \\[ 5pt ]
\end{eqnarray}
\]
こちらも,証明すべき内容というよりは定義なのですが,
直感的に理解したい方は,\( \ \sqrt{ 10 } \ \)が何かを思い出しましょう。
\( \ 2 \ \)回かけ算して\( \ 10 \ \)になる数です。
\[
\begin{eqnarray}
\sqrt{ 10 } \times \sqrt{ 10 }&=&10=&10^{1} \\[ 5pt ]
\end{eqnarray}
\]
\( \ 2 \ \)回かけ算して\( \ 10 \ \)の\( \ 1 \ \)乗ですから,\( \ \sqrt{ 10 } \ \)をルートではなく指数で表すと,\( \ 1 \ \)を\( \ 2 \ \)で割って,\( \ \displaystyle \frac {1}{2} \ \)乗となります。
\[
\begin{eqnarray}
\sqrt{ 10 }&=&10^{\frac {1}{2}} \\[ 5pt ]
\end{eqnarray}
\]
同じ理屈で,\( \ \sqrt[ 3 ]{ 10 } \ \)は\( \ 3 \ \)回かけ算して\( \ 10 \ \)になる数ですから,
\[
\begin{eqnarray}
\sqrt[ 3 ]{ 10 } \times \sqrt[ 3 ]{ 10 }\times \sqrt[ 3 ]{ 10 }&=&10=&10^{1} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \sqrt[ 3 ]{ 10 } \ \)をルートではなく指数で表すと,\( \ 1 \ \)を\( \ 3 \ \)で割って,\( \ \displaystyle \frac {1}{3} \ \)乗となります。
\[
\begin{eqnarray}
\sqrt[ 3 ]{ 10 }&=&10^{\frac {1}{3}} \\[ 5pt ]
\end{eqnarray}
\]
【補足】指数は小数で書いても構いません。
\[
\begin{eqnarray}
\sqrt{ 10 }&=&10^{\frac {1}{2}}=&10^{0.5} \\[ 5pt ]
\end{eqnarray}
\]
【練習問題】
次の値を求めましょう。
\( (1) \) \( \ 2^{3} \ \)
\( (2) \) \( \ 10^{4} \ \)
\( (3) \) \( \ 5^{-3} \ \)
\( (4) \) \( \ 3^{-4} \ \)
\( (5) \) \( \ \displaystyle \frac {1}{7^{-2}} \ \)
\( (6) \) \( \ \displaystyle \frac {2}{10^{-2}} \ \)
\( (7) \) \( \ 4^{\frac {1}{2}}\ \)
\( (8) \) \( \ \displaystyle \frac {1}{16^{-\frac {1}{2}}} \ \)
\( (9) \) \( \ 14^{0} \ \)
\( (10) \) \( \ 0.5^{-2} \ \)
\( (1) \) \( \ 2^{3} = 2 \times 2 \times 2 = 8 \ \)
\( (2) \) \( \ 10^{4} = 10 \times 10 \times 10 \times 10 = 10 \ 000 \ \)
\( (3) \) \( \ 5^{-3} = \displaystyle \frac {1}{5^{3}} = \displaystyle \frac {1}{5 \times 5 \times 5} = \displaystyle \frac {1}{125} \ \)
\( (4) \) \( \ 3^{-4} = \displaystyle \frac {1}{3^{4}} = \displaystyle \frac {1}{3 \times 3 \times 3 \times 3} = \displaystyle \frac {1}{81} \ \)
\( (5) \) \( \ \displaystyle \frac {1}{7^{-2}} = 7^{2} = 49 \ \)
\( (6) \) \( \ \displaystyle \frac {2}{10^{-2}} = 2 \times \displaystyle \frac {1}{10^{-2}} = 2 \times {10^{2}} = 2 \times 10 \times 10 = 200\ \)
\( (7) \) \( \ 4^{\frac {1}{2}} = \sqrt{4} = 2 \ \)
\( (8) \) \( \ \displaystyle \frac {1}{16^{-\frac {1}{2}}} = 16^{\frac {1}{2}} = \sqrt{16} = 4 \ \)
\( (9) \) \( \ 14^{0}=1 \ \)
\( (10) \) \( \ 0.5^{-2}= \left( \displaystyle \frac{1}{2} \right)^{-2} = 2^{2}=4 \ \)


