指数法則とは
指数法則とは以下の通りです。
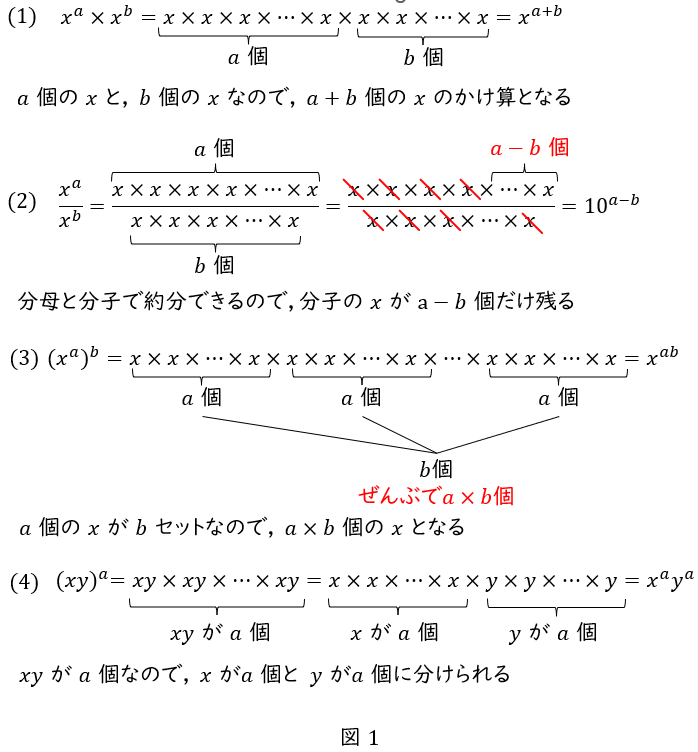
\( (1) \) \( \ x^{a} \times x^{b}=x^{a+b} \ \)
\( (2) \) \( \ \displaystyle \frac {x^a}{x^b} =x^{a-b} \ \)
\( (3) \) \( \ (x^a)^{b}=x^{ab} \ \)
\( (4) \) \( \ (xy)^{a}=x^ay^a \ \)
※指数法則が成り立つのは,\( \ x,y \ \)が正の実数,\( \ a,b \ \)が実数のときですが,
電験については気にする必要がありませんので,説明は割愛させていただきます。
指数法則は難しそうに見えますが,実際に書いてみるとすんなり納得できると思います。
【練習問題】
次の値を求めましょう。ただし,(1)及び(3)は指数の形で求めて下さい。
\( (1) \) \( \ 2^{3} \times 2^{2} \ \)
\( (2) \) \( \ 10^{4} \div 10^{3} \ \)
\( (3) \) \( \ (5^{3})^{2} \ \)
\( (4) \) \( \ (3x)^{4} \ \)
\( (5) \) \( \ \ x^{-5} \div x^{-5} \ \)(ただし\( \ x≠0 \ \)とする。)
\( (6) \) \( \ 5^{3} \times 5^{-2} \div 5^{-2} \ \)
\( (7) \) \( \ 2^{3} \times(2^{3})^{-2} \div 2^{-4} \ \)
\( (8) \) \( \ (x^{0} \times y^{-4})^{\frac {1}{2}}\ \)
\( (1) \) \( \ 2^{3} \times 2^{2} = 2^{3+2} = 2^{5} \ \)
\( (2) \) \( \ 10^{4} \div 10^{3} = 10^{4-3} = 10^{1} = 10 \ \)
\( (3) \) \( \ (5^{3})^{2} = 5^{3 \times 2} = 5^{6} \ \)
\( (4) \) \( \ (3x)^{4} = 3^{4} \times x^{4} = 81x^{4} \ \)
\( (5) \) \( \ \ x^{-5} \div x^{-5} = x^{-5-(-5)} = x^{-5+5} =x^{0} = 1 \ \)
\( (6) \) \( \ 5^{3} \times 5^{-2} \div 5^{-2} = 5^{3+(-2)-(-2)} = 5^{3-2+2} = 5^{3} = 125 \ \)
\( (7) \) \( \ 2^{3} \times(2^{3})^{-2} \div 2^{-4} = 2^{3} \times 2^{-6} \div 2^{-4} = 2^{3+(-6)-(-4)} = 2^{3-6+4} = 2^{1} = 2 \ \)
\( (8) \) \( \ (x^{0}y^{-4})^{\frac {1}{2}} = x^{0 \times \frac {1}{2}}y^{-4 \times \frac {1}{2}} = x^{0}y^{-2} =1 \times y^{-2} = y^{-2} \ \)


