計算をミスを防ぐコツをお伝えします。
Contents
コツ① 普通の数値と,\( \ 10 \ \)の何乗を分ける
例えばこういう式があるとします。
\[
\begin{eqnarray}
\displaystyle \frac {6 \times 10^{-5} \times 0.3^{2}}{2 \times 10^{-8} \times 3 \times 10^{-8}} \\[ 5pt ]
\end{eqnarray}
\]
まずは計算は一切せずに,分けることに集中します。
前半を普通の数値,後半を\( \ 10 \ \)の何乗にします。
このときのポイントは,計算は一切しないことです。
\[
\begin{eqnarray}
\displaystyle \frac {6 \times 0.3^{2}}{2 \times 3 } \times \displaystyle \frac {10^{-5} }{ 10^{-8} \times 10^{-8} } \\[ 5pt ]
\end{eqnarray}
\]
こうして分けておいてから,前半と後半を計算します。
前半は分子の\( \ 6 \ \)と,分母の\( \ 2 \times 3 \ \)が約分できますから,\( \ 0.3^{2}=0.09 \ \)だけが残りますね。
後半は,
\[
\begin{eqnarray}
\displaystyle \frac {10^{-5} }{ 10^{-8} \times 10^{-8} } &=& 10^{-5-(-8)-(-8)} &=& 10^{-5+8+8} &=& 10^{11} \\[ 5pt ]
\end{eqnarray}
\]
となります。
したがって,前半と後半とを合わせて,
\[
\begin{eqnarray}
0.09 \times 10^{11} &=& 9 \times 10^{9} \\[ 5pt ]
\end{eqnarray}
\]
となります。
繰り返しますが,大切なのは,分けている間は計算しないことです。
\[
\begin{eqnarray}
\displaystyle \frac {6 \times 10^{-5} \times 0.3^{2}}{2 \times 10^{-8} \times 3 \times 10^{-8}} \\[ 5pt ]
\end{eqnarray}
\]
例えばこの例だと,分子の\( \ 6 \ \)と,分母の\( \ 2 \times 3 \ \)が約分できることや,\( \ 0.3^{2}=0.09 \ \)がすぐに分かりますが,我慢します。
なぜなら,少なくない受験生が,計算に気を取られて\( \ 10 \ \)の何乗を丸ごと見落とす,などのケアレスミスをするからです。
先の例だと,分子の\( \ 6 \ \)と,分母の\( \ 2 \ \)と\( \ 3 \ \)が約分できることに気が付いて,分母の\( \ 2 \ \)と\( \ 3 \ \)を斜線で消すうちに,その間にある\( \ 10^{-8} \ \)を,丸ごと見落とします。
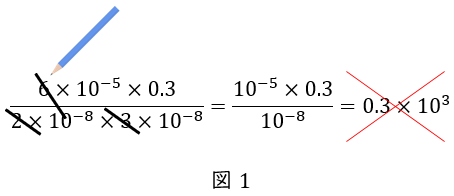
また,本番では手書きで計算していますから,\( \ 10^{-8} \ \)を急いで書くあまり,\( \ 10-8 \ \)に見間違えてしまった,なんてことも。
そんなバカなと思うかもしれませんが,ケアレスミスとはそういうものです。
指数の計算は,まずは普通の数値と,\( \ 10 \ \)の何乗を分けることだけに集中する,というステップを踏めば,ミスをかなり減らせます。
コツ② 大きい数,小さい数は,\( \ 10 \ \)の何乗に書き換える
例えばこのように書き換えます。
\( \ 10 \ 000 = 1 \times 10^{4} \ \)
\( \ 0.000 \ 1 = 1 \times 10^{-4} \ \)
同様に,ぴったり\( \ 10 \ \)の何乗の数でない場合も,
「\( \ 1 \ \)以上\( \ 10 \ \)未満の数 × \( \ 10 \ \)の何乗 」の形に書き換えます。
\( \ 12 \ 345 = 1.234 \ 5 \times 10^{4} \ \)
\( \ 0.000 \ 567 = 5.67 \times 10^{-4} \ \)
こうすると,何が良いのでしょうか?
こういう式があるとします。
\[
\begin{eqnarray}
\displaystyle \frac {8.1 \times 10^{7}}{25 \ 000} \\[ 5pt ]
\end{eqnarray}
\]
まずは,ミスしやすい解き方をご覧ください。
数値と\( \ 10 \ \)の何乗とを分けて,\( \ \displaystyle \frac {8.1}{25 \ 000} \times 10^{7}\ \)として,\( \ 8.1 \div 25 \ 000\ \)を電卓で計算します。
電卓には\( \ 0.000 \ 324 \ \)と出てきます。
これをに,\( \ 10^{7} \ \)をかけるので,小数点を右に\( \ 7 \ \)つ移動させて,答えは\( \ 3 \ 240 \ \)です。
このやり方では,ミスしやすい箇所が多いうえに,ミスに自分で気が付くことができません。
例えば電卓で\( \ 25 \ 000 \ \)を打つとき,\( \ 0 \ \)の数を打ち間違えたとします。
しかし,電卓には小数点以下の数値がずらっと並びますから,\( \ 0 \ \)の数が多い・少ないことに気が付けないのです。
\( \ 0.000 \ 324 \ \)か,\( \ 0.003 \ 24 \ \)か,\( \ 0.000 \ 032 \ 4 \ \)か,パッと見で分かりませんよね。
さらに,最後に,小数点を右に\( \ 7 \ \)つ移動させるときにも,本番中は焦っているので,数え間違えるかもしれません。
一方,こうするとミスを防げます。
始めに\( \ 25 \ 000 \ \)を,\( \ 2.5 \times 10^{4} \ \)にしておくのです。
\[
\begin{eqnarray}
\displaystyle \frac {8.1 \times 10^{7}}{25 \ 000}&=&\displaystyle \frac {8.1 \times 10^{7}}{2.5 \times 10^{4}}\\[ 5pt ]
&=&\displaystyle \frac {8.1}{2.5}\times \displaystyle \frac {10^{7}}{10^{4}}\\[ 5pt ]
&=&\displaystyle \frac {8.1}{2.5}\times 10^{7-4}\\[ 5pt ]
&=&\displaystyle \frac {8.1}{2.5}\times 10^{3}
\end{eqnarray}
\]
ここまでくれば,\( \ 8.1 \div 2.5 \ \)を電卓で計算ですが,桁が少ないのでミスしづらいです。
また,ミスしたとしても,自分で気がづけます。
\( \ 8.1 \div 2.5 \ \)の答えは,明らかに\( \ 1 \ \)桁ですよね。
もし\( \ 1 \ \)未満の数や,\( \ 2 \ \)桁の数になったら,入力ミスです。
電卓で\( \ 8.1 \div 2.5 =3.24\ \)を計算し,最後に,\( \ 10^{3} \ \)をかけて,答えは\( \ 3 \ 240 \ \)です。
※なお,電験三種は選択問題ですが,よく桁数を変えた誤答が用意されています。正解の選択肢は特にそうです。
それだけ,桁数のミスが多いということでしょう。
【練習問題】
\( \ (1) \ \) \( \ \displaystyle \frac {1 \times 10^{-8} }{4 \times 10^{-6} \times 0.5 \times 1 \times 10^{-3}} \ \)
\( \ (2) \ \) \( \ \displaystyle \frac {2 \times 10^{3} }{2 \times 10^{3} + 14 \times 10^{3}} \times 12 \ \)
\( \ (3) \ \) \( \ \displaystyle \frac {0.8 \times 10^{-3} }{2} – 0.32 \times 10^{-3} \ \)
\( \ (4) \ \) \( \ \displaystyle \frac {0.3}{4 \times 10^{-3}+2 \times 10^{-3}} \ \)
\( \ (5) \ \) \( \ \displaystyle \frac {20 \times 62 \ 500}{8 \times 40 \times 10^{3}} \ \)
\( \ (6) \ \) \( \ 32 \ 150 \times 24 \times 365 \times 0.6 \ \)
\( \ (7) \ \) \( \ \displaystyle \frac {3.21 \times 10^{12}}{39 \ 100} \ \)
\( \ (8) \ \) \( \ 3.15 \times 10^{-5} \times (3 \times 10^{8})^{2}\ \)
\( \ (9) \ \) \( \ \displaystyle \frac {3 \ 000 \times 10^{3} \times 6.9}{6 \ 000^{2}} \times 100 \ \)
\( \ (1) 5 \ \)
\[
\begin{eqnarray}
\frac {1 \times 10^{-8} }{4 \times 10^{-6} \times 0.5 \times 1 \times 10^{-3}}&=&\frac {1}{4 \times 0.5 \times 1} \times \frac {10^{-8}}{10^{-6} \times 10^{-3}} \\[ 5pt ]
&=&\frac {1}{4 \times 0.5 \times 1} \times 10^{-8-(-6)-(-3)} \\[ 5pt ]
&=&\frac {1}{2} \times 10^{-8+6+3} \\[ 5pt ]
&=&0.5 \times 10^{1} \\[ 5pt ]
&=&5 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (2) 1.5 \ \)
\[
\begin{eqnarray}
\displaystyle \frac {2 \times 10^{3} }{2 \times 10^{3} + 14 \times 10^{3}} \times 12 &=& \displaystyle \frac {2 \times 12 }{(2+14)} \times \displaystyle \frac {10^{3}}{10^{3}} \\[ 5pt ]
&=& \displaystyle \frac {24}{16} \\[ 5pt ]
&=& \displaystyle \frac {3}{2} \\[ 5pt ]
&=& 1.5 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (3) 8 \times 10^{-5} \ \)
\[
\begin{eqnarray}
\displaystyle \frac {0.8 \times 10^{-3} }{2} – 0.32 \times 10^{-3} &=& \left( \displaystyle \frac {0.8}{2} – 0.32 \right) \times 10^{-3}\\[ 5pt ]
&=&(0.4 – 0.32) \times 10^{-3}\\[ 5pt ]
&=& 0.08 \times 10^{-3}\\[ 5pt ]
&=& 8 \times 10^{-5} \\[ 5pt ]
\end{eqnarray}
\]
\( \ (4) 50 \ \)
\[
\begin{eqnarray}
\displaystyle \frac {0.3}{4 \times 10^{-3}+2 \times 10^{-3}} &=& \displaystyle \frac {0.3}{4+2} \times \displaystyle \frac {1}{10^{-3}}\\[ 5pt ]
&=& \displaystyle \frac {0.3}{6} \times {10^{3}}\\[ 5pt ]
&=& \displaystyle \frac {0.1}{2} \times {10^{3}}\\[ 5pt ]
&=& 0.05 \times {10^{3}} \\[ 5pt ]
&=& 50 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (5) 3.9 \ \)
\[
\begin{eqnarray}
\displaystyle \frac {20 \times 62 \ 500}{8 \times 40 \times 10^{3}} &=& \displaystyle \frac {20 \times 6.25 \times 10^{4}}{8 \times 40 \times 10^{3}}\\[ 5pt ]
&=& \displaystyle \frac {20 \times 6.25}{8 \times 40} \times \displaystyle \frac {10^{4}}{10^3}\\[ 5pt ]
&=& \displaystyle \frac {20 \times 6.25}{8 \times 40} \times 10^{4-3} \\[ 5pt ]
&=& \displaystyle \frac {1 \times 6.25}{8 \times 2} \times 10^{1}\\[ 5pt ]
&=& \displaystyle \frac {6.25}{16} \times 10^{1}\\[ 5pt ]
&=& \displaystyle \frac {62.5}{16}\\[ 5pt ]
\end{eqnarray}
\]
ここまで来たら電卓で\( \ 62.5 \div 16\ \)をするのですが,電卓を打ちながら何桁になるかを考えましょう。\( \ 1\ \)桁ですね。電卓を打つと\( \ 3.9\ \)となり,\( \ 1\ \)桁ですから,桁の入力ミスはなさそうだと確認できます。
答えは\( \ 3.9\ \)です。
\( \ (6) 1.69\times 10^{8} \ \)
\[
\begin{eqnarray}
32 \ 150 \times 24 \times 365 \times 0.6 &=&3.215 \times 10^{4} \times 24 \times 3.65 \times 10^{2} \times 0.6 \\[ 5pt ]
&=&3.215 \times 24 \times 3.65 \times 0.6 \times 10^{4+2} \\[ 5pt ]
&=&3.215 \times 24 \times 3.65 \times 0.6 \times 10^{6} \\[ 5pt ]
\end{eqnarray}
\]
ここまで来たら電卓で\( \ 3.215 \times 24 \times 3.65 \times 0.6 \ \)をするのですが,何桁になるか考えましょう。
ざっくり\( \ 3 \times 20 \times 4 \ \)をして,それを\( \ 0.5 \ \)倍,つまり半分にすればいいのです。
\( \ 3 \times 20 \times 4 =240 \ \)の半分で\( \ 120 \ \)ですから,\( \ 3 \ \)桁です。
電卓を打つと,\( \ 169 \ \)となり,\( \ 3\ \)桁ですから,桁の入力ミスはなさそうだと確認できます。
元の式に戻して,答えは\( \ 169 \times 10^{6} = 1.69\times 10^{8} \ \)です。
\( \ (7) 8.2 \times 10^{7} \ \)
\[
\begin{eqnarray}
\displaystyle \frac {3.21 \times 10^{12}}{39 \ 100} &=& \displaystyle \frac {3.21 \times 10^{12}}{3.91 \times 10^{4} } \\[ 5pt ]
&=& \displaystyle \frac {3.21}{3.91} \times \displaystyle \frac {10^{12}}{10^{4} } \\[ 5pt ]
&=& \displaystyle \frac {3.21}{3.91} \times 10^{12-4} \\[ 5pt ]
&=& \displaystyle \frac {3.21}{3.91} \times 10^{8} \\[ 5pt ]
\end{eqnarray}
\]
ここまで来たら電卓で\( \ 3.21 \div 3.91\ \)をするのですが,どれくらいの数になるかを考えましょう。
\( \ 1\ \)にちょっと満たないくらい。\( \ 0.9\ \)くらいですね。
電卓を打つと\( \ 0.82\ \)となるので,入力ミスはなさそうだと確認できます。
元の式に戻して,答えは\( \ 0.82 \times 10^{8}= 8.2 \times 10^{7}\ \)です。
\( \ (8) 2.835 \times 10^{12} \ \)
\[
\begin{eqnarray}
3.15 \times 10^{-5} \times (3 \times 10^{8})^{2} &=& 3.15 \times 10^{-5} \times 3^{2} \times (10^{8})^{2} \\[ 5pt ]
&=& 3.15 \times 3^{2} \times 10^{-5} \times (10^{8})^{2} \\[ 5pt ]
&=& 3.15 \times 9 \times 10^{-5} \times 10^{16} \\[ 5pt ]
&=& 3.15 \times 9 \times 10^{-5+16} \\[ 5pt ]
&=& 3.15 \times 9 \times 10^{11} \\[ 5pt ]
\end{eqnarray}
\]
ここまで来たら電卓で\( \ 3.15 \times 9\ \)をするのですが,何桁になるか考えましょう。\( \ 2\ \)桁ですね。
電卓を打つと,\( \ 28.35 \ \)となり,\( \ 2\ \)桁ですから,桁の入力ミスはなさそうだと確認できます。
元の式に戻して,答えは\( \ 28.35 \times 10^{11} = 2.835 \times 10^{12} \ \)です。
\( \ (9) 57.5 \ \)
\[
\begin{eqnarray}
\displaystyle \frac {3 \ 000 \times 10^{3} \times 6.9}{6 \ 000^{2}} \times 100 &=& \displaystyle \frac {3 \times 10^{3} \times 10^{3} \times 6.9}{6^{2} \times (10^{3})^{2}} \times 10^{2} \\[ 5pt ]
&=& \displaystyle \frac {3 \times 6.9}{6^{2}} \times \displaystyle \frac {10^{3} \times 10^{3} \times 10^{2}}{(10^{3})^{2}} \\[ 5pt ]
&=& \displaystyle \frac {3 \times 6.9}{36} \times \displaystyle \frac {10^{3} \times 10^{3} \times 10^{2}}{10^{6}} \\[ 5pt ]
&=& \displaystyle \frac {3 \times 6.9}{36} \times 10^{3+3+2-6} \\[ 5pt ]
&=& \displaystyle \frac {1 \times 6.9}{12} \times 10^{2} \\[ 5pt ]
\end{eqnarray}
\]
ここまで来たら電卓で\( \ 6.9 \div 12 \ \)をするのですが,どれくらいの数になるかを考えましょう。
\( \ 0.5\ \)より大きく,\( \ 1\ \)より小さい数ですね。
電卓を打つと\( \ 0.575\ \)となるので,入力ミスはなさそうだと確認できます。
元の式に戻して,答えは\( \ 0.575 \times 10^{2}= 57.5 \ \)です。


