Contents
単位とは
重さ\( \ 1 \ \)と言われても,\( \ 1 \ \)グラムなのか,\( \ 1 \ \)ポンドなのか,\( \ 1 \ \)両なのかで大違いですよね。
単位とは,あるものの量を測るために,基準として定められた量のことです。
重さの単位は,グラム,ポンド,両,シリングなど,
長さの単位は,メートル,インチ,尺,マイルなどがあります。
国によって違うと不便なので,世界共通でこの単位を使おう,というのが決まっています。
例えば重さではキログラム,長さではメートルです。
電験における単位の表記
重さ(質量)や長さ,時間,電圧,抵抗などのことを,物理量といいます。
物理量も単位もアルファベットで書かれるのですが,被ることが多々あります。
例えば,電圧は物理量でも\( \ V \ \)ですし,単位でも\( \ \mathrm {V} \ \)です。
慣れてしまえば,なんてことはないのですが,初めは戸惑うかもしれません。
そこで,物理量と単位の書き分け方について解説します。
①物理量は斜め(イタリック体),単位はまっすぐ(ローマン体)
②単位を大カッコ\( \ [ \ ] \ \)で囲むことがある。
この\( \ 2 \ \)つのルールにより,電圧はこのように書くわけです。
\( \ V \ \mathrm {[V]} \ \)
※初めの\( \ V \ \)は物理量なので斜めになっています。
次の\( \ \mathrm {V} \ \)は単位なのでまっすぐで,\( \ [ \ ] \ \)で囲まれています。
ただし,単位は必ず\( \ [ \ ] \ \)で囲まれるというわけではなく,単位の前に数値がくる場合はそのまま書かれます。(ただし,古い年度等は異なる場合があります。)
数値+単位 → そのまま書く
物理量+単位 → 単位を大カッコ\( \ [ \ ] \ \)で囲む
日本語+単位 → 単位を大カッコ\( \ [ \ ] \ \)で囲む
実際の過去問で確認してみましょう。
・導体\( \ \mathrm {A} \ \)には\( \ 1.2 \ \mathrm {A} \ \)の,導体\( \ \mathrm {B} \ \)には\( \ \mathrm {3 \ A} \ \)の電流が流れている。
\( \ \mathrm {A} \ \)と\( \ \mathrm {B} \ \)の間隔が\( \ \ l \ \)\( \ \mathrm {[m]} \ \)のとき…\( \ \ l \ \)の値\( \ \mathrm {[m]} \ \)として最も近いものを…
単位は,数値の後の場合はそのまま,物理量や日本語の後の場合は\( \ [ \ ] \ \)がついています。
電験には多くのアルファベットが出てきますから,勉強し始めの方にとっては,それだけで難しく見えますね。
一つ一つのアルファベットが何を表しているか,焦らず読み解いていきましょう。
接頭語(せっとうご)とは
\( \ \mathrm {kg} \ \)の\( \ \mathrm {k} \ \),\( \ \mathrm {cm} \ \)の\( \ \mathrm {c} \ \)など,単位の前に付くアルファベットのことです。
これは接頭語あるいは接頭辞といい,桁数を表します。
\( \ 10 \ \)の何乗 それぞれにアルファベットが決まっています。
例えば, \( \ 10^{3} \ \)なら\( \ \mathrm {k} \ \)(キロ),\( \ 10^{-3} \ \)なら\( \ \mathrm {m} \ \)(ミリ)です。
では,実際に接頭語を使ってみましょう。
\( \ 1 \ 000 \ \mathrm {g} \ \)を,接頭語を使って表すと,
\( \ 1 \ 000 = 1 \times 10^{3} \ \)であり,\( \ 10^{3} \ \)を表す接頭語は\( \ \mathrm {k} \ \)(キロ)ですから,\( \ 10^{3} \ \)を\( \ \mathrm {k} \ \)に書き換えることができます。
したがって,\( \ 1 \ 000 \ \mathrm {g} = 1 \times 10^{3} \ \mathrm {g} = 1 \ \mathrm {kg} \ \)です。
同じ様に,\( \ 0.001 \ \mathrm {m} \ \)は,
\( \ 0.001 = 1 \times 10^{-3} \ \)であり,\( \ 10^{-3} \ \)を表す接頭語は\( \ \mathrm {m} \ \)(ミリ)ですから,\( \ 10^{-3} \ \)を\( \ \mathrm {m} \ \)に書き換えることができます。
したがって\( \ 0.001 \ \mathrm {m} = 1 \times 10^{-3} \ \mathrm {m} = 1 \ \mathrm {mm} \ \)です。
※同じ\( \ \mathrm {m} \ \)なので分かりにくいのですが,最初の\( \ \mathrm {m} \ \)は接頭語,次の\( \ \mathrm {m} \ \)は長さの単位であるメートル,というわけです。
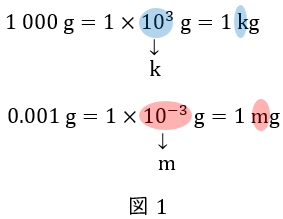
電験で使用する接頭語と,その接頭語をよく使う物理量を,表にまとめました。
| 記号 | 読み方 | 数値 | 意味 | 指数表記 | 電験における使用例 |
|---|---|---|---|---|---|
| \( \ \mathrm {G} \ \) | ギガ | \( \ 1 \ 000 \ 000 \ 000 \ \) | 十億 | \( \ 10^{9} \ \) | \( \ \mathrm {GW} \ \) |
| \( \ \mathrm {M} \ \) | メガ | \( \ 1 \ 000 \ 000 \ \) | 百万 | \( \ 10^{6} \ \) | \( \ \mathrm {M\Omega} \ \),\( \ \mathrm {MHz} \ \) |
| \( \ \mathrm {k} \ \) | キロ | \( \ 1 \ 000 \ \) | 千 | \( \ 10^{3} \ \) | \( \ \mathrm {k\Omega } \ \),\( \ \mathrm {kW } \ \) |
| \( \ \mathrm {h} \ \) | ヘクト | \( \ 100 \ \) | 百 | \( \ 10^{2} \ \) | \( \ \mathrm {hPa} \ \) |
| \( \ \mathrm {d} \ \) | デシ | \( \ 0.1 \ \) | 十分の一 | \( \ 10^{-1} \ \) | \( \ \mathrm {dB} \ \) |
| \( \ \mathrm {c} \ \) | センチ | \( \ 0.01 \ \) | 百分の一 | \( \ 10^{-2} \ \) | \( \ \mathrm {cm} \ \) |
| \( \ \mathrm {m} \ \) | ミリ | \( \ 0.001 \ \) | 千分の一 | \( \ 10^{-3} \ \) | \( \ \mathrm {mm} \ \),\( \ \mathrm {mA} \ \) |
| \( \ \mathrm {\mu} \ \) | マイクロ | \( \ 0.000 \ 001 \ \) | 百万分の一 | \( \ 10^{-6} \ \) | \( \ \mathrm {\mu m} \ \) |
| \( \ \mathrm {n} \ \) | ナノ | \( \ 0.000 \ 000\ 001 \ \) | 十億分の一 | \( \ 10^{-9} \ \) | \( \ \mathrm {nm} \ \),\( \ \mathrm {ns} \ \) |
語呂合わせも考えてみたので,参考までにご覧ください。
・\( \ \mathrm {k} \ \)が\( \ 10^{3} \ \),\( \ \mathrm {M} \ \)が\( \ 10^{6} \ \),\( \ \mathrm {G} \ \)が\( \ 10^{9} \ \)の覚え方
計算問題,ろくにできずにぎっくり腰
けい(\( \ \mathrm {k} \ \))さん(\( \ 3 \ \))も(\( \ \mathrm {M} \ \))んだい,ろく(\( \ 6 \ \))にできず,ぎっ(\( \ \mathrm {G} \ \))く(\( \ 9 \ \))りごし
・\( \ \mathrm {m} \ \)が\( \ 10^{-3} \ \),\( \ \mathrm {\mu } \ \)が\( \ 10^{-6} \ \),\( \ \mathrm {n} \ \)が\( \ 10^{-9} \ \)の覚え方
みみをすませて,マイクで録音,なんて苦しい語呂合わせ
み(\( \ \mathrm {m} \ \))み(\( \ 3 \ \))をすませて,マイク(\( \ \mathrm {\mu } \ \))でろく(\( \ 6 \ \))おん,な(\( \ \mathrm {n} \ \))んてく(\( \ 9 \ \))るしい語呂合わせ
“苦しい語呂合わせ”は,まさにその通りですが,もしお困りでしたら,ご利用ください。
例外:\( \ 1 \ 000 \ \mathrm {kg} \ \)は\( \ 1 \ \mathrm {t} \ \)(トン)
例外として\( \ 1 \ 000 \ \mathrm {kg} \ \)は,\( \ 1 \ \mathrm {Mg} \ \)(メガグラム)とは言わず,\( \ 1 \ \mathrm {t} \ \)(トン)です。
理由を調べてみたのですが,どうやら単純に,使われてきた歴史が長いからのようです。
【練習問題】
\( (1) \) \( \ 2 \ 500 \ \mathrm {Hz} \ \)は,何\( \ \mathrm {[kHz]} \ \)か
\( (2) \) \( \ 8.1 \times 10^{10} \ \mathrm {J} \ \)は,何\( \ \mathrm {[kJ]} \ \)か
\( (3) \) \( \ 169 \ 000 \ 000 \ \mathrm {kW・h} \ \)は,何\( \ \mathrm {[GW・h]} \ \)か
\( (4) \) \( \ 9.24 \times 10^{6} \ \mathrm {kg} \ \)は,何\( \ \mathrm {[t]} \ \)か
\( (5) \) \( \ 0.4 \times 10^{-9} \ \mathrm {s} \ \)を,接頭語を使って,\( \ 10 \ \)の累乗を使わない形で書いてください。
\( (6) \) \( \ 200 \times 10^{6} \ \mathrm {Hz} \ \)を,接頭語を使って,\( \ 10 \ \)の累乗を使わない形で書いてください。
\( (7) \) \( \ 19 \ 200 \ \mathrm {W} \ \)は,何\( \ \mathrm {[kW]} \ \)か
\( (8) \) \( \ 0.004 \ 33 \ \mathrm {V} \ \)は,何\( \ \mathrm {[mV]} \ \)か
\( (1) \) \( \ 2 \ 500 \ \mathrm {Hz} = 2.5 \ \mathrm {kHz} \ \)
\( \ \mathrm {k} \ \)(キロ)は, \( \ 10^{3} \ \)です。単位が\( \ 10^{3} \ \)倍になったので,\( \ = \ \)にするためには,\( \ 2 \ 500 \ \)に\( \ 10^{-3} \ \)をかけます(つまり,小数点を左に\( \ 3 \ \)つ動かします)。したがって,答えは\( \ 2.5 \ \mathrm {kHz} \ \)です。
電験の場合\( \ 3\ \)桁ごとにスペースが入るので,それを目印にしましょう。
\( (2) \) \( \ 8.1 \times 10^{10} \ \mathrm {J} = 8.1 \times 10^{7} \ \mathrm {kJ} \ \)
\( \ \mathrm {k} \ \)(キロ)は\( \ 10^{3} \ \)です。単位が\( \ 10^{3} \ \)倍になったので,\( \ = \ \)にするためには,\( \ 8.1 \times 10^{10} \ \)に\( \ 10^{-3} \ \)をかけます。\( \ 10-3=7 \ \)で,\( \ 8.1 \times 10^{7} \ \mathrm {kJ} \ \)となります。
\( (3) \) \( \ 169 \ 000 \ 000 \ \mathrm {kW・h} = 169 \ \mathrm {GW・h} \ \)
\( \ \mathrm {k} \ \)(キロ)が\( \ 10^{3} \ \),\( \ \mathrm {G} \ \)(ギガ)が\( \ 10^{9} \ \)です。
\( \ 9-3=6 \ \)で,単位が\( \ 10^{6} \ \)倍になったということです。
\( \ = \ \)にするためには,\( \ 10^{-6} \ \)をかけます。\( \ 169 \ 000 \ 000 \ \)の\( \ 0 \ \)を\( \ 6 \ \)個消して,答えは\( \ 169 \ \mathrm {GW・h} \ \)です。
\( (4) \) \( \ 9.24 \times 10^{6} \ \mathrm {kg} = 9.24 \times 10^{3} \ \mathrm {t} \ \)
\( \ 1 \ \mathrm {t} \ \)(トン)は\( \ 1 \ 000 \ \mathrm {kg} \ \)でしたね。
つまり単位が\( \ 10^{3} \ \)倍になったので,\( \ = \ \)にするためには\( \ 10^{-3} \ \)をかけます。\( \ 6-3=3 \ \)で,\( \ 9.24 \times 10^{3} \ \mathrm {t} \ \)です。
\( (5) \) \( \ 0.4 \times 10^{-9} \ \mathrm {s} \ \)を,接頭語を使って,\( \ 10 \ \)の累乗を使わない形で書いてください。
\( \ 10^{-9} \ \)を表す接頭語は,\( \ \mathrm {n} \ \)(ナノ)です。したがって,答えは\( \ 0.4 \ \mathrm {ns} \ \)です。
\( (6) \) \( \ 200 \times 10^{6} \ \mathrm {Hz} = 200 \ \mathrm {MHz} \ \)
\( \ 10^{6} \ \)を表す接頭語は,\( \ \mathrm {M} \ \)(メガ)です。したがって,答えは\( \ 200 \ \mathrm {MHz} \ \)です。
\( (7) \) \( \ 19 \ 200 \ \mathrm {W} = 19.2 \ \mathrm {kW} \ \)
\( \ \mathrm {k} \ \)(キロ)は\( \ 10^{3} \ \)です。単位が\( \ 10^{3} \ \)倍になったので,\( \ = \ \)にするためには,\( \ 10^{-3} \ \)をかけます。したがって,小数点を左に\( \ 3 \ \)つ動かし,答えは\( \ 19.2 \ \mathrm {kW} \ \)です。
\( (8) \) \( \ 0.004 \ 33 \ \mathrm {V} = 4.33 \ \mathrm {mV} \ \)
\( \ \mathrm {m} \ \)(ミリ)は\( \ 10^{-3} \ \)です。単位が\( \ 10^{-3} \ \)倍になったので,\( \ = \ \)にするためには,\( \ 10^{3} \ \)をかけます。したがって,小数点を右に\( \ 3 \ \)つ動かし,答えは\( \ 4.33 \ \mathrm {mV} \ \)です。


