Contents
対数とは何か
対数の前に,まずは指数を説明します。
\[
\begin{eqnarray}
10^{3} \\[ 5pt ]
\end{eqnarray}
\]
これは\( \ 10 \ \)を\( \ 3 \ \)回かけた数値です。同じ数を\( \ 3 \ \)回かけることを\( \ 3 \ \)乗というため,“\( \ 10 \ \)の\( \ 3 \ \)じょう”と読みます。
右上に書いた数字(この例では\( \ 3 \ \))を,指数といいます。
実際に計算すると,
\[
\begin{eqnarray}
10^{3}&=&10\times 10\times 10 \\[ 5pt ]
&=&1 \ 000 \\[ 5pt ]
\end{eqnarray}
\]
となります。
同様に,\( \ 10 \ \)を\( \ x \ \)乗した数値を,\( \ 10^{x} \ \)と表します。
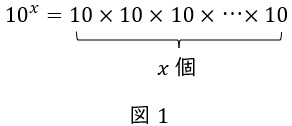
なお,指数の解説ページも作成予定です。完成しましたらこちらにリンクを追加します。
そして対数\( \ \left( \log \right) \ \)とは、指数(右上に書かれた小さな数字)を主役にして表現する方法です。
例えば\( \ 10^{3}=1 \ 000 \ \)であれば,指数の\( \ 3 \ \)を\( \ \log_{10}1 \ 000 \ \)と表現できます。

つまり,\( \ \log_{10}1 \ 000\ \)とは,“\( \ 10 \ \)を\( \ 1 \ 000 \ \)にするには何乗すればよいか”なのです。
【補足】 \( \ \log_{10}1 \ 000\ \)は,“\( \ 1 \ 000 \ \)は\( \ 10 \ \)の何乗か”と考えることもできます。しかし,それでは数値を右から左に読むことになり,横書きの文章を読む順序と逆になってしまいます。したがってこの解説では,\( \ \log_{10}1 \ 000\ \)を“\( \ 10 \ \)を\( \ 1 \ 000 \ \)にするには何乗すればよいか”と考えることで,左から右に読めるようにしています。
一般化するとこちらです。

\( \ \log \ \)の右下の小さい数値を底(てい),\( \ \log \ \)の隣の大きな数値を真数(しんすう)といいます。
読み方は,\( \ \log_{10}1 \ 000 \ \)であれば“ログ\( \ 10 \ \)の\( \ 1 \ 000 \ \)”,“ログ\( \ 10 \ \)てい\( \ 1 \ 000 \ \)”,あるいは文脈で底が\( \ 10 \ \)であることが明らかであれば省略されて”ログ\( \ 1 \ 000 \ \)”です。
【練習問題】
\( \ \log \ \)の形に書き換えましょう。
\( (1) \) \( \ 2^{3}=8 \ \)
\( (2) \) \( \ 5^{2}=25 \ \)
\( (3) \) \( \ 3^{-2}=\displaystyle \frac {1}{9} \ \)
\( (4) \) \( \ 10^{x}=y \ \)
\( (1) \) \( \ \log_{2}8=3 \ \)
\( (2) \) \( \ \log_{5}25=2 \ \)
\( (3) \) \( \ \displaystyle \log_{3}\frac {1}{9}=-2 \ \)
\( (4) \) \( \ \displaystyle \log_{10}y=x \ \)
次の値を求めましょう。
\( (5) \) \( \ \log_{2}32 \ \)
\( (6) \) \( \ \log_{3}27 \ \)
\( (7) \) \( \ \log_{7}\displaystyle \frac {1}{49} \ \)
\( (5) \)
\( \ \log_{2}32=x \ \)とおく。
指数に書き換えると,
\[
\begin{eqnarray}
2^{x}&=&32 \\[ 5pt ]
\end{eqnarray}
\]
より,\( \ x=5 \ \)
\( (6) \)
\( \ \log_{3}27=x \ \)とおく。
指数に書き換えると,
\[
\begin{eqnarray}
3^{x}&=&27 \\[ 5pt ]
\end{eqnarray}
\]
より,\( \ x=3 \ \)
\( (7) \)
\( \ \log_{7}\displaystyle \frac {1}{49}=x \ \)とおく。
指数に書き換えると,
\[
\begin{eqnarray}
7^{x}&=&\frac {1}{49} \\[ 5pt ]
\end{eqnarray}
\]
より,\( \ x=-2 \ \)
\( \ x \ \)がいくつか求めましょう。
\( (8) \) \( \ \log_{10}x=2 \ \)
\( (9) \) \( \ \log_{10}x=-3 \ \)
\( (8) \)
指数に書き換えると
\[
\begin{eqnarray}
10^{2}&=&x \\[ 5pt ]
\end{eqnarray}
\]
なので,\( \ x=100 \ \)
\( (9) \)
指数に書き換えると
\[
\begin{eqnarray}
10^{-3}&=&x \\[ 5pt ]
\end{eqnarray}
\]
なので,\( \ x=0.001 \ \)または\( \ x=\displaystyle \frac {1}{1 \ 000} \ \)
電験に必要なのは常用対数\( \ \log_{10} \ \)
底が\( \ 10 \ \)の対数,つまり\( \ \log_{10} \ \)を“常用対数”と呼び,その名の通り非常によく用いられます。
\( \ \log_{10} \ \)の\( \ 10 \ \)は省略されることがあります。つまり\( \ \log 1 \ 000 \ \)とは,\( \ \log_{10}1 \ 000 \ \)のことです。
電験\( \ 3 \ \)種の出題は,ほぼすべて\( \ \log_{10} \ \)です。したがってこの解説でも\( \ \log_{10} \ \)を扱います。
\( \ \log \ \)の後ろの大きな数字は,真数というのですが,この解説では直観的な分かりやすさを重視して,\( \ \log \ \)の“中身”と呼びます。もちろん数学用語ではないのでご注意ください。


