【対数③】何乗したら 1 になる？納得のたとえ話―（イ）log1 ，（オ）の解説―

何乗したら\( \ 1 \ \)になる？納得のたとえ話―（イ）\( \ \log _{10}1 \ \)，（オ）の解説―

こちらがいくつか，分かるでしょうか？
\[
\begin{eqnarray}
\log _{10}1 \\[ 5pt ] \end{eqnarray}
\] “\( \ 10 \ \)を\( \ 1 \ \)にするには何乗したらよいか”ですね。直観的に分かる人は少ないでしょう。

指数では“\( \ 0 \ \)乗すると\( \ 1 \ \)”という言葉があり，あらゆる数字が\( \ 0 \ \)乗すると\( \ 1 \ \)になります。
したがって，\( \ 10^{0}=1 \ \)より，
\[
\begin{eqnarray}
\log _{10}1=\log _{10}10^{0}=0 \\[ 5pt ] \end{eqnarray}
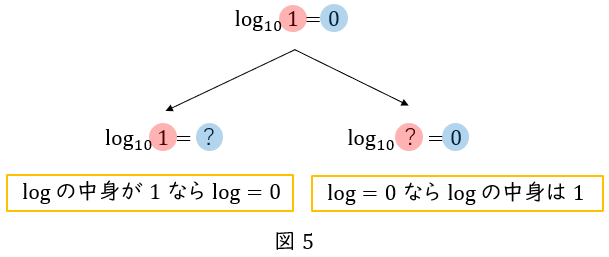
\] となります。

逆に，\( \ \log _{10}〇=0 \ \)の場合は，\( \ 〇=1 \ \)です。

なぜ“\( \ 0 \ \)乗すると\( \ 1 \ \)”なのか

\( \ 10 \ \)を\( \ 0 \ \)回かけ算する，つまり\( \ 1 \ \)回もかけ算しないのだから，\( \ 10^{0}=0 \ \)なのでは？と思う方もいるでしょう。
しかし実際は，あらゆる数字において“\( \ 0 \ \)乗すると\( \ 1 \ \)”です。なぜでしょうか。
簡単にいえば，計算に都合がいいよう\( \ 0 \ \)乗を\( \ 1 \ \)と定義したのです。

例えば\( \ 10^{x} \ \)の\( \ x \ \)を\( \ 1 \ \)ずつ減らして並べてみましょう。

指数の\( \ x \ \)が\( \ 1 \ \)減ると，\( \ 10^{x} \ \)は\( \ \displaystyle \frac {1}{10} \ \)倍になります。

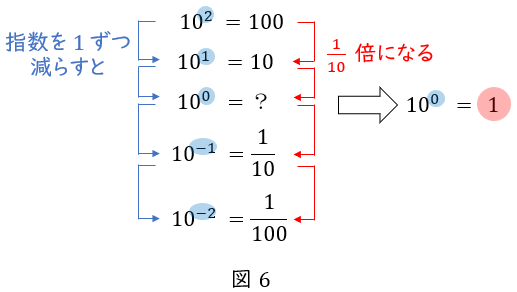
これが，\( \ 10^{0} \ \)の所でも成り立ってほしいので，\( \ 10^{0}=1 \ \)としているのです。

\( \ 10^{x} \ \)以外でも同様です。例えば\( \ 2^{x} \ \)の場合は，\( \ x \ \)が\( \ 1 \ \)減ると，\( \ 2^{x} \ \)は\( \ \displaystyle \frac {1}{2} \ \)倍になります。

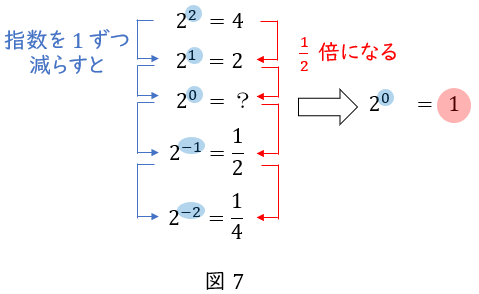
これが\( \ 2^{0} \ \)でも成り立ってほしいので，\( \ 2^{0}=1 \ \)としているのです。

したがって，\( \ 10^{0} \ \)がいくつか分からない場合は\( \ 10^{2}=100 \ \)，\( \ 10^{1}=10 \ \)と，実際に書いてみましょう。

“\( \ 0 \ \)乗すると\( \ 1 \ \)”を理解できるたとえ話

もっとイメージで捉えたい方に，こんなお話はいかがでしょうか。

ある人が風邪をひきました。\( \ 1 \ \)日で\( \ 10 \ \)人にうつして治ったとします。今，風邪をひいているのは\( \ 10 \ \)人です。
\( \ 1 \ \)日目，その\( \ 10 \ \)人が，それぞれ\( \ 10 \ \)人にうつして治ったとします。今，風邪をひいているのは\( \ 100 \ \)人です。
\( \ 2 \ \)日目，その\( \ 100 \ \)人が，それぞれ\( \ 10 \ \)人に風邪をうつして…
…なんとも嫌な話ですね。

このとき，\( \ n \ \)日目に風邪をひいているのは\( \ 10^{n} \ \)人です。
そして初日（\( \ 0 \ \)日目）には，最初に風邪をひいた\( \ 1 \ \)人がいます。したがって，\( \ 10^{0}=1 \ \)となります。

【練習問題】

\( (1) \)　\( \ \log _{a}1 \ \)（ただし，\( \ a≠0 \ \)とする）はいくつか

\( (2) \)　\( \ \log _{10}\displaystyle \frac {K}{\omega T}=0 \ \)のとき，\( \ \displaystyle \frac {K}{\omega T} \ \)はいくつか