【対数④】対数公式の証明とその使い方―（ウ）log⁡12 の解説―

(1)　かけ算は足し算に
\( \ \log_{10} \ \)の中身がかけ算なら，足し算に分解できます
\[
\begin{eqnarray}
\log_{10}⁡XY&=&\log_{10}⁡X+\log_{10}⁡Y \\[ 5pt ] \end{eqnarray}
\]

証明
\( \ \log_{10}⁡X=a \ \)とします。これは“\( \ 10 \ \)を\( \ X \ \)にするには\( \ a \ \)乗すればよい”という意味ですから，
\[
\begin{eqnarray}
10^{a}&=&X \\[ 5pt ] \end{eqnarray}
\] となります。
同様に，\( \ \log_{10}Y=b \ \)とします。これは，“\( \ 10 \ \)を\( \ Y \ \)にするには\( \ b \ \)乗すればよい”という意味ですから，
\[
\begin{eqnarray}
10^{b}&=&Y \\[ 5pt ] \end{eqnarray}
\] となります。
これから，\( \ \log_{10}⁡XY=\log_{10}⁡X+\log_{10}⁡Y \ \)を証明するために，左辺の\( \ \log_{10}⁡XY \ \)を計算するのですが，まずは中身の\( \ ⁡XY \ \)だけを計算します。

したがって，\( \ \log_{10}⁡XY \ \)は，
\[
\begin{eqnarray}
\log_{10}⁡XY&=&\log_{10}10^{\left( a+b\right) } \\[ 5pt ] \end{eqnarray}
\] 右辺は，“\( \ 10 \ \)を\( \ 10 \ \)の\( \ a+b \ \)乗にするには何乗したらよいか”ですので，\( \ a+b \ \)です。
\[
\begin{eqnarray}
\log_{10}⁡XY&=&\log_{10}10^{\left( a+b\right) }=a+b \\[ 5pt ] \end{eqnarray}
\] \( \ a \ \)，\( \ b \ \)は，\( \ \log_{10}⁡X=a \ \)，\( \ \log_{10}⁡Y=b \ \)ですから，
\[
\begin{eqnarray}
\log_{10}⁡XY&=&\log_{10}10^{\left( a+b\right) }=a+b=\log_{10}⁡X+\log_{10}⁡Y \\[ 5pt ] \end{eqnarray}
\] 以上より，
\[
\begin{eqnarray}
\log_{10}⁡XY&=&\log_{10}⁡X+\log_{10}⁡Y \\[ 5pt ] \end{eqnarray}
\] となります。

(2)　わり算は引き算に
\( \ \log_{10} \ \)の中身がわり算なら，引き算に分解できます
\[
\begin{eqnarray}
\log_{10}\frac {⁡X}{Y}&=&\log_{10}⁡X-\log_{10}⁡Y \\[ 5pt ] \end{eqnarray}
\]

証明
(1)と同様に証明できます。\( \ \log_{10}⁡X=a \ \)および\( \ \log_{10}⁡Y=b \ \)とすると，\( \ 10^{a}=X \ \)および\( \ 10^{b}=Y \ \)です。
これから，\( \ \displaystyle \log_{10}\frac {X}{Y}=\log_{10}⁡X-\log_{10}⁡Y \ \)を証明するために，左辺の\( \ \displaystyle \log_{10}\frac {X}{Y} \ \)を計算するのですが，まず中身の\( \ \displaystyle \frac {X}{Y} \ \)だけを計算します。

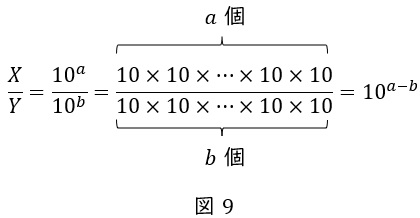
したがって，\( \ \displaystyle \log_{10}\frac {X}{Y} \ \)は，
\[
\begin{eqnarray}
\log_{10}\frac {⁡X}{Y}&=&\log_{10}10^{a-b} \\[ 5pt ] \end{eqnarray}
\] 右辺は，“\( \ 10 \ \)を\( \ 10 \ \)の\( \ a-b \ \)乗にするには何乗したらよいか”ですので，\( \ a-b \ \)です。
\[
\begin{eqnarray}
\log_{10}\frac {⁡X}{Y}&=&\log_{10}10^{a-b}=a-b \\[ 5pt ] \end{eqnarray}
\] \( \ a \ \)，\( \ b \ \)は，\( \ \log_{10}⁡X=a \ \)，\( \ \log_{10}⁡Y=b \ \)ですから，
\[
\begin{eqnarray}
\log_{10}\frac {⁡X}{Y}&=&\log_{10}10^{a-b}=a-b=\log_{10}⁡X-\log_{10}⁡Y \\[ 5pt ] \end{eqnarray}
\] 以上より，
\[
\begin{eqnarray}
\log_{10}\frac {⁡X}{Y}&=&\log_{10}⁡X-\log_{10}⁡Y \\[ 5pt ] \end{eqnarray}
\] となります。

(3)　指数は\( \ \log \ \)の前に出せる
\( \ \log_{10}⁡ \ \)の中身が指数なら，前に出してかけ算にすることができます。
\[
\begin{eqnarray}
\log_{10}X^{n}&=&n\log_{10}⁡X \\[ 5pt ] \end{eqnarray}
\]

証明
(1)\( \ \log_{10}⁡XY=\log_{10}⁡X+\log_{10}⁡Y \ \)を使って簡単に証明できます。
かけ算は足し算に分解できるので，

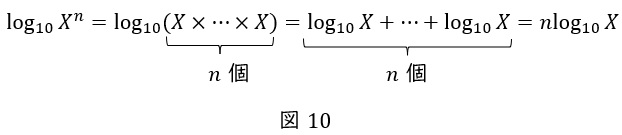
つまり，\( \ \log_{10} X \ \)を\( \ n \ \)回足し算するので，\( \ n \log_{10} X \ \)となります。
実をいうと，先に出てきた\( \ \log_{10}⁡10^{x}=x \ \)も，こちらの公式を利用しています。
指数は前に出せるので，
\[
\begin{eqnarray}
\log_{10}10^{x}&=&x\log_{10}⁡10 \\[ 5pt ] \end{eqnarray}
\] そして\( \ \log_{10}⁡10 \ \)とは，“\( \ 10 \ \)を\( \ 10 \ \)にするためには何乗すればよいか” ですから，\( \ \log_{10}⁡10=1 \ \)です。
したがって，
\[
\begin{eqnarray}
\log_{10}10^{x}&=&x\log_{10}⁡10=x \\[ 5pt ] \end{eqnarray}
\] となります。

まず，\( \ \log_{10}⁡1 \ \)，\( \ \log_{10}⁡10 \ \)を記入します。
次に，\( \ \log_{10}⁡n \ \)の\( \ n \ \)を，\( \ 2 \ \)，\( \ 3 \ \)，\( \ 7 \ \)，\( \ 10 \ \)を使ったかけ算・わり算の形にします。
最後に，公式を使って\( \ \log_{10}⁡n \ \)を計算します。

\[
\begin{array}{|c|c|c|l|}
\hline
\log _{10}n & & n & 　　　公式で \ \log_{10}⁡n \ を書き換える \\
\hline
\log _{10}1 & \color {red}{0} & & \\
\hline
\log _{10}2 & 0.301 & & \\
\hline
\log _{10}3 & 0.477 & & \\
\hline
\log _{10}4 & \color {red}{0.602} & 4=2^{2} & \log_{10}4=\log_{10}2^{2}=2\log_{10}2=0.602 \\
\hline
\log _{10}5 & \color {red}{0.699} & \displaystyle 5=\frac {10}{2} & \displaystyle \log_{10}5=\log_{10}\frac {10}{2}=\log_{10}10-\log_{10}2=0.699 \\
\hline
\log _{10}6 & \color {red}{0.778} & 6=2\times 3 & \log_{10}6=\log_{10}2+\log_{10}3=0.778 \\
\hline
\log _{10}7 & 0.845 & & \\
\hline
\log _{10}8 & \color {red}{0.903} & 8=2^{3} & \log_{10}8=\log_{10}2^{3}=3\log_{10}2=0.903 \\
\hline
\log _{10}9 & \color {red}{0.954} & 9=3^{2} & \log_{10}9=\log_{10}3^{2}=2\log_{10}3=0.954 \\
\hline
\log _{10}10 & \color {red}{1} & & \\
\hline
\end{array}
\]

\( \ \log_{10} \ \)の中身が，\( \ 2 \ \)，\( \ 3 \ \)，\( \ 7 \ \)そして\( \ 10 \ \)を使って表せるはずです。

\( (1) \)　
\( \ \displaystyle 2.1=\frac {21}{10}=\frac {3\times 7}{10} \ \)なので，
\[
\begin{eqnarray}
\log_{10}⁡2.1&=&\log_{10}\frac {3\times 7}{10} \\[ 5pt ] &=&\log_{10}3+\log_{10}7-\log_{10}10 \\[ 5pt ] &=&0.477+0.845-1 \\[ 5pt ] &=&0.322 \\[ 5pt ] \end{eqnarray}
\]

\( (2) \)
\( \ \displaystyle 3.5=\frac {7}{2} \ \)なので，
\[
\begin{eqnarray}
\log_{10}⁡3.5&=&\log_{10}\frac {7}{2} \\[ 5pt ] &=&\log_{10}7-\log_{10}2 \\[ 5pt ] &=&0.845-0.301 \\[ 5pt ] &=&0.544 \\[ 5pt ] \end{eqnarray}
\]

\( (3) \)
\( \ \displaystyle 45=9\times 5=3^{2}\times \frac {10}{2} \ \)なので，
\[
\begin{eqnarray}
\log_{10}⁡45&=&\log_{10}\left( 3^{2}\times \frac {10}{2}\right) \\[ 5pt ] &=&\log_{10}3^{2}+\log_{10}10-\log_{10}2 \\[ 5pt ] &=&2\log_{10}3+\log_{10}10-\log_{10}2 \\[ 5pt ] &=&2\times 0.477+1-0.301 \\[ 5pt ] &=&1.653 \\[ 5pt ] \end{eqnarray}
\]