【対数⑤】対数計算の王道手順の紹介　―（エ）計算ミスを防ぐ方法―

問15(b)は，下式に\( \ \omega =100 \ \)など数値を代入して解きます。
\[
\begin{eqnarray}
g&=&20\log_{10}\left| G\left( \mathrm {j}\omega \right) \right| \\[ 5pt ] &=&20\log_{10}\frac {1}{\sqrt {\left( 1-1\times 10^{-6}\omega ^{2}\right) ^{2}+\left( 1\times 10^{-4}\omega ^{2}\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] 私なりの計算のコツはこちらです。
・底の\( \ 10 \ \)は書きません。底なのか\( \ \log \ \)の中身の数字なのか混乱を避けるためです。
・\( \ 20\log_{10} \ \)，分数，\( \ \sqrt { \quad } \ \)を何度も書かないよう\( \ 〇 \ \)や\( \ □ \ \)にします。ゴチャゴチャしてミスの元だからです。
・\( \ 〇 \ \)や\( \ □ \ \)の定義は右上に書き，モコモコで目立たせます。\( \ 〇 \ \)や\( \ □ \ \)で計算を終えないようにするためです。
・\( \ 100 \ \)や\( \ 1 \ 000 \ \)ではなく，\( \ 10^{2} \ \)や\( \ 10^{3} \ \)の形で代入します。\( \ 0 \ \)の数を数えるのはミスの元だからです。
・“む” は ”無視する“ という意味です。どのような場合に無視するかは，この後すぐ説明します。
・無視した部分がある場合，\( \ = \ \)ではなく，\( \ ≃ \ \)と書きます。 “ほぼ等しい”という意味です。

“む”と書いて無視した部分についての解説です。
電験三種の問題形式（\( \ 5 \ \)択から適切なボード線図や式を選ぶ）においては，計算途中で\( \ 2 \ \)桁以上小さい数の足し算引き算を無視しても，計算結果に大差がなく，正しい選択肢に辿り着けます。
例えば前問の計算では，\( \ 1 \ \)と\( \ 1×10^{-2} \ \)との引き算において，\( \ 1×10^{-2} \ \)を無視しました。
これは，\( \ 1×10^{-2} \ \)つまり\( \ 0.01 \ \)が\( \ 1 \ \)に比べて\( \ 2 \ \)桁以上小さいためです。
\[
\begin{eqnarray}
1-1×10^{-2}&≃&1 \\[ 5pt ] \end{eqnarray}
\] 大切なことなので繰り返します。
\( \ 1×10^{-2} \ \)とそのものが小さい数字かどうかではなく，足し算・引き算する相手に比べて，\( \ 2 \ \)桁以上小さいかどうかです。

この基準を踏まえて，前問の計算をもう一度確認しましょう。\( \ 2 \ \)か所で無視をしています。

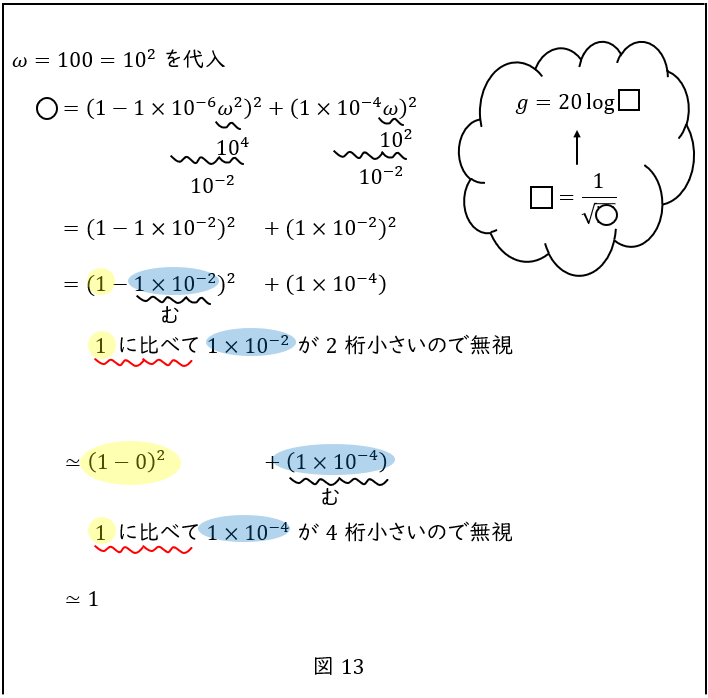
注意点として，無視する数字が前に来る場合もあります。
\[
\begin{eqnarray}
-1×10^{-2}+1&≃&1 \\[ 5pt ] \end{eqnarray}
\] また，\( \ 1 \ \)以上の数字が無視できる場合もあります。
\[
\begin{eqnarray}
1+1×10^{2}&≃&1×10^{2} \\[ 5pt ] \end{eqnarray}
\] なお，ここまでの説明を聞いて，無視できるか判断する自信がない，と思った方も大丈夫です。分からない場合は普通に計算してください。例えば前問はこうなります。

\( \ \sqrt {0.980 \ 2} \ \)が出てきたところで，およそ\( \ 1 \ \)であることに気がつけると思います。

【練習問題】（令和４年下期機械科目問15より）

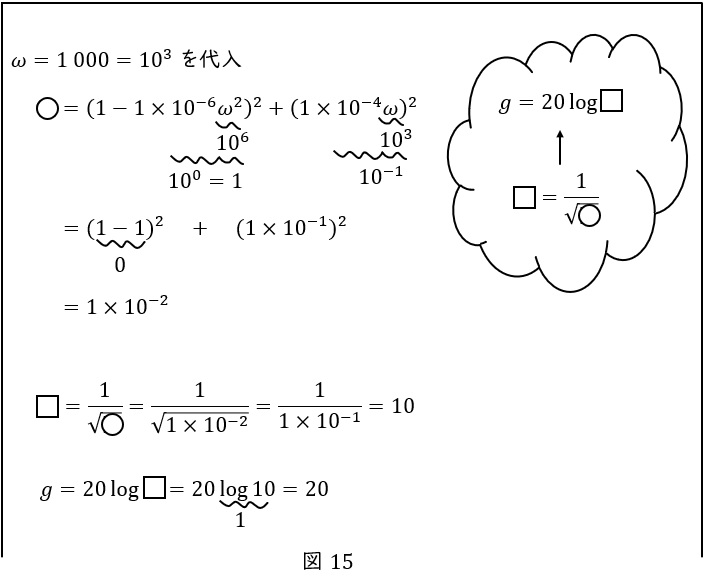
\( \ \omega =1 \ 000 \ \)の場合，および\( \ \omega =10 \ 000 \ \)の場合の，\( \ \displaystyle g=20\log_{10}\frac {1}{\sqrt {\left( 1-1\times 10^{-6}\omega ^{2}\right) ^{2}+\left( 1\times 10^{-4}\omega ^{2}\right) ^{2}}} \ \)の値を計算してください。

令和５年下期機械科目問13では，ゲインの式がこのようになります。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {K}{\sqrt {K^{2}+\left( \omega T\right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] \( \ 〇 ^{2}+□ ^{2} \ \)の形が出てきたら，\( \ \omega \ \)の大小で場合分けです。

\( \ \underline {\omega } \ \)が十分に小さいとき
\( \ \left( \omega T\right) ^{2} \ \)も小さくなるため，\( \ K^{2} \ \)に比べて\( \ \left( \omega T\right) ^{2} \ \)は十分小さいとして無視できます。
\( \ \sqrt {K^{2}+\left( \omega T\right) ^{2}}≃\sqrt {K^{2}}=K \ \)となります。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {K}{\sqrt {K^{2}+\left( \omega T\right) ^{2}}} \\[ 5pt ] &≃&20\log_{10}\frac {K}{K} \\[ 5pt ] &=&20\log_{10}1 \\[ 5pt ] &=&20\times 0 \\[ 5pt ] &=& 0 \\[ 5pt ] \end{eqnarray}
\]

\( \ \underline {\omega } \ \)が十分に大きいとき
\( \ \left( \omega T\right) ^{2} \ \)もとても大きくなるため，\( \ \left( \omega T\right) ^{2} \ \)に比べて\( \ K^{2} \ \)は十分小さいとして無視できます。
\( \ \sqrt {K^{2}+\left( \omega T\right) ^{2}}≃\sqrt {\left( \omega T\right) ^{2}}=\omega T \ \)となります。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {K}{\sqrt {K^{2}+\left( \omega T\right) ^{2}}} \\[ 5pt ] &≃&20\log_{10}\frac {K}{\omega T} \\[ 5pt ] &=&20\log_{10}K-20\log_{10}\omega T \\[ 5pt ] \end{eqnarray}
\]

このように，\( \ 〇 ^{2}+□ ^{2} \ \)の形が出てきたら，\( \ \omega \ \)の大小で場合分けをすることで，分母のルートを外すことができます。

また，\( \ 1+□ ^{2} \ \)の形が出てきた場合も同様に\( \ \omega \ \)の大小で場合分けです。\( \ 〇 ^{2}+□ ^{2} \ \)の\( \ 〇=1 \ \)ということですね。

【練習問題】（令和３年機械科目問13より）

令和３年機械科目問13では，ゲインの式がこうなります。\( \ \omega \ \)の大小で場合分けをしてみましょう。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {1}{\sqrt {1+\left( 0.01\omega \right) ^{2}}} \\[ 5pt ] \end{eqnarray}
\]