Contents
対数座標の見方とボード線図の問題の解き方の王道―(カ)対数座標,ボード線図―
ボード線図とは,角周波数\( \ \omega \ \)を変化させた場合のゲイン\( \ g \ \)の変化を表す図です。
ゲインは,以下の式で表されます。
\[
\begin{eqnarray}
g&=&20\log_{10}\left| W\left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
\end{eqnarray}
\]
ポイントは,“\( \ \omega \ \)が広範囲で変化する(桁が大きく変わる)”ということです。
対数座標とは
ボード線図では対数座標が使用されます。“座標”が堅苦しければ,“目盛り”と考えてください。ここでは,対数目盛りについて,普通の目盛り(均等目盛りといいます)と比較しながら説明します。
対数目盛りの定義
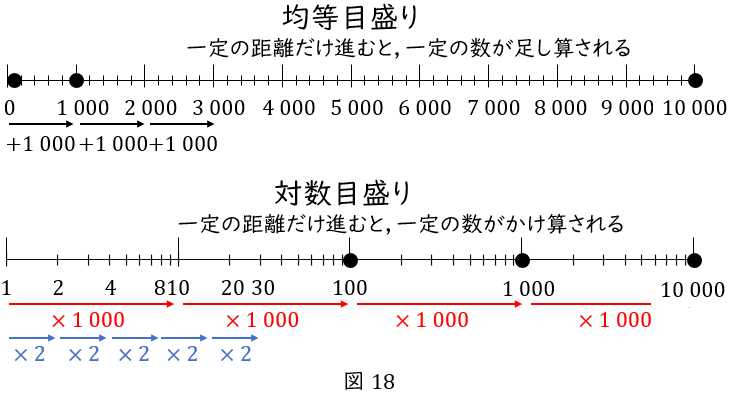
普通の目盛りは,一定の距離だけ進むと一定の数が“足し算”される目盛りです。均等目盛りといいます。
一方,対数目盛りは,一定の距離だけ進むと一定の数が“かけ算”される目盛りです。
例えば,赤の矢印だけ進むと,\( \ 1 \ \),\( \ 10 \ \),\( \ 100 \ \),\( \ 1 \ 000 \ \),\( \ 10 \ 000 \ \)のように,\( \ 10 \ \)倍になります。
また,青の矢印だけ進むと,\( \ 1 \ \),\( \ 2 \ \),\( \ 4 \ \),\( \ 8 \ \),\( \ 16 \ \),\( \ 32 \ \cdots \)のように,\( \ 2 \ \)倍になります。
対数目盛りのメリット
図18には,\( \ 100 \ \),\( \ 1 \ 000 \ \),\( \ 10 \ 000 \ \)がプロットしてあります。均等目盛りでは,\( \ 100 \ \)のプロットがつぶれて,読み取りにくくなっています。一方,対数目盛りでは,桁の小さい数値もつぶれず見やすくなっています。したがって対数目盛りは,桁が大きく変化する数値を表すのに適しています。
対数目盛りの最小値
図18では対数目盛りの左端(最小値)を\( \ 1 \ \)にしましたが,\( \ 100 \ \)でも\( \ 0.001 \ \)でも構いません。ただし,\( \ 0 \ \)は対数目盛りに存在しません。\( \ 0 \ \)に何をかけ算しても\( \ 0 \ \)ですから,もし対数目盛りに\( \ 0 \ \)が存在してしまうと,すべての目盛りが\( \ 0 \ \)になってしまうからです。
ところが,大変ややこしいことに,計算上は対数目盛りに\( \ 0 \ \)が存在するかのように扱うことがあります。これについては,実際に問題を解きながら解説した方が分かりやすいので,練習問題にて解説します。
ボード線図の問題の解き方
電験でのボード線図の出題は,複数のボード線図から正しいものを選ぶ形式や,ボード線図が言葉で説明されており,空欄の言葉や数字を埋める形式です。
そして重要なことは,“\( \ \omega \ \)が広い範囲で変化する(桁が大きく変わる)”ということです
解き方の手順はこちらです。
・数値があれば代入
・数値がなければ\( \ \omega \ \)の大小で場合分け
縦軸と横軸に数値があるので,実際に代入して解きます。
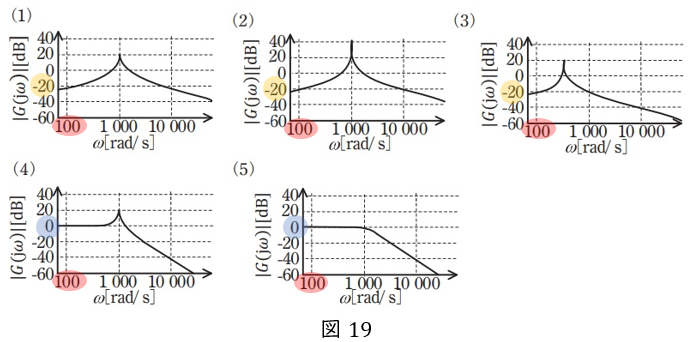
\( \ \omega =100 \ \)を代入して,ゲインがおよそ\( \ -20 \ \)であれば正答は(1)か(2)か(3)であり,\( \ 0 \ \)であれば(4)か(5)です。
ゲインの式は次の通りです。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {1}{\sqrt {\left( 1-1\times 10^{-6}\omega ^{2}\right) ^{2}+\left( 1\times 10^{-4}\omega ^{2}\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
ここに\( \ \omega =100 \ \)を代入すると,\( \ g=0 \ \)となります(計算の詳細は対数⑤をご覧ください)。したがって答えは(4)か(5)です。
次に,(4)と(5)が,どこが違うかを見比べます。
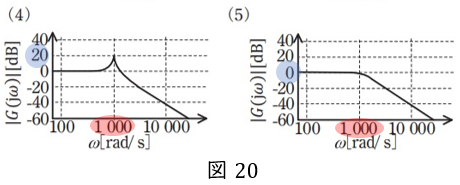
\( \ \omega =1 \ 000 \ \)のとき,\( \ 20 \ \)なら正答は(4),\( \ 0 \ \)なら(5)です。
なお,\( \ \omega =10 \ 000 \ \)のときは,(4)も(5)もおよそ\( \ -40 \ \)ですから,これで答えは絞り込めません。
ゲインの式に\( \ \omega =1 \ 000 \ \)を代入すると,\( \ g=20 \ \)です(計算の詳細は対数⑤をご覧ください)。
以上より,正答は(4)です。
軸に数値がありません。このような場合は\( \ \omega \ \)の大小で場合分けします。
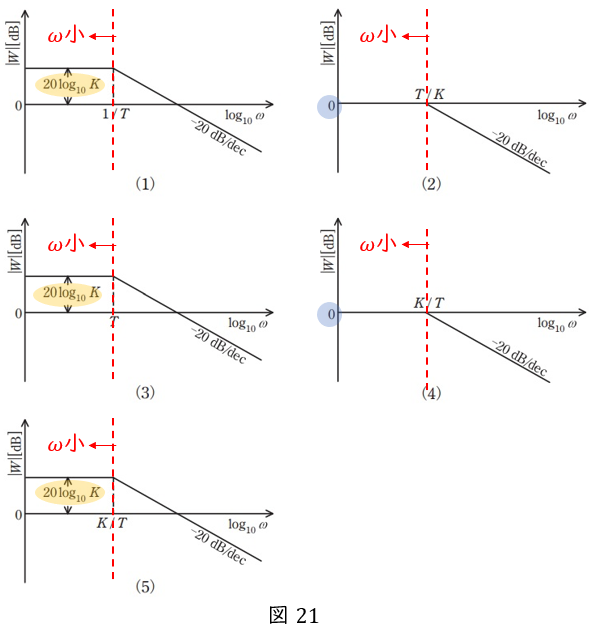
\( \ \underline {\omega } \ \)が小さいとき=横軸の左側
グラフを見ると,ゲイン(縦軸)が一定値になっていますね。\( \ 20 \log_{10} K \ \)なら正答は(1),(3),(5)のいずれか,\( \ 0 \ \)なら(2),(4)のいずれかです。
この問題で,ゲインは以下の式で表されます。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {K}{\sqrt {K^{2}+\left( \omega T\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \omega \ \)が小さいとき,\( \ \left( \omega T\right) ^{2} \ \)も小さくなるため,\( \ K^{2} \ \)に比べて\( \ \left( \omega T\right) ^{2} \ \)は十分小さいとして無視できます。
\( \ \sqrt {K^{2}+\left( \omega T\right) ^{2}}≃\sqrt {K^{2}}=K \ \)なので,
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {K}{K} \\[ 5pt ]
&=&20\log_{10}1 \\[ 5pt ]
&=&20\times 0 \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
したがって,答えは(2),(4)のいずれかです。
\( \ \underline {\omega } \ \)が大きいとき=横軸の右側
グラフは右下がりの直線です。一定値だったグラフが折れ曲がる点が,\( \ T/K \ \)なら正答は(2),\( \ K/T \ \)なら(4)です。
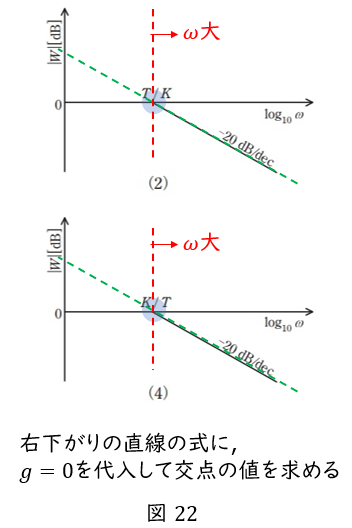
折れ曲がる点とは,右下がりの直線と横軸の交点です。したがって,右下がりの直線の式を求めて,\( \ g=0 \ \)を代入して,交点の値を求めます。
まずは右下がりの直線の式を導出しましょう。
\[
\begin{eqnarray}
g&=&20\log_{10}\frac {K}{\sqrt {K^{2}+\left( \omega T\right) ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \omega \ \)が大きいとき,\( \ \left( \omega T\right) ^{2} \ \)も大きくなるため,\( \ \left( \omega T\right) ^{2} \ \)に比べて\( \ K^{2} \ \)は十分小さいとして無視できます。
\( \ \sqrt {K^{2}+\left( \omega T\right) ^{2}}≃\sqrt { \left( \omega T\right) ^{2}}=\omega T \ \)なので,
\[
\begin{eqnarray}
g&≃&20\log_{10}\frac {K}{\omega T} \\[ 5pt ]
\end{eqnarray}
\]
この時点では,右下がりの直線の式に見えません。横軸が\( \ \log_{10} \omega \ \)ですから,この形を目指します。
\[
\begin{eqnarray}
g&=&〇\times \log_{10}\omega +□ \\[ 5pt ]
\end{eqnarray}
\]
したがって,分母の\( \ \omega \ \)を引き算に分解して,
\[
\begin{eqnarray}
g&≃&20\log_{10}\frac {K}{\omega T} \\[ 5pt ]
&=&20\log_{10}\frac {K}{T}-20\log_{10}\omega \\[ 5pt ]
&=&-20\log_{10}\omega +20\log_{10}\frac {K}{T} \\[ 5pt ]
\end{eqnarray}
\]
無事に右下がりの直線の形になりました。傾きは\( \ -20 \ \)です。実際グラフにも,傾きが\( \ -20 \ \)と書いてありますね。
ここに,\( \ g=0 \ \)を代入します。
\[
\begin{eqnarray}
0&=&-20\log_{10}\omega +20\log_{10}\frac {K}{T} \\[ 5pt ]
20\log_{10}\omega &=&20\log_{10}\frac {K}{T} \\[ 5pt ]
\log_{10}\omega &=&\log_{10}\frac {K}{T} \\[ 5pt ]
\omega &=&\frac {K}{T} \\[ 5pt ]
\end{eqnarray}
\]
よって,正答は (4)です。
【練習問題\( \ \mathrm {A} \ \)】(令和2年機械科目問17より)
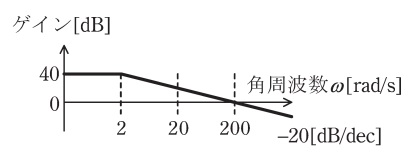
(a) 図のゲイン特性を示す周波数伝達関数として,最も適切なものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{eqnarray}
&(1)& \ \displaystyle \frac {40}{1+\mathrm {j}\omega } \ &(2)& \ \displaystyle \frac {40}{1+\mathrm {j}0.005\omega } \ &(3)& \ \displaystyle \frac {100}{1+\mathrm {j}\omega } \ \\[ 5pt ]
&(4)& \ \displaystyle \frac {100}{1+\mathrm {j}0.005\omega } \ &(5)& \ \displaystyle \frac {100}{1+\mathrm {j}0.5\omega } \ && \\[ 5pt ]
\end{eqnarray}
\]
複数のボード線図から正しいものを選ぶ問題が定番ですが,この問題はその逆です。ボード線図が与えられており,複数の周波数伝達関数の中から,正しいものを選びます。
この問題は 2 つの注意点があります。
注意点1:折れ曲がった部分に近似が使われている場合は代入しない
この問題は,ボード線図に具体的な数値があるので,これを(1)~(5)に代入して解きます。
ボード線図によると\( \ \omega =2 \ \)のときゲインが\( \ 40 \ \)ですが,\( \ \omega =2 \ \)を代入するのはおすすめしません。ボード線図は通常折線近似が使われており,特に折れ曲がり部分には大胆な近似が使われているからです。つまり,\( \ \omega =2 \ \)のときゲインが\( \ 40 \ \)やそれに近い数値にはならないのです。
代入する\( \ \omega \ \)は,できるだけ小さい数値と大きい数値を選びましょう。実際に問題を解くと分かるのですが,\( \ \omega \ \)の大小で場合分けすることで,小さい数値を無視して式を簡単にできるからです。
注意点2:周波数伝達関数≠ゲイン
(1)~(5)は周波数伝達関数であり,ボード線図の縦軸はゲインです。これらを混同しないようにしましょう。
(1)を例にとると,周波数伝達関数とゲインの関係はこのようになります。

注意点が分かったところで,実際に解いてみましょう。まずは\( \ \omega =0 \ \)を代入します。
ここで,注意深い受験生は疑問に思うかもしれません。今回の横軸\( \ \left( \omega \right) \ \)は\( \ 2 \ \),\( \ 20 \ \),\( \ 200 \ \)とあるので,横軸の左端は\( \ 0.2 \ \)から始まっているように見えますし,そもそも対数座標の説明で述べた通り,対数座標に\( \ 0 \ \)は存在しません。
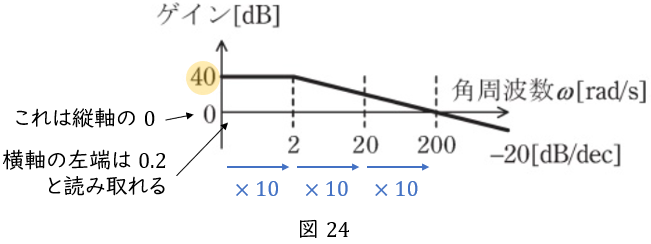
\( \ \underline {\omega =0} \ \)を代入してよい理由
グラフに存在しない\( \ \omega =0 \ \)を代入していいのか,という疑問は素晴らしいのですが,実際は問題ありません。問題がないどころか,短時間で正解候補を絞り込めるので,電験合格には必須の技となります。
\( \ \omega =0 \ \)を代入して問題ない理由を説明します。ボード線図は,\( \ \omega \ \)(横軸)が\( \ 2 \ \)以下のとき,ゲイン(縦軸)が一定値となっています。つまり,\( \ \omega \ \)が\( \ 2 \ \)以下の場合は,\( \ \omega \ \)の値は関係ないのです。ということは,ゲインの式には\( \ \omega \ \)が存在しない,つまり分母にある\( \ 1+\mathrm {j}〇\omega \ \)の,\( \ \mathrm {j}〇\omega \ \)は無視されたということです。したがって,\( \ \omega =0 \ \)を代入して問題ありません。どうしても抵抗がある方は,\( \ \omega =0.000 \ 001 \ \)などの値を代入して,足し算する相手\( \ \left( 1\right) \ \)に比べて\( \ 2 \ \)桁以上小さいので無視・・・と考えるとよいでしょう。
\( \ \underline {\omega =0} \ \)を代入
では,まずは(1)に\( \ \omega =0 \ \)を代入しましょう。ゲインが\( \ 40 \ \)なら,正答候補です。
\( \ \omega =0 \ \)なら分母が\( \ 1 \ \)なので,周波数伝達関数は\( \ 40 \ \)です。ゲインに変換すると\( \ 20 \log 40 \ \)です。\( \ \log 40 \ \)がいくつかは,分かりませんが,\( \ 2 \ \)でないことは確かです。なぜなら\( \ \log 100=2 \ \)ですから。したがって,ゲインが 40 ではないので,(1)は正答ではないと分かります。

同様に(2)~(5)も計算すると以下の通りです。正答候補は(3)~(5)に絞られました。

ゲイン\( \ \underline {=0} \ \)を代入
続いて,\( \ \omega =200 \ \)のときにゲインが\( \ 0 \ \)という情報を使いましょう。
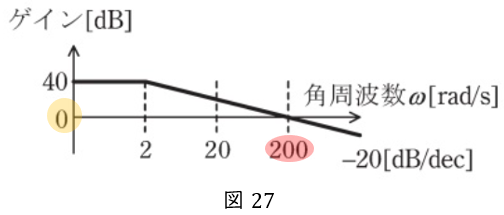
\( \ \omega =0 \ \)を代入した時にお分かりいただけたと思うのですが,代入する値が\( \ 0 \ \)なら計算が楽です。したがって,今回はゲインに\( \ 0 \ \)を代入するところからスタートしましょう。
まずは (3) を検討します。周波数伝達関数がこちらです。
\[
\begin{eqnarray}
\frac {100}{1+\mathrm {j}\omega } \\[ 5pt ]
\end{eqnarray}
\]
ゲインの式はこのようになります。
\[
\begin{eqnarray}
20\log \frac {100}{\sqrt {1+\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
これが\( \ 0 \ \)ですから,
\[
\begin{eqnarray}
20\log \frac {100}{\sqrt {1+\omega ^{2}}}=0 \\[ 5pt ]
\end{eqnarray}
\]
したがって,
\[
\begin{eqnarray}
\log \frac {100}{\sqrt {1+\omega ^{2}}}=0 \\[ 5pt ]
\end{eqnarray}
\]
\( \ \log=0 \ \)ということは,\( \ \log \ \)の中身が\( \ 1 \ \)ですから(\( \ 0 \ \)乗すると\( \ 1 \ \)),
\[
\begin{eqnarray}
\frac {100}{\sqrt {1+\omega ^{2}}}=1 \\[ 5pt ]
\end{eqnarray}
\]
つまり,\( \ \omega =200 \ \)を代入して,この等式が成立すれば,(3)が正答ということです。
(4),(5)についても同様ですから,このようになります。

では,(3)~(5)に\( \ \omega =200 \ \)を代入しましょう。

“む”と書いたのは,無視するという意味です。\( \ 2 \ \)桁以上小さい足し算・引き算は無視しています。
以上より,正答は(5)です。
【練習問題\( \ \mathrm {B} \ \)】(平成27年機械科目問17より)
(b) 次のボード線図には,正確なゲイン特性を実線で,その折線近似ゲイン特性を破線で示し,横軸には特に折れ点角周波数の数値を示している。上記(a)の周波数伝達関数\( \ W(\mathrm {j}\omega ) \ \)のボード線図のゲイン特性として,正しいものを次の(1)~(5)のうちから一つ選べ。ただし,横軸は角周波数\( \ \omega \ \)の対数軸であり,\( \ -20 \ \mathrm{[dB/dec]} \ \)とは,\( \ \omega \ \)が10倍大きくなるに従って\( \ \left| W(\mathrm {j}\omega ) \right| \ \)が\( \ -20 \ \mathrm{dB} \ \)変化する傾きを示している。
図のゲイン特性を示す周波数伝達関数として,最も適切なものを次の(1)~(5)のうちから一つ選べ。
\[
\begin{eqnarray}
&(1)& \ \displaystyle \frac {40}{1+\mathrm {j}\omega } \ &(2)& \ \displaystyle \frac {40}{1+\mathrm {j}0.005\omega } \ &(3)& \ \displaystyle \frac {100}{1+\mathrm {j}\omega } \ \\[ 5pt ]
&(4)& \ \displaystyle \frac {100}{1+\mathrm {j}0.005\omega } \ &(5)& \ \displaystyle \frac {100}{1+\mathrm {j}0.5\omega } \ && \\[ 5pt ]
\end{eqnarray}
\]
複数のボード線図から正しいものを選ぶ問題が定番ですが,この問題はその逆です。ボード線図が与えられており,複数の周波数伝達関数の中から,正しいものを選びます。
この問題は 2 つの注意点があります。
注意点1:折れ曲がった部分に近似が使われている場合は代入しない
この問題は,ボード線図に具体的な数値があるので,これを(1)~(5)に代入して解きます。
ボード線図によると\( \ \omega =2 \ \)のときゲインが\( \ 40 \ \)ですが,\( \ \omega =2 \ \)を代入するのはおすすめしません。ボード線図は通常折線近似が使われており,特に折れ曲がり部分には大胆な近似が使われているからです。つまり,\( \ \omega =2 \ \)のときゲインが\( \ 40 \ \)やそれに近い数値にはならないのです。
代入する\( \ \omega \ \)は,できるだけ小さい数値と大きい数値を選びましょう。実際に問題を解くと分かるのですが,\( \ \omega \ \)の大小で場合分けすることで,小さい数値を無視して式を簡単にできるからです。
注意点2:周波数伝達関数≠ゲイン
(1)~(5)は周波数伝達関数であり,ボード線図の縦軸はゲインです。これらを混同しないようにしましょう。
(1)を例にとると,周波数伝達関数とゲインの関係はこのようになります。

注意点が分かったところで,実際に解いてみましょう。まずは\( \ \omega =0 \ \)を代入します。
ここで,注意深い受験生は疑問に思うかもしれません。今回の横軸\( \ \left( \omega \right) \ \)は\( \ 2 \ \),\( \ 20 \ \),\( \ 200 \ \)とあるので,横軸の左端は\( \ 0.2 \ \)から始まっているように見えますし,そもそも対数座標の説明で述べた通り,対数座標に\( \ 0 \ \)は存在しません。

\( \ \underline {\omega =0} \ \)を代入してよい理由
グラフに存在しない\( \ \omega =0 \ \)を代入していいのか,という疑問は素晴らしいのですが,実際は問題ありません。問題がないどころか,短時間で正解候補を絞り込めるので,電験合格には必須の技となります。
\( \ \omega =0 \ \)を代入して問題ない理由を説明します。ボード線図は,\( \ \omega \ \)(横軸)が\( \ 2 \ \)以下のとき,ゲイン(縦軸)が一定値となっています。つまり,\( \ \omega \ \)が\( \ 2 \ \)以下の場合は,\( \ \omega \ \)の値は関係ないのです。ということは,ゲインの式には\( \ \omega \ \)が存在しない,つまり分母にある\( \ 1+\mathrm {j}〇\omega \ \)の,\( \ \mathrm {j}〇\omega \ \)は無視されたということです。したがって,\( \ \omega =0 \ \)を代入して問題ありません。どうしても抵抗がある方は,\( \ \omega =0.000 \ 001 \ \)などの値を代入して,足し算する相手\( \ \left( \right) \ \)に比べて\( \ 2 \ \)桁以上小さいので無視・・・と考えるとよいでしょう。
\( \ \underline {\omega =0} \ \)を代入
では,まずは(1)に\( \ \omega =0 \ \)を代入しましょう。ゲインが\( \ 40 \ \)なら,正答候補です。
\( \ \omega =0 \ \)なら分母が\( \ 1 \ \)なので,周波数伝達関数は\( \ 40 \ \)です。ゲインに変換すると\( \ 20 \log 40 \ \)です。\( \ \log 40 \ \)がいくつかは,分かりませんが,\( \ 2 \ \)でないことは確かです。なぜなら\( \ \log 100=2 \ \)ですから。したがって,ゲインが 40 ではないので,(1)は正答ではないと分かります。

同様に(2)~(5)も計算すると以下の通りです。正答候補は(3)~(5)に絞られました。

ゲイン\( \ \underline {=0} \ \)を代入
続いて,\( \ \omega =200 \ \)のときにゲインが\( \ 0 \ \)という情報を使いましょう。

\( \ \omega =0 \ \)を代入した時にお分かりいただけたと思うのですが,代入する値が\( \ 0 \ \)なら計算が楽です。したがって,今回はゲインに\( \ 0 \ \)を代入するところからスタートしましょう。
まずは (3) を検討します。周波数伝達関数がこちらです。
\[
\begin{eqnarray}
\frac {100}{1+\mathrm {j}\omega } \\[ 5pt ]
\end{eqnarray}
\]
ゲインの式はこのようになります。
\[
\begin{eqnarray}
20\log \frac {100}{\sqrt {1+\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
これが\( \ 0 \ \)ですから,
\[
\begin{eqnarray}
20\log \frac {100}{\sqrt {1+\omega ^{2}}}=0 \\[ 5pt ]
\end{eqnarray}
\]
したがって,
\[
\begin{eqnarray}
\log \frac {100}{\sqrt {1+\omega ^{2}}}=0 \\[ 5pt ]
\end{eqnarray}
\]
\( \ \log=0 \ \)ということは,\( \ \log \ \)の中身が\( \ 1 \ \)ですから(\( \ 0 \ \)乗すると\( \ 1 \ \)),
\[
\begin{eqnarray}
\frac {100}{\sqrt {1+\omega ^{2}}}=1 \\[ 5pt ]
\end{eqnarray}
\]
つまり,\( \ \omega =200 \ \)を代入して,この等式が成立すれば,(3)が正答ということです。
(4),(5)についても同様ですから,このようになります。

では,(3)~(5)に\( \ \omega =200 \ \)を代入しましょう。

“む”と書いたのは,無視するという意味です。\( \ 2 \ \)桁以上小さい足し算・引き算は無視しています。
以上より,正答は(5)です。


