Contents
ゲインが\( \ g=20 \log_{10} W\left( \mathrm {j}\omega \right) \ \)となる理由―(キ)なぜ対数,なぜ\( \ 20 \ \)倍か―
ゲインが\( \ g=20 \log_{10} W\left( \mathrm {j}\omega \right) \ \)となる理由を,以下の\( \ 3 \ \)つに分けて解説します。
・対数を使う理由
・\( \ 10 \ \)倍する理由
・\( \ 2 \ \)倍する理由
\[
\begin{eqnarray}
\\[ 5pt ]
\end{eqnarray}
\]
・対数を使う理由
理由1:計算が容易だから
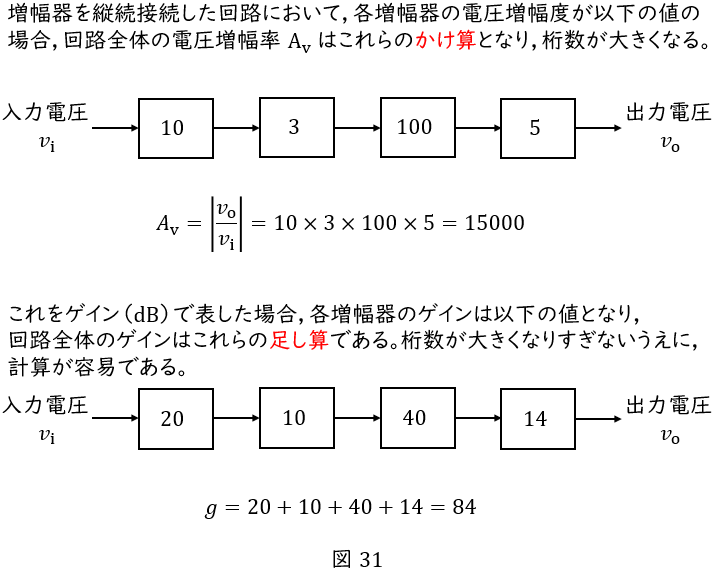
たくさんの増幅器を,縦列接続した回路をイメージしてください。回路全体の電圧増幅率を計算すると,かけ算の繰り返しが必要ですね。桁数が急激に増え,計算が大変です。
これをゲインで表した場合,ゲインは対数ですから,足し算で計算できます。桁数が急激に増えることはなく,計算が容易となります。
理由2:人間の感覚に合っている
“人間の感覚の大きさは,刺激の強さの対数に比例する”ことが知られており,これをウェーバー・フェヒナーの法則といいます。簡単に言うと,弱い刺激には敏感,強い刺激には鈍感ということです。
ウェーバー氏が見つけ,フェヒナー氏が発展させた法則なのですが,ウェーバー氏の重さの実験が分かりやすいです。
\( \ 100 \ \mathrm {g} \ \)の重りを手に乗せて,さらに\( \ 10 \ \mathrm {g} \ \)増やすと,被験者は“重くなった”と感じます。このときの重さの変化の感覚を覚えておきます。次は\( \ 1 000 \ \mathrm {g} \ \)の重りを乗せて,\( \ 10 \ \mathrm {g} \ \)増やすのですが,今度は変化を感じません。“重くなった”と感じるには,\( \ 100 \ \mathrm {g} \ \)程度が必要です。
音の大きさや明るさについても同様のことが確認されています。
つまり,“対数は人間の感覚の大きさを表すのに適している”ということなのです。
\[
\begin{eqnarray}
\\[ 5pt ]
\end{eqnarray}
\]
・\( \ 10 \ \)倍する理由
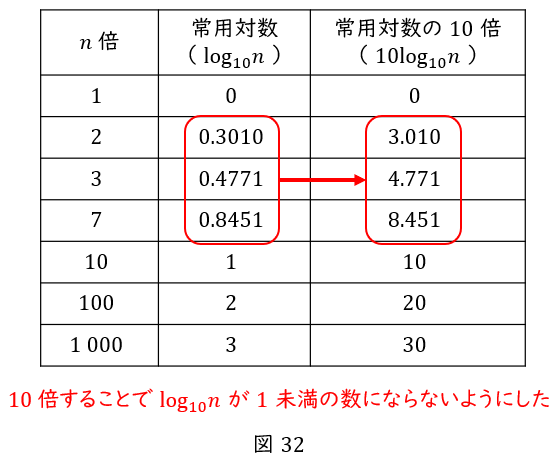
増幅器によって,出力電圧が入力電圧の\( \ n \ \)倍になる時,\( \ \log_{10} n \ \)は下表の数値になります。
\( \ 10 \ \)倍未満の場合,\( \ \log_{10} n \ \)は\( \ 1 \ \)未満となります。これでは増幅できていないのでは?と勘違いしかねません。
そこで,\( \ \log_{10} n \ \)を\( \ 10 \ \)倍することで,\( \ 10 \ \)倍未満でも\( \ 1 \ \)以上になるようにしたのです。
補足
ゲインの単位は\( \ \mathrm {dB} \ \)(デシベル)ですね。これは,\( \ \mathrm {B} \ \)(ベル)という単位に,\( \ \mathrm {d} \ \)(デシ)という接頭辞をつけたものです。
\( \ \mathrm {B} \ \)(ベル)とは,計測物理量と基準物理量の比の常用対数をとった単位です。
そして\( \ \mathrm {d} \ \)(デシ)とは,\( \ 10 \ \)分の\( \ 1 \ \)を意味する接頭辞です。
例えば,計測物理量が基準物理量の\( \ 2 \ \)倍になったとします。これの常用対数をとったものが\( \ \mathrm {B} \ \)(ベル)という単位なので,\( \ \log_{10} 2=0.3010 \ \)より,およそ\( \ 0.3 \ \mathrm {B} \ \)です。
これを\( \ \mathrm {dB} \ \)に直します。単位が\( \ 10 \ \)分の\( \ 1 \ \)になるので,数字は\( \ 10 \ \)倍の\( \ 3 \ \mathrm {dB} \ \)となります。
\( \ 1 \ \mathrm {m} \ \)を\( \ \mathrm {mm} \ \)に直すとき,単位が\( \ 1 \ 000 \ \)分の\( \ 1 \ \)になるので,数字は\( \ 1 \ 000 \ \)倍の\( \ 1 \ 000 \ \mathrm {mm} \ \)になりますよね。それと同じです。
\[
\begin{eqnarray}
\\[ 5pt ]
\end{eqnarray}
\]
・\( \ 2 \ \)倍する理由
もともとデシベルの定義が,電力の比だからです。
デシベルは,電力の比の常用対数の\( \ 10 \ \)倍と定義されます。
\[
\begin{eqnarray}
10\log_{10}\frac {P_{1}}{P_{2}} \\[ 5pt ]
\end{eqnarray}
\]
そして,\( \ 電力=電流\times 電圧 \ \)であり,オームの法則より,\( \ \displaystyle 電流=電圧 / 抵抗 \ \)ですから,\( \ 電力=電流\times 電圧=電圧^{2} / 抵抗 \ \)となり,電力は電圧の\( \ 2 \ \)乗に比例します。
\( \ \log \ \)の中身の\( \ 2 \ \)乗は,前に出すことができるので,
\[
\begin{eqnarray}
10\log_{10}\left( \frac {V_{1}}{V_{2}}\right) ^{2}&=& 10\times 2\log_{10} \frac {V_{1}}{V_{2}}=20\log_{10} \frac {V_{1}}{V_{2}} \\[ 5pt ]
\end{eqnarray}
\]
したがって,\( \ 20 \ \)倍となります。
以上より,ゲインの式は\( \ g=20 \log_{10} W\left( \mathrm {j}\omega \right) \ \)という,常用対数の\( \ 20 \ \)倍という形になるのです。



