サインカーブを理解する準備に,座標としてのサイン・コサインと弧度法について復習します。
練習問題をたくさん用意しているのですが,その目的は,弧度法の直感的なイメージを持つことです。
たとえば\( \ \displaystyle \frac{\pi}{6} \ \)と聞いて,どれくらいの角なのかが,頭の中にすぐ浮かぶことです。
練習問題をすべて解いた頃には,\( \ \displaystyle \frac{\pi}{6} \ \)がどんな大きさの角度か,そして\( \ \sin \displaystyle \frac{\pi}{6} \ \)がいくつがか,パッと答えられるようになるでしょう。
Contents
- 1 サイン・コサインは座標
- 2 弧度法の復習
- 3 例題\( \ 1 \ \) \( \ \sin \displaystyle \frac{\pi}{2} \ \),\( \ \cos \displaystyle \frac{\pi}{2} \ \)はいくつか
- 4 練習問題\( \ 1 \ \)
- 5 例題\( \ 2 \ \) \( \ \sin \left( -\displaystyle \frac{\pi}{2}\right) \ \),\( \ \cos \left(-\displaystyle \frac{\pi}{2}\right) \ \)はいくつか
- 6 練習問題\( \ 2 \ \)
- 7 特別な直角三角形の復習
- 8 例題\( \ 3\ \) \( \ \sin \displaystyle \frac{3}{4}\pi \ \),\( \ \cos \displaystyle \frac{3}{4}\pi \ \)はいくつか
- 9 練習問題\( \ 3\ \)
サイン・コサインは座標
サイン・コサインはもともと,「三角形の,辺の長さと辺の長さの比」です。
しかし,三角形で考えている限り,角度は\( \ 0 \ \)以上\( \ \displaystyle \frac{\pi}{2} \ \)未満に限定されます。
そこで,ここからは三角形のことは忘れて,サイン・コサインのことを,「座標」だと考え直します。言い換えると,サインとは単位円の\( \ y \ \)座標のこと,コサインとは\( \ x \ \)座標のことだと考えるのです。
単位円とは何かは,三角比⑥を参照ください。
弧度法の復習
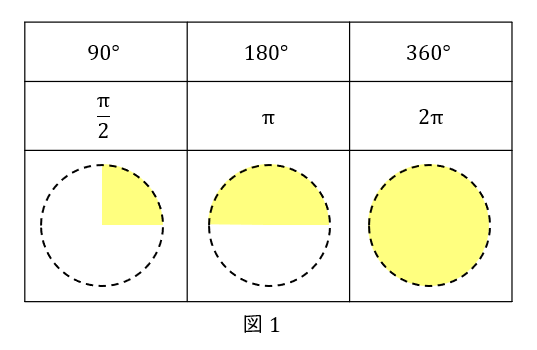
ここで弧度法を復習しましょう。\( \ \displaystyle \frac{\pi}{2} \ \)は\( \ 90^\circ \ \),\( \ \pi \ \)は\( \ 180^\circ \ \),\( \ 2 \pi \ \)は\( \ 360^\circ \ \)です(三角比⑤より)。
言い換えれば,
\( \ \displaystyle \frac{\pi}{2} \ \)は\( \ \displaystyle \frac{1}{4} \ \)円,\( \ \pi \ \)は半円,\( \ 2 \pi \ \)は円です。
\( \ \displaystyle \frac{\pi}{2} \ \)と聞いたら,すぐさま\( \ \displaystyle \frac{1}{4} \ \)円をイメージできるようにしましょう。
例題\( \ 1 \ \) \( \ \sin \displaystyle \frac{\pi}{2} \ \),\( \ \cos \displaystyle \frac{\pi}{2} \ \)はいくつか
\( \ \displaystyle \frac{\pi}{2} \ \)は,\( \ \displaystyle \frac{1}{4} \ \)円が\( \ 1 \ \)つです。
単位円の点\( \ \mathrm {P} \ \)ですから,座標は\( \ ( 0,1 ) \ \)です。
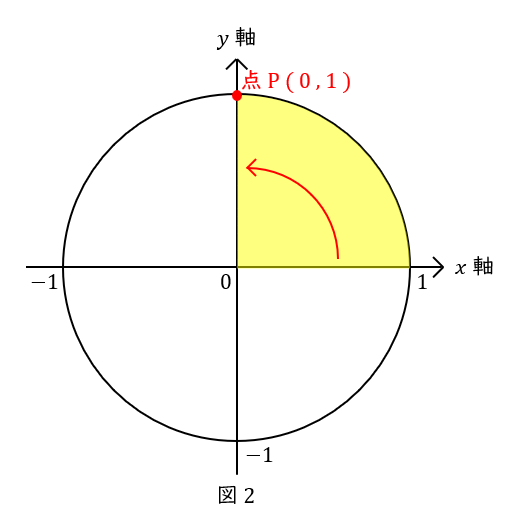
サインは\( \ y \ \)座標,コサインは\( \ x \ \)座標ですから,\( \ \sin \displaystyle \frac{\pi}{2} =1 \ \),\( \ \cos \displaystyle \frac{\pi}{2} =0 \ \)です。
サイン・コサインを座標だと定義し直したおかげで,このように三角形が描けない場合でも,サイン・コサインが存在できるのです。
練習問題\( \ 1 \ \)
\( \ \theta \ \)が次の角度のとき,\( \ \sin \theta \ \),\( \ \cos \theta \ \)はいくつか
\( \ (1-1) \ \) \( \ \theta = \pi \ \)
\( \ (1-2) \ \) \( \ \theta = \displaystyle \frac{3}{2}\pi \ \)
\( \ (1-3) \ \) \( \ \theta = 2\pi \ \)
\( \ (1-4) \ \) \( \ \theta = 0 \ \)
\( \ (1-5) \ \) \( \ \theta = 3\pi \ \)
\( \ (1-6) \ \) \( \ \theta = \displaystyle \frac{203}{2}\pi \ \)
\( \ \displaystyle \frac{\pi}{2} \ \)は\( \ \displaystyle \frac{1}{4} \ \)円,\( \ \pi \ \)は半円,\( \ 2 \pi \ \)は円,でしたね。
そしてサインは\( \ y \ \)座標,コサインは\( \ x \ \)座標です。
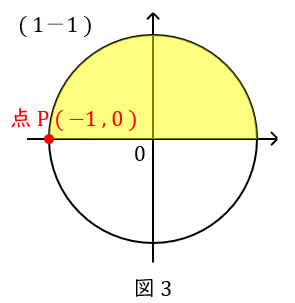
\( \ (1-1) \ \) \( \ \sin \pi =0 \ \),\( \ \cos \pi =-1 \ \)
\( \ \pi \ \)は半円ですから,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( -1,0 ) \ \)です。
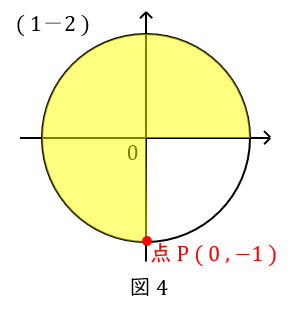
\( \ (1-2) \ \) \( \ \sin \displaystyle \frac{3}{2}\pi =-1 \ \),\( \ \cos \displaystyle \frac{3}{2}\pi =0 \ \)
\( \ \displaystyle \frac{3}{2}\pi \ \)は,\( \ \displaystyle \frac{1}{4} \ \)円が\( \ 3 \ \)つですから,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( 0,-1 ) \ \)です。
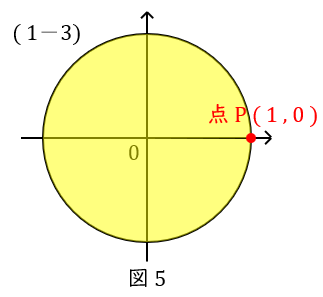
\( \ (1-3) \ \) \( \ \sin 2\pi =0 \ \),\( \ \cos 2\pi =1 \ \)
\( \ 2 \pi \ \)は円ですから,スタート地点に戻ります。
座標は\( \ (1,0 ) \ \)です。
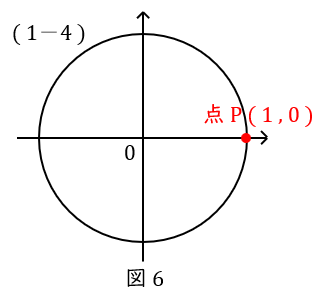
\( \ (1-4) \ \) \( \ \sin 0 =0 \ \),\( \ \cos 0 =1 \ \)
スタート地点である点\( \ \mathrm {P} \ \)です。座標は\( \ ( 1,0 ) \ \)です。
当然ながら,\( \ \theta = 2\pi \ \)と同じ答えになります。
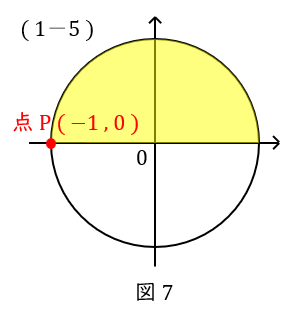
\( \ (1-5) \ \) \( \ \sin 3 \pi =0 \ \),\( \ \cos 3 \pi =-1 \ \)
\( \ 3\pi \ \)は,\( \ 2\pi+\pi \ \)ですから,一周とさらに半周回って,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( -1,0 ) \ \)です。
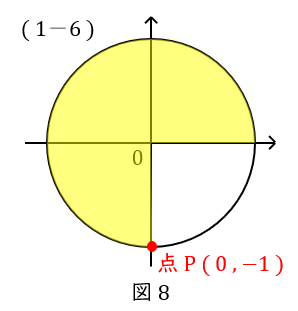
\( \ (1-6) \ \) \( \ \sin \displaystyle \frac{203}{2}\pi =0 \ \),\( \ \cos \displaystyle \frac{203}{2}\pi =-1 \ \)
急に大きな数字になって驚いたかもしれませんが,\( \ (1-5) \ \)と同じ考え方で解けます。
\( \ \displaystyle \frac{203}{2}\pi=100\pi+\displaystyle \frac{3}{2}\pi\ \) です。
\( \ 100\pi \ \)とは\( \ 2\pi\times 50 \ \)ですから,\( \ 50 \ \)周回るということです。
これにプラス\( \ \displaystyle \frac{3}{2}\pi \ \)ですから,\( \ \displaystyle \frac{1}{4} \ \)円が\( \ 3 \ \)つで,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( 0,-1 ) \ \)です。
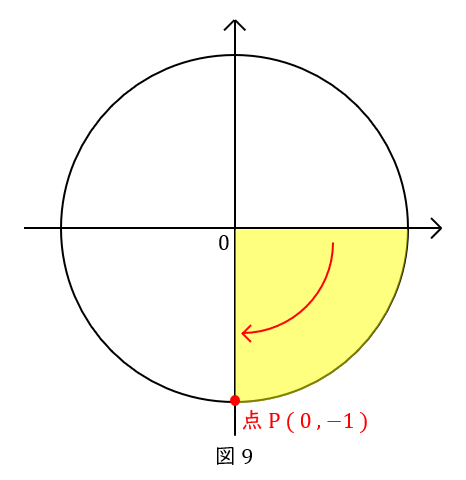
例題\( \ 2 \ \) \( \ \sin \left( -\displaystyle \frac{\pi}{2}\right) \ \),\( \ \cos \left(-\displaystyle \frac{\pi}{2}\right) \ \)はいくつか
\( \ \theta \ \)はマイナスでも構いません。プラスがスタート地点から上方向(反時計回り)ですから,マイナスは下方向(時計回り)に回ります。\( \ \displaystyle \frac{\pi}{2} \ \)とは\( \ \displaystyle \frac{1}{4} \ \)円ですから単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( 0,-1 ) \ \)ですから,\( \ \sin \left(-\displaystyle \frac{\pi}{2}\right) =-1 \ \),\( \ \cos \left(-\displaystyle \frac{\pi}{2}\right) =0 \ \)です。
練習問題\( \ 2 \ \)
\( \ \theta \ \)が次の角度のとき,\( \ \sin \theta \ \),\( \ \cos \theta \ \)を答えよ。
\( \ (2-1) \ \) \( \ \theta = -\pi \ \)
\( \ (2-2) \ \) \( \ \theta = -\displaystyle \frac{3}{2}\pi \ \)
\( \ (2-3) \ \) \( \ \theta = -2\pi \ \)
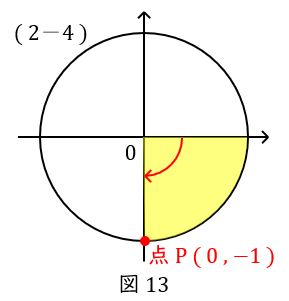
\( \ (2-4) \ \) \( \ \theta = -\displaystyle \frac{101}{2}\pi \ \)
マイナスですからスタート地点から下方向(時計回り)に回るところに注意しましょう。
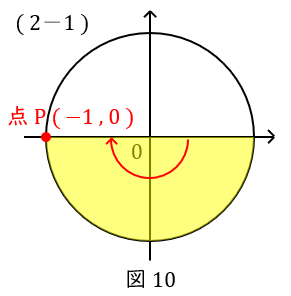
\( \ (2-1) \ \) \( \ \sin (-\pi) =0 \ \),\( \ \cos (-\pi) =-1 \ \)
\( \ \pi \ \) は半円ですから,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( -1,0 ) \ \)です。
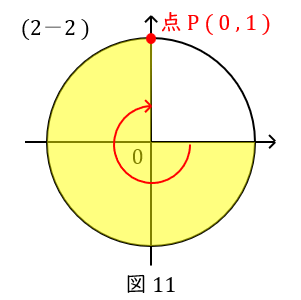
\( \ (2-2) \ \) \( \ \sin \left(-\displaystyle \frac{3}{2}\pi\right) =1 \ \),\( \ \cos \left(-\displaystyle \frac{3}{2}\pi\right) =0 \ \)
\( \ \displaystyle \frac{3}{2}\pi \ \)は,\( \ \displaystyle \frac{1}{4} \ \)円が\( \ 3 \ \)つですから,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( 0,1 ) \ \)です。
\( \ (2-3) \ \) \( \ \sin (-2\pi) =0 \ \),\( \ \cos (-2\pi) =1 \ \)
\( \ 2 \pi \ \)は円ですから,スタート地点に戻ります。
座標は\( \ ( 1,0 ) \ \)です。
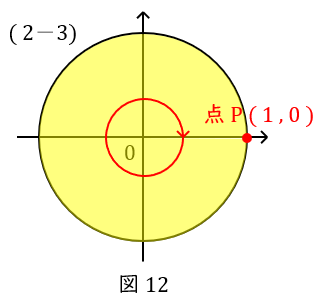
\( \ (2-4) \ \) \( \ \sin \left(-\displaystyle \frac{101}{2}\pi\right) =-1 \ \),\( \ \cos \left(-\displaystyle \frac{101}{2}\pi\right) =0 \ \)
\( \ -\displaystyle \frac{101}{2}\pi=-50\pi-\displaystyle \frac{\pi}{2} \ \) です。
\( \ -50 \pi \ \)とは\( \ -2 \pi \times 25 \ \)ですから,スタート地点から下の方向に\( \ 25 \ \)周回るということです。
これに\( \ -\displaystyle \frac{\pi}{2} \ \)ですから,スタート地点から下の方向に\( \ \displaystyle \frac{1}{4} \ \)周回って,単位円の点\( \ \mathrm {P} \ \)です。
座標は\( \ ( 0,-1 ) \ \)です。
特別な直角三角形の復習
まずは弧度法の復習です。
\( \ \displaystyle \frac{\pi}{4} \ \)は\( \ 45^\circ \ \),\( \ \displaystyle \frac{\pi}{6} \ \)は\( \ 30^\circ \ \),\( \ \displaystyle \frac{\pi}{3} \ \)は\( \ 60^\circ \ \)です。
いずれも分母とのかけ算で\( \ 180 \ \)になるのでしたね。
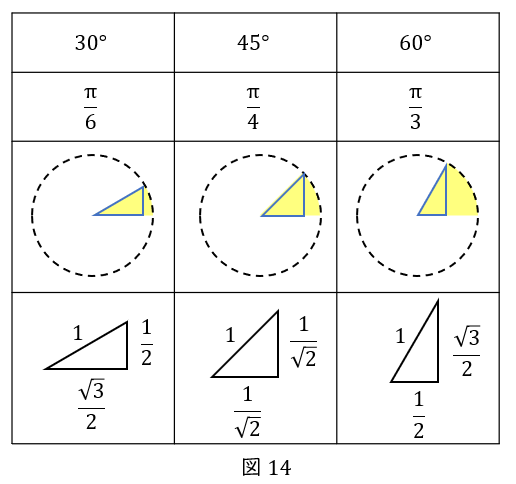
「\( \ \pi \ \)分の何」と聞いたら,どれくらいの扇形なのかをすぐにイメージできるようになりましょう。
次に辺の長さの比の復習です。
\( \ \displaystyle \frac{\pi}{4} \ \)と\( \ \displaystyle \frac{\pi}{4} \ \)の直角二等辺三角形は,\( \ 1:1:\sqrt{2} \ \)です。
斜辺を\( \ 1\ \)にすると,\( \ \displaystyle \frac{1}{\sqrt{2}} : \displaystyle \frac{1}{\sqrt{2}} : 1\ \)です。
\( \ \displaystyle \frac{\pi}{6} \ \)と\( \ \displaystyle \frac{\pi}{3} \ \)の直角三角形は,\( \ 1:2:\sqrt{3} \ \)です。
斜辺を\( \ 1\ \)にすると,\( \ \displaystyle \frac{1}{2} : 1 : \displaystyle \frac{\sqrt{3}}{2}\ \)です。
三角比④で紹介しました。
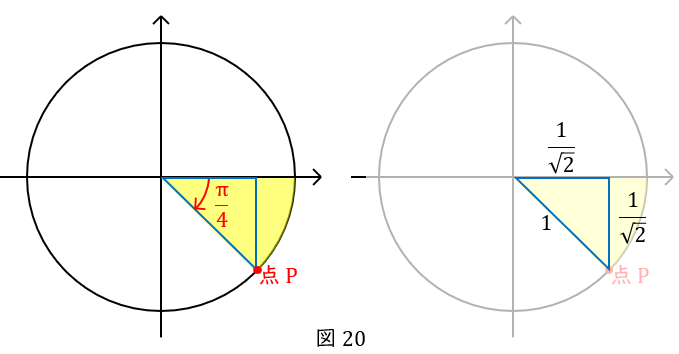
例題\( \ 3\ \) \( \ \sin \displaystyle \frac{3}{4}\pi \ \),\( \ \cos \displaystyle \frac{3}{4}\pi \ \)はいくつか
\( \ \displaystyle \frac{\pi}{4} \ \)が\( \ 3\ \)つですから,単位円の点\( \ \mathrm {P} \ \)です。
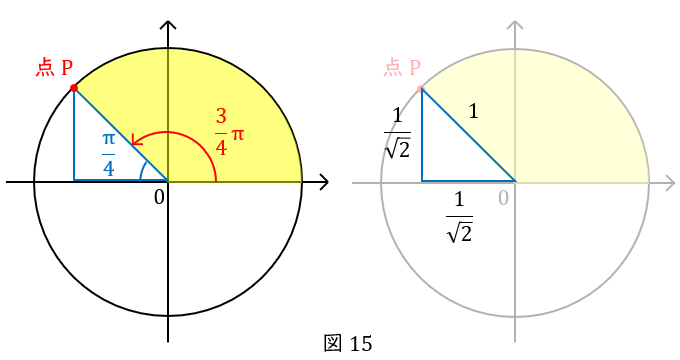
この点の座標を知るために,\( \ x \ \)軸に線をおろして,直角を作りましょう。
図の水色の角度は,直線(\( \ \pi \ \))から\( \ \displaystyle \frac{3}{4}\pi \ \)を引いて\( \ \displaystyle \frac{\pi}{4} \ \)です。
半径\( \ 1\ \)の円ですから斜辺の長さは\( \ 1 \ \)です。
\( \ \displaystyle \frac{\pi}{4} \ \)の直角三角形では,辺の長さの比は\( \ \displaystyle \frac{1}{\sqrt{2}} : \displaystyle \frac{1}{\sqrt{2}} : 1\ \)となるので,底辺と高さは\( \ \displaystyle \frac{1}{\sqrt{2}} \ \)です。
したがって,座標は\( \ \left(-\displaystyle \frac{1}{\sqrt{2}} , \displaystyle \frac{1}{\sqrt{2}}\right) \ \)です。
以上より,\( \ \sin \displaystyle \frac{3}{4}\pi =\displaystyle \frac{1}{\sqrt{2}} \ \),\( \ \cos \displaystyle \frac{3}{4}\pi = -\displaystyle \frac{1}{\sqrt{2}} \ \)
※\( \ y \ \)軸に線をおろしても同様に解くことができます。
練習問題\( \ 3\ \)
\( \ \theta \ \)が次の角度のとき,\( \ \sin \theta \ \),\( \ \cos \theta \ \)を答えよ。
\( \ (3-1) \ \) \( \ \theta = \displaystyle \frac{2}{3}\pi \ \)
\( \ (3-2) \ \) \( \ \theta = \displaystyle \frac{5}{6}\pi \ \)
\( \ (3-3) \ \) \( \ \theta = -\displaystyle \frac{\pi}{3} \ \)
\( \ (3-4) \ \) \( \ \theta = -\displaystyle \frac{5}{6}\pi \ \)
\( \ (3-5) \ \) \( \ \theta = -\displaystyle \frac{\pi}{4} \ \)
\( \ x \ \)軸に線をおろして直角三角形を作って考えましょう。マイナスの場合はスタート地点から下方向に回る(時計回り)ことに注意しましょう。
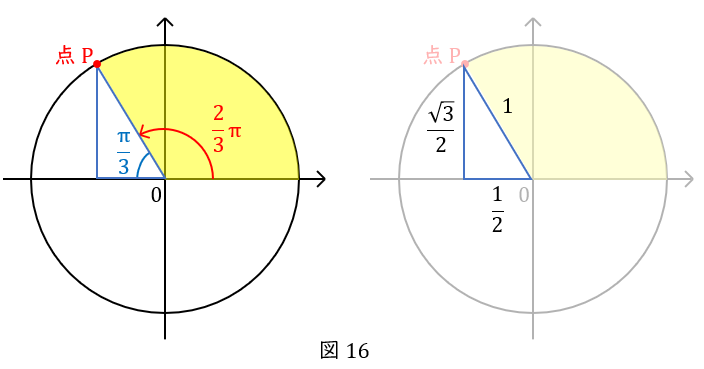
\( \ (3-1) \ \) \( \ \sin \displaystyle \frac{2}{3}\pi = \displaystyle \frac{\sqrt{3}}{2} \ \),\( \ \cos \displaystyle \frac{2}{3}\pi =- \displaystyle \frac{1}{2} \ \)
\( \ \displaystyle \frac{\pi}{3} \ \)が\( \ 2 \ \)つですから,単位円の点\( \ \mathrm {P} \ \)です。
この点の座標を知るには,\( \ x \ \)軸に線をおろして,直角三角形を作りましょう。
図の水色の角度は,直線(\( \ \pi \ \))から\( \ \displaystyle \frac{2}{3}\pi \ \)を引いて\( \ \displaystyle \frac{\pi }{3}\ \)です。
よって,図のようになるので,座標は\( \ \left(-\displaystyle \frac{1}{2} , \displaystyle \frac{\sqrt{3}}{2}\right) \ \)です。
\( \ (3-2) \ \) \( \ \sin \displaystyle \frac{5}{6}\pi =\displaystyle \frac{1}{2} \ \),\( \ \cos \displaystyle \frac{5}{6}\pi = -\displaystyle \frac{\sqrt{3}}{2} \ \)
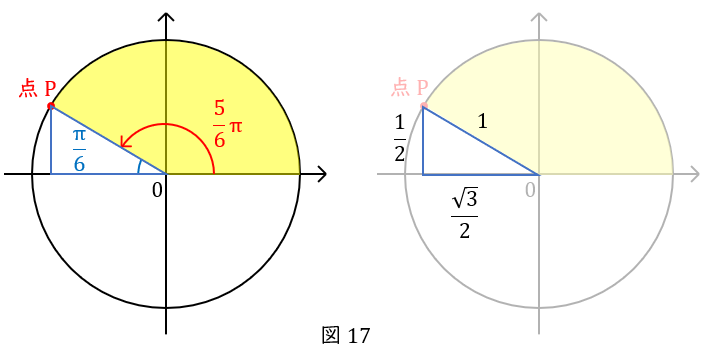
\( \ \displaystyle \frac{5}{6}\pi \ \)を,\( \ \displaystyle \frac{\pi}{6} \ \)が\( \ 5 \ \)つ,と考えてもイメージできないと思います。
そこで,\( \ \displaystyle \frac{5}{6}\pi \ \)を,”直線(\( \ \pi \ \))に,\( \ \displaystyle \frac{\pi}{6} \ \)足りない”と考えます。単位円の点\( \ \mathrm {P} \ \)です。
この点の座標を知るには,\( \ \mathrm {x} \ \)軸に線をおろして,直角三角形を作りましょう。
図のようになるので,座標は\( \ \left(-\displaystyle \frac{\sqrt{3}}{2} , \displaystyle \frac{1}{2}\right) \ \)です。
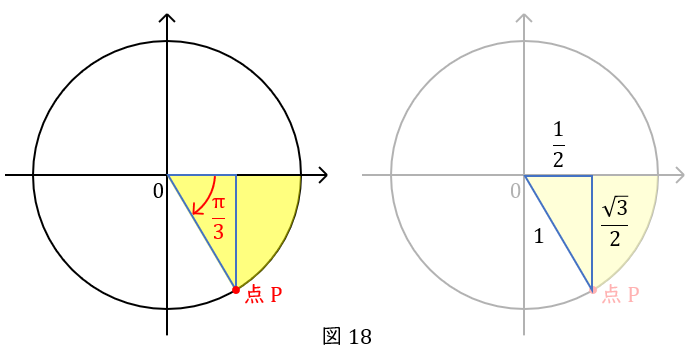
\( \ (3-3) \ \) \( \ \sin \left(-\displaystyle \frac{\pi}{3}\right) = -\displaystyle \frac{\sqrt{3}}{2} \ \),\( \ \cos \left(-\displaystyle \frac{\pi}{3}\right) = \displaystyle \frac{1}{2} \ \)
スタート地点から下の方向に\( \ \displaystyle \frac{\pi}{3} \ \)だけ回るので,単位円の点\( \ \mathrm {P} \ \)です。
この点の座標を知るには,\( \ x \ \)軸に線をおろして,直角三角形を作りましょう。
図のようになるので,座標は\( \ \left(\displaystyle \frac{1}{2} , -\displaystyle \frac{\sqrt{3}}{2}\right) \ \)です。
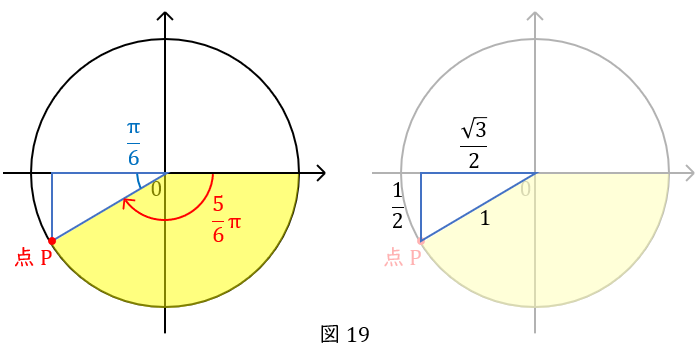
\( \ (3-4) \ \) \( \ \sin \left(-\displaystyle \frac{5}{6}\pi\right) =-\displaystyle \frac{1}{2} \ \),\( \ \cos \left(-\displaystyle \frac{5}{6}\pi\right) =-\displaystyle \frac{\sqrt{3}}{2} \ \)
スタート地点から下の方向に\( \ \displaystyle \frac{5}{6}\pi \ \)だけ回ります。
\( \ (3-2) \ \)と同様に,\( \ \displaystyle \frac{5}{6}\pi \ \)を,”直線(\( \ \pi \ \))に,\( \ \displaystyle \frac{\pi}{6} \ \)足りない”と考えます。
単位円の点\( \ \mathrm {P} \ \)です。
この点の座標を知るには,\( \ x \ \)軸に線をおろして,直角三角形を作りましょう。
図のようになるので,座標は\( \ \left(-\displaystyle \frac{\sqrt{3}}{2} , -\displaystyle \frac{1}{2}\right) \ \)です。
\( \ (3-5) \ \) \( \ \sin \left(- \displaystyle \frac{\pi}{4}\right) =-\displaystyle \frac{1}{\sqrt{2}} \ \),\( \ \cos \left(-\displaystyle \frac{\pi}{4}\right) =\displaystyle \frac{1}{\sqrt{2}} \ \)
スタート地点から下の方向に\( \ \displaystyle \frac{\pi}{4} \ \)だけ回るので,単位円の点\( \ \mathrm {P} \ \)です。
この点の座標を知るには,\( \ x \ \)軸に線をおろして,直角三角形を作りましょう。
図のようになるので,座標は\( \ \left(\displaystyle \frac{1}{\sqrt{2}} , -\displaystyle \frac{1}{\sqrt{2}}\right) \ \)です。