【三角関数③】”サイン”カーブの名前の由来。サインを使ってサインカーブが描けることをくわしく解説

三角関数①では，サインカーブをばねの動きで解説しました。
しかし，これではなぜ”サイン”カーブなのかが分かりません。
サインカーブとは，サインの値を使って描くことができる曲線です。

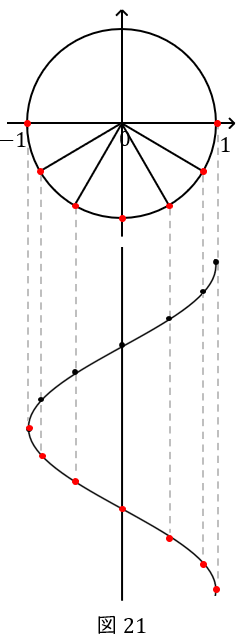
円運動の\( \ y \ \)軸方向の動きだけに注目する

点\( \ \mathrm {P} \ \)が円周上を一定の速度で動くとします。分かりやすいように，\( \ 3 \ \)秒間で\( \ \displaystyle \frac{\pi}{2} \ \)だけ動くとしましょう。

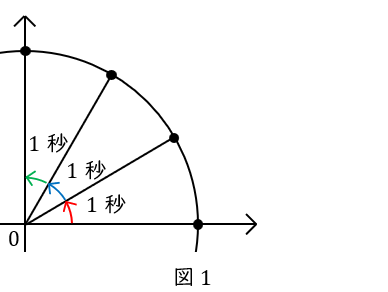
\( \ 1 \ \)秒間に\( \ \displaystyle \frac{\pi}{6} \ \)動くということです。

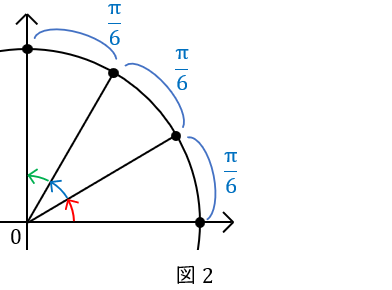
ここで，点\( \ \mathrm {P} \ \)が動いた距離そのものではなく，”\( \ y \ \)軸方向にどれだけ動いたか”だけに注目します。

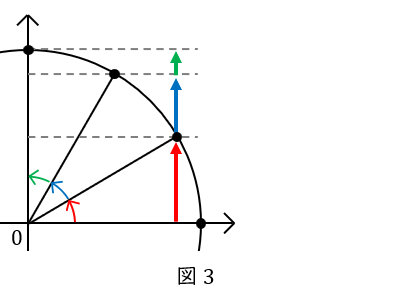
最初の\( \ 1 \ \)秒（赤色）が長く，次の\( \ 1 \ \)秒（水色）が中くらい，最後の\( \ 1 \ \)秒（緑色）が短くなります。三角関数①で解説した，サインカーブの特徴ですね。

次に，時間を横軸にとって，点\( \ \mathrm {P} \ \)の\( \ y \ \)座標を縦軸にしたグラフをかきます。
こうすることで，円周上を回る点\( \ \mathrm {P} \ \)を，時系列で書き表すことができます。

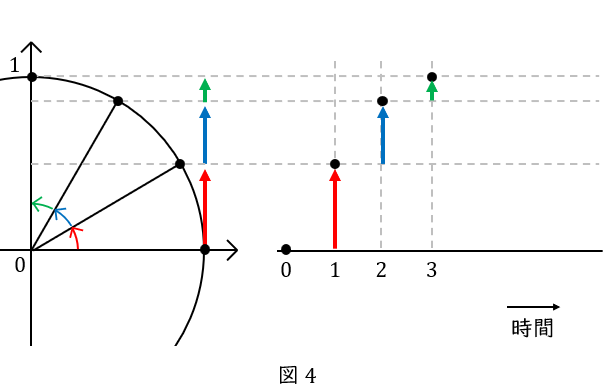
点\( \ \mathrm {P} \ \)をもっと動かしましょう。最大値である\( \ 1 \ \)から\( \ 0 \ \)に向かうときは，最初の\( \ 1 \ \)秒（緑色）が短く，次の\( \ 1 \ \)秒（水色）が中くらい，最後の\( \ 1 \ \)秒（赤色）が長くなります。だんだんとサインカーブが見えてきましたね。

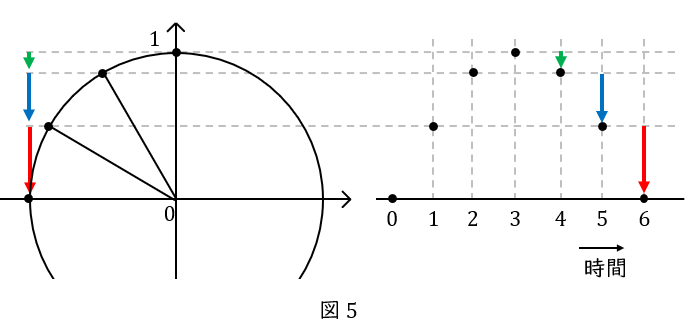
今度は円の左下です。まずは\( \ 0 \ \)から\( \ -1 \ \)に向かいます。ここでも，最初の\( \ 1 \ \)秒（赤色）が長く，次の\( \ 1 \ \)秒（水色）が中くらい，最後の\( \ 1 \ \)秒（緑色）が短くなります。

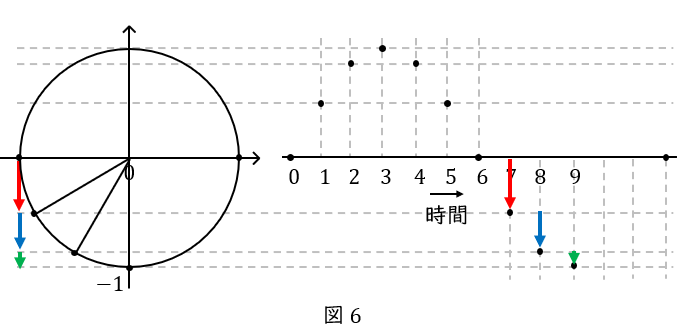
最後は円の右下です。最小値である\( \ -1 \ \)から\( \ 0 \ \)へ向かいます。最初の\( \ 1 \ \)秒（緑色）が短く，次の\( \ 1 \ \)秒（水色）が中くらい，最後の\( \ 1 \ \)秒（赤色）が長くなります。

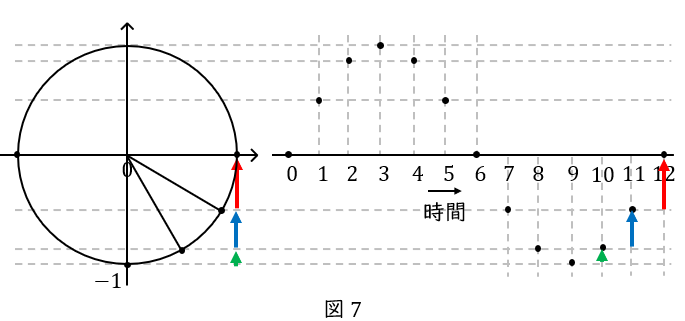
以上，点\( \ \mathrm {P} \ \)の”\( \ y \ \)軸方向の動き”に注目しました。言い換えれば，\( \ y \ \)座標の時間変化を描いたということです。
そして，単位円の\( \ y \ \)座標とはサインのことですから，この曲線を”サイン”カーブといいます。

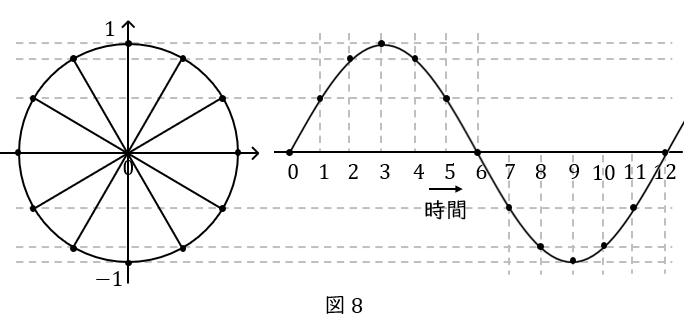
変化量はどれくらい違うのか

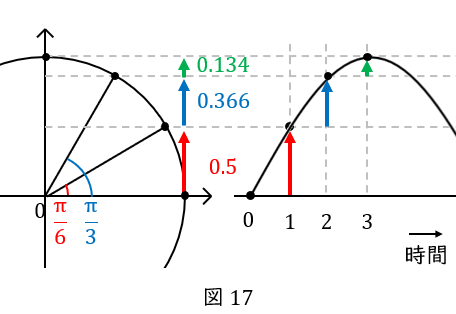
前の説明では，”長い，中くらい，短い…“と抽象的に表現しましたが，実際にどれくらい違うのかを見てきましょう。

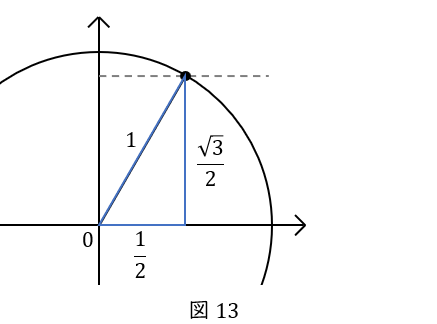
点\( \ \mathrm {P} \ \)は\( \ 1 \ \)秒間で\( \ \displaystyle \frac{\pi}{6} \ \)動きます。点\( \ \mathrm {P} \ \)から\( \ x \ \)軸に線をおろして直角三角形を作ると，下図のようになります。

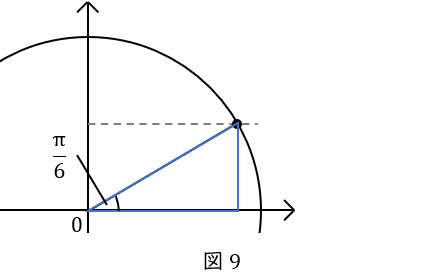
\( \ \displaystyle \frac{\pi}{6} \ \)の角度を持つ直角三角形は特別で，辺の比が\( \ 1:\displaystyle \frac{1}{2}:\displaystyle \frac{\sqrt{3}}{2} \ \)でしたね。そして，単位円の半径が\( \ 1 \ \)なので，三角形の斜辺の長さは\( \ 1 \ \)です。よって，底辺が\( \ \displaystyle \frac{\sqrt{3}}{2} \ \)，高さが\( \ \displaystyle \frac{1}{2} \ \)となります。

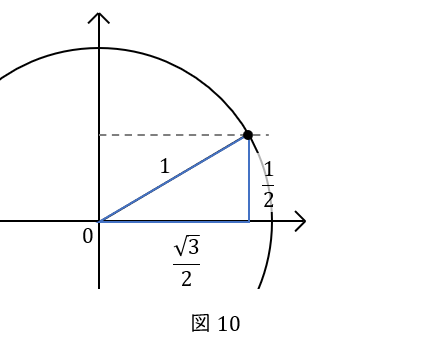
以上より点\( \ \mathrm {P} \ \)が\( \ y \ \)軸方向に動いた距離は\( \ \displaystyle \frac{1}{2} \ \)です。

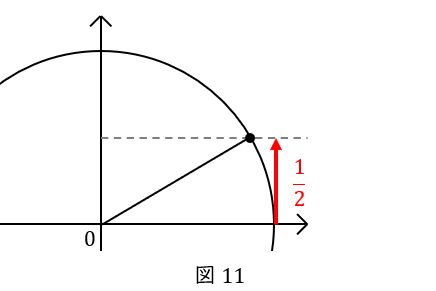
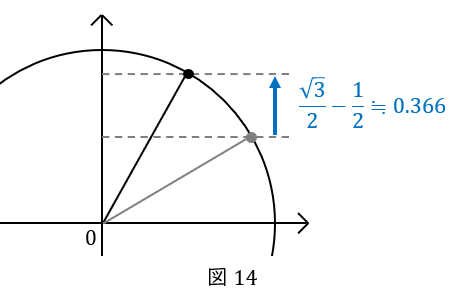
次の\( \ 1 \ \)秒間で点\( \ \mathrm {P} \ \)はさらに\( \ \displaystyle \frac{\pi}{6} \ \)進みますから，\( \ x \ \)軸と作る角度は\( \ \displaystyle \frac{\pi}{3} \ \)となります。

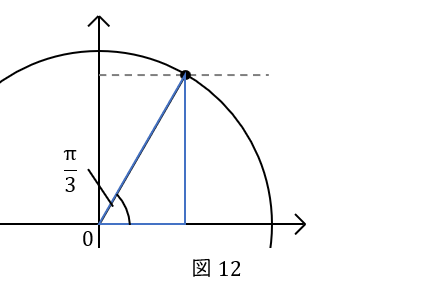
\( \ \displaystyle \frac{\pi}{3} \ \)の角を持つ直角三角形は特別な三角形で， 辺の比が\( \ 1:\displaystyle \frac{1}{2}:\displaystyle \frac{\sqrt{3}}{2} \ \)でしたね。
そして，単位円の半径が\( \ 1 \ \)なので，三角形の斜辺の長さは\( \ 1 \ \)です。
よって，底辺が\( \ \displaystyle \frac{1}{2} \ \)，高さが\( \ \displaystyle \frac{\sqrt{3}}{2} \ \)となります。

以上より，この\( \ 1 \ \)秒間で点\( \ \mathrm {P} \ \)が\( \ y \ \)軸方向に動いた距離は\( \ \displaystyle \frac{\sqrt{3}}{2} – \displaystyle \frac{1}{2}\ \)です。

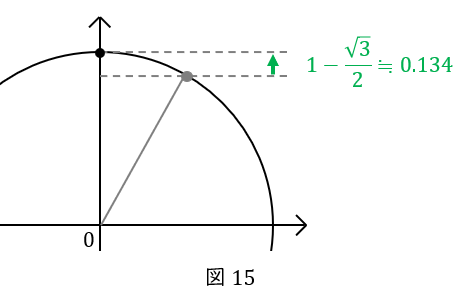
そして，次の\( \ 1 \ \)秒間で点\( \ \mathrm {P} \ \)は\( \ (0,1) \ \)に移動します。この\( \ 1 \ \)秒間で点\( \ \mathrm {P} \ \)が\( \ y \ \)軸方向に動いた距離は\( \ 1-\displaystyle \frac{\sqrt{3}}{2} \ \)です。

以上をまとめるとこちらです。点\( \ \mathrm {P} \ \)の\( \ y \ \)軸方向の動きは，\( \ 3 \ \)秒間で\( \ 0 \ \)から\( \ 1 \ \)まで進むわけですが，最初の\( \ 1 \ \)秒間で\( \ 0.5 \ \)進み，最後の\( \ 1 \ \)秒間は\( \ 0.134 \ \)しか進まないことが分かります。

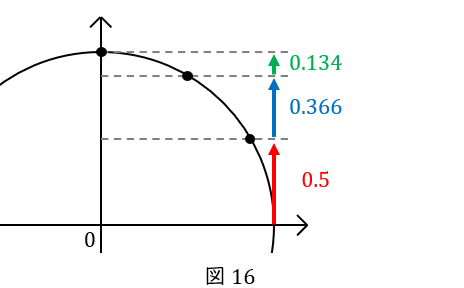
時間を横軸にとって，サインカーブにしたものがこちらです。\( \ 0 \ \)から最大値である\( \ 1 \ \)に向かうにつれて，増加量が小さくなることが分かります。

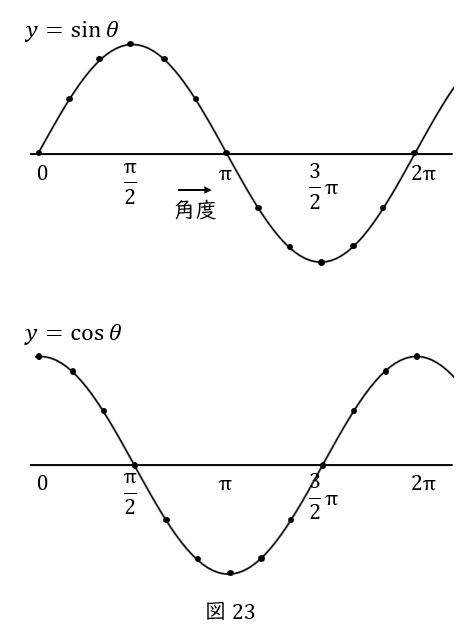
そして，ここまでは時間を横軸にとっていましたが，一定の速度で動いているわけですから，角度を横軸に取っても同じです。円の一周が\( \ 2 \pi \ \)ですから，波の周期も\( \ 2 \pi \ \)となります。

交流電源の電圧はサインカーブで変化する

ここまでの解説で，サインカーブがその名の通り”サイン”のカーブであることが分かりました。

ここで，目的を見失ってはいけないので，そもそもなぜサインカーブを勉強しているかを復習します。

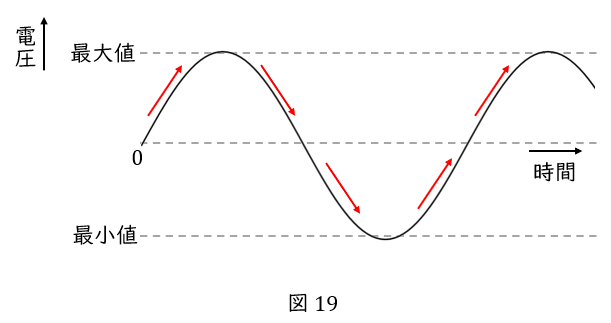
交流電源の電圧がサインカーブで変化するからです（三角関数①）。
交流電源の電圧は，ある時点で\( \ 0 \ \)であり，徐々に上がって最大値となり，徐々に下がって再び\( \ 0 \ \)になり，今度はマイナスの方向に向かい，最小値をとって，また\( \ 0 \ \)に戻り，再びプラス方向に上がって最大値を迎え…と繰り返します。
そして電圧の上がり方・下がり方は一定ではないため，ギザギザ線ではなく，ゆるやかなサインカーブとなります。

コサインカーブはどうなるか

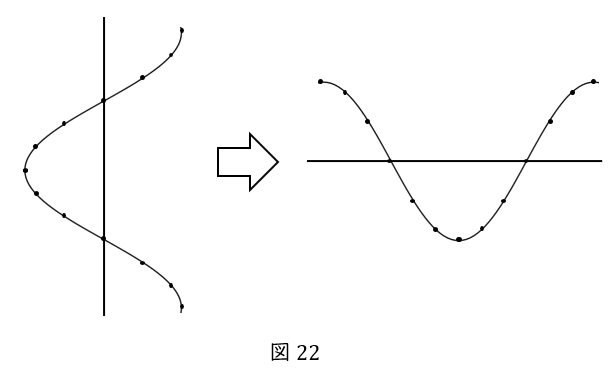
コサインカーブもサインカーブと同様に描くことができます。コサインとは\( \ x \ \)座標のことですから，単位円の下側にカーブを描く方が分かりやすいでしょう。

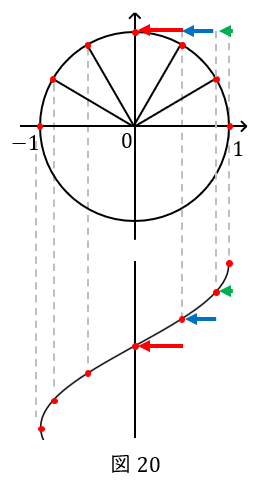
スタートの座標は\( \ ( 1,0 ) \ \)で，コサインとは\( \ x \ \)座標のことですから，コサインカーブは最大値である\( \ 1 \ \)から始まります。
その後の\( \ x \ \)座標の動きを，時間または角度ごとに描いたのがコサインカーブです。

サインカーブと同様に，点\( \ \mathrm {P} \ \)が\( \ 1 \ \)秒で\( \ \displaystyle \frac{\pi}{6} \ \)だけ移動するとします（なお，単位円は半径\( \ 1 \ \)の円なので，\( \ \displaystyle \frac{\pi}{6} \ \)というのは，角度のことでもあり，円周の長さでもあります）。

点\( \ \mathrm {P} \ \)の移動距離のうち，\( \ x \ \)軸方向の動きだけに注目すると，最初の\( \ 1 \ \)秒は緑色矢印，次の\( \ 1 \ \)秒は水色矢印，次の\( \ 1 \ \)秒は赤矢印です。

サインカーブと同様に，最大値である\( \ 1 \ \)から\( \ 0 \ \)に向かうにつれて減少量が大きくなっています。

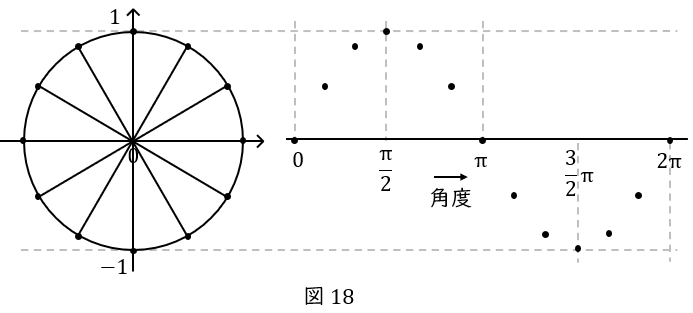
その後，点\( \ \mathrm {P} \ \)が\( \ \displaystyle \frac{\pi}{2} \ \)まで移動したら座標\( \ (0,1) \ \)ですからコサインは\( \ 0 \ \)，

\( \ \pi \ \)なら座標は\( \ ( -1,0 ) \ \)ですからコサインは\( \ -1 \ \)，

\( \ \displaystyle \frac{3}{2}\pi \ \)なら座標は\( \ ( 0,1 ) \ \)ですからコサインは\( \ 0 \ \)，

\( \ 2 \pi \ \)なら座標は\( \ ( 1,0 ) \ \)ですからコサインは\( \ 1 \ \)となります。

向きを直すとこちらです。

なお，\( \ \theta \ \)が\( \ 2 \pi \ \)よりずっと大きい値や負の値であっても，コサインの値は存在しますから， \( \ 2 \pi \ \)を一つの周期としてずっと続くカーブとなります。これもサインカーブと同じですね。
サインカーブとコサインカーブを並べて比較すると図\( \ 23 \ \)です。コサインカーブは，サインカーブを\( \ \displaystyle \frac{\pi}{2} \ \)だけ左にずらしたような形となります。

練習問題

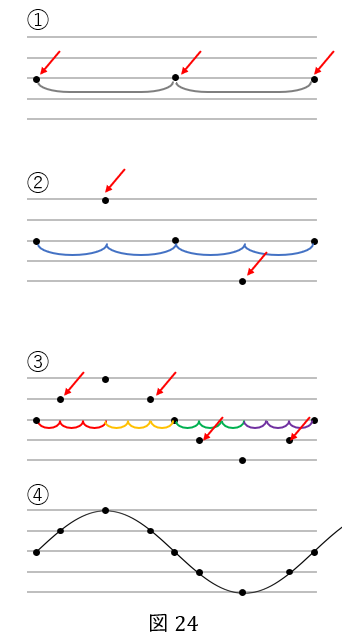
ちょっと変わった練習問題となりますが，フリーハンドでサインカーブを描いてみましょう。
電験の問題を解くために，正確なサインカーブを描く必要はありません。しかし，あまりにも雑な図を描いてしまうと，自分の書いた図に惑わされて，問題が解きづらくなることも。
そこで，時間のロスにならない程度に，”いい感じの”サインカーブを描くコツを紹介します。