【三角関数④】周期・周波数・回転数・角速度（角周波数・角振動数）の定義と関係をくわしく解説

周期・周波数・回転数・角速度を学習します。これらの定義と関係式は非常に重要なので，しっかり理解しておきましょう。

周期

サインカーブはこれまで述べた通り，円周上を一定の速度で動く点\( \ \mathrm {P} \ \)の，\( \ y \ \)軸方向の動きだけを取り出したものです。ですから，角度\( \ \theta \ \)を横軸とすると，\( \ 2 \pi \ \)が\( \ 1 \ \)サイクルとなります。

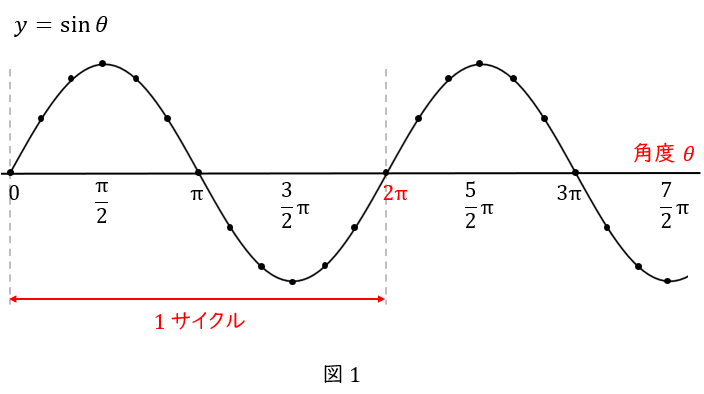
点\( \ \mathrm {P} \ \)が円周上を一定の速度で動いているということは，横軸を時間にすることもできます。例えば点\( \ \mathrm {P} \ \)が\( \ 0.2 \ \)秒で一周するとしたら，こうなります。

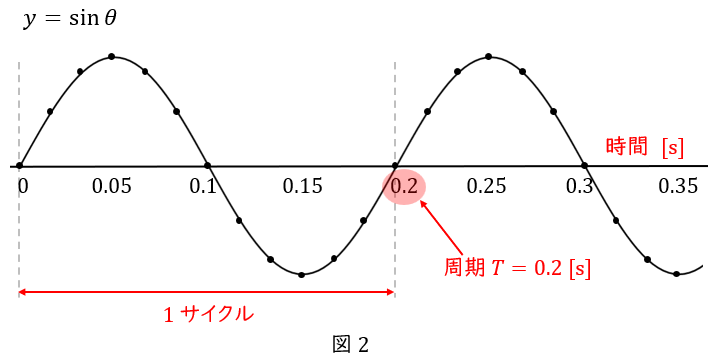
サインカーブの\( \ 1 \ \)サイクル分の時間のことを，周期といいます。記号\( \ T \ \)で表し，電験の場合，単位は秒です。”秒”と漢字で書くより，\( \ \mathrm {second} \ \)の”\( \ \mathrm {s} \ \)”と書かれるので覚えておいてください。

したがって図\( \ 2 \ \)の場合は周期は\( \ 0.2 \ \)秒，式で書くと\( \ T=0.2 \ \mathrm {[s]} \ \)となります。

周波数

\( \ 1 \ \)サイクルにかかる時間よりも，決められた時間に何サイクル現れるかを知りたい場合があり，これを周波数と言います。記号は小文字の\( \ f \ \)で表し，英語の\( \ \mathrm {Frequency} \ \)（頻度）に由来します。
電験の場合，決められた時間とは\( \ 1 \ \)秒間で，下図でいえば，\( \ 1 \ \)秒間に\( \ 5 \ \)サイクル（波が\( \ 5 \ \)個）ありますね。

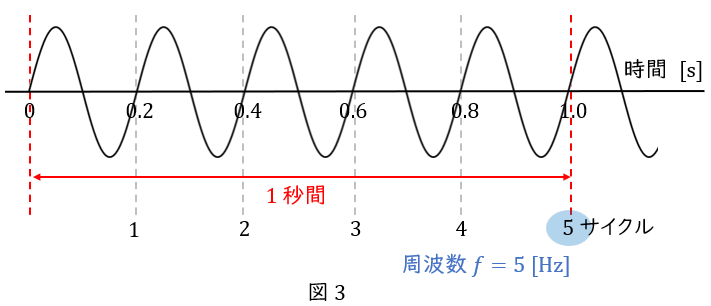
単位は，\( \ 1 \ \)秒間に何サイクルかですから「サイクル/ \( \ \mathrm {s} \ \)」や，\( \ 1 \ \)秒間に現れる波の数で「個/ \( \ \mathrm {s} \ \)」なのですが，これを表す単位である\( \ \mathrm {Hz} \ \)を使います。
読み方はヘルツで，ドイツの物理学者の名前が由来です。

したがって図\( \ 3 \ \)の場合は周波数は\( \ 5 \ \)ヘルツで，式で書くと\( \ f=5 \ \mathrm {[Hz]} \ \)となります。

ちなみに\( \ \mathrm {Hz} \ \)なのにヘルズではなくヘルツなので注意しましょう。自動車の\( \ \mathrm {MAZDA} \ \)（マツダ）やポン酢の\( \ \mathrm {mizkan} \ \)（ミツカン）みたいですね。

以上より，図\( \ 3 \ \)のサインカーブは，
「周期\( \ 0.2 \ \)秒のサインカーブ」とも言えますし，「周波数\( \ 5 \ \)ヘルツのサインカーブ」とも言えます。式で書けば，\( \ T=0.2 \ \mathrm {[s]} \ \)，\( \ f=5 \ \mathrm {[Hz]} \ \)です。

「周期＝波\( \ 1 \ \)個分が何秒か」であり，「周波数＝\( \ 1 \ \)秒間に波が何個か」ですから，\( \ 1 \ \)を周期で割り算すれば，周波数になります。

\[
\begin{eqnarray}
f=\displaystyle \frac{1}{T} \\[ 5pt ] \end{eqnarray}
\]

つまり，周期と周波数は逆数の関係にあって，どちらかが分かれば，もう一方は逆数を計算したら分かるというわけです。周波数から周期を計算することもできます。

\[
\begin{eqnarray}
T=\displaystyle \frac{1}{f} \\[ 5pt ] \end{eqnarray}
\]

回転数

回転運動において，一定時間に回る回数のことです。一定時間とは電験の場合たいてい\( \ 1 \ \)秒間です。記号\( \ n \ \)で表し，単位は\( \ \mathrm {[Hz]} \ \)です。周波数の単位と同じですね。波や振動の場合は周波数，回転運動の場合は回転数というわけです。
「周期＝\( \ 1 \ \)回転が何秒か」であり，「回転数＝\( \ 1 \ \)秒間に何回転か」ですから，回転数は，\( \ 1 \ \)を周期で割り算すれば計算できます。

\[
\begin{eqnarray}
n=\displaystyle \frac{1}{T} \\[ 5pt ] \end{eqnarray}
\]

この関係も周波数と同じですね。

角速度（角周波数・角振動数）

角速度は，その名の通り「角度の速度」つまり「一定時間にどれくらいの角度，移動するか」です。一定時間とは電験では\( \ 1 \ \)秒のことです。
まずは単位円上を動く点\( \ \mathrm {P} \ \)で考えましょう。例えば\( \ 0.2 \ \)秒で一周するとします。円の一周分の角度は弧度法で\( \ 2 \pi \ \)ですから，\( \ 1 \ \)秒間に進む角度はこれを\( \ 0.2 \ \)秒で割るだけです。

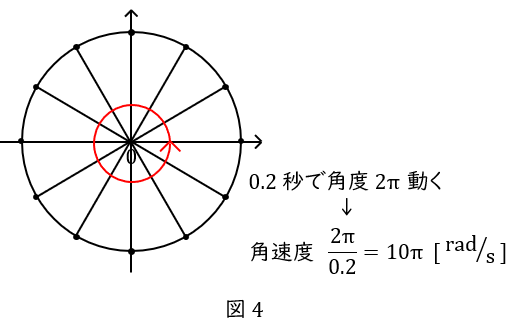
単位は，角度の単位であるラジアン（\( \ \mathrm {rad} \ \)）と，秒（\( \ \mathrm {s} \ \)）で，\( \ \mathrm {[rad/s]} \ \)です。
そして角速度の単位は\( \ \omega \ \)（読み方はオメガ）です。

以上より，点\( \ \mathrm {P} \ \)の角速度は\( \ \omega=10 \pi \ \mathrm {[rad/s]} \ \)です。

今度はこちらのサインカーブで角速度を考えましょう。

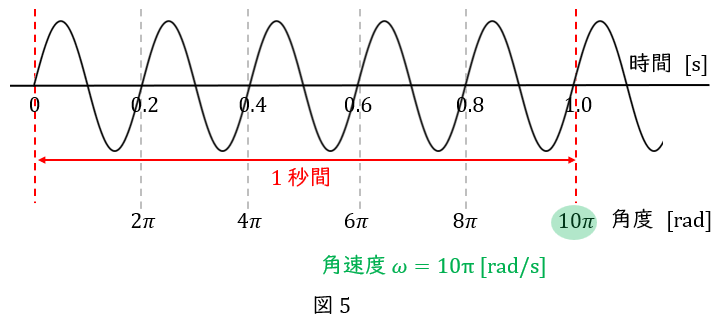
横軸が時間なので，一見，角度の情報がないように思えます。

しかし，サインカーブは，単位円の円周上を，一定の速度で動く点\( \ \mathrm {P} \ \)の，\( \ y \ \)座標を取り出したものとします。

点\( \ \mathrm {P} \ \)が円を一周したら，つまり角度\( \ 2 \pi \ \)だけ動いたら，波が\( \ 1 \ \)つできるのですから，波\( \ 1 \ \)個が角度\( \ 2 \pi \ \)です。
よって横軸を時間から角度に変えると，\( \ 2 \pi,4 \pi,6 \pi,\cdots, 10 \pi \ \)となります（図\( \ 5 \ \)下部）。
\( \ 1 \ \)秒間に角度\( \ 10 \pi \ \)ですから，角速度\( \ \omega=10 \pi \ \mathrm {[rad/s]} \ \)です。

※角速度・角周波数・角振動数の用語について
ややこしいこれらの用語は，同じ意味と考えるのが分かりやすく，差し支えないと思います。
正確には，コイルなどの回転運動では角速度，交流電源の電圧など周期的な振動や波の問題では角周波数や角振動数，と使い分けがあります。しかし，受験生が問題を解くときに気にする必要はないでしょう。角周波数や角振動数よりは，角速度がもっともとっつきやすいので，本ページでは角速度に統一します。

※\( \ \omega \ \)について
\( \ \omega \ \)は，オメガというギリシャ文字の小文字です。オメガの大文字はというと，形がガラリと変わって”\( \ \Omega \ \)”です。抵抗の単位ですね。こちらはオメガとは読まず，オームと読みます。大文字のオメガ\( \ \Omega \ \)をオメガと読むのは高級腕時計のときですね。

角速度と時間の関係

角速度\( \ \omega \ \)は\( \ 1 \ \)秒間に進む角度ですから，\( \ t \ \)秒間で進む角度\( \ \theta \ \)は次のように表せます。

\[
\begin{eqnarray}
\theta=\omega \times t \\[ 5pt ] \end{eqnarray}
\]

角速度の定義を考えれば，\( \ \omega=\displaystyle \frac{\theta}{t} \ \)ですから，それを変形しただけですね。

角速度と周波数の関係

角速度と周波数にはこちらの関係があります。この式は必ず覚えてください。

\[
\begin{eqnarray}
\omega=2 \pi f \\[ 5pt ] \end{eqnarray}
\]

この式を導くには，\( \ 1 \ \)秒に\( \ 1 \ \)回転の場合で考えると簡単です。
\( \ 1 \ \)回転なので周波数\( \ f \ \)は\( \ 1 \ \)，角速度\( \ \omega \ \)は\( \ 2\pi \ \)です。

\( \ f \ \)と\( \ \omega \ \)とをイコールで結ぶためには，\( \ f \ \)の方に\( \ 2\pi \ \)をかければよいので，\( \ \omega=2 \pi f \ \)です。
\( \ \omega \ \)に\( \ 2\pi \ \)をかけると，差が開いてしまうので，間違いと分かります。

また，語呂合わせもあるのですが，下ネタなのでご注意ください。

\( \ \omega \ \)がおっぱいの形に似ているので，「\( \ 2 \ \)つのパイがふっくら」で，\( \ \omega=2 \pi f \ \)です。

失礼いたしました。

こちらで，角速度\( \ \omega \ \)を周波数\( \ f \ \)から計算できるようになりました。

もし，周波数\( \ f \ \)が分からず，周期\( \ T \ \)が分かる場合は，\( \ f=\displaystyle \frac{1}{T} \ \)を使って，まず周期\( \ T \ \)を周波数\( \ f \ \)に換算してください。

※\( \ \omega=2 \pi f \ \)と\( \ \omega=\displaystyle \frac{2\pi}{T} \ \)を同時に覚えようとして，混乱して\( \ \omega=2 \pi T \ \)になる…というミスがあります。
私としては，\( \ \omega= \ \)で覚える公式は\( \ \omega=2 \pi f \ \)だけに絞るのがおススメです。

周期・周波数・角速度の関係まとめ

ここまでのまとめです。

周期は\( \ 1 \ \)サイクル（波\( \ 1 \ \)つ）の時間のこと，

周波数は\( \ 1 \ \)秒間のサイクル数（波の数）のこと，

角速度は\( \ 1 \ \)秒間に進む角度のことです。

重要なのはこれら\( \ 3 \ \)つの関係です。

周期と周波数は，すでに説明した通り逆数の関係にあります。

\( \ f=\displaystyle \frac{1}{T} \ \)を覚えておけば問題ありません。

そしてもう\( \ 1 \ \)つは，角速度と周波数の関係で，\( \ \omega=2 \pi f \ \)です。

練習問題

\( \ (1) \ \)　点\( \ \mathrm {P} \ \)が円の円周上を一定の速さで動くとする。周期\( \ 2 \ \mathrm {[s]} \ \)のとき回転数と角速度はいくつか。

\( \ (2) \ \)　西日本の交流電源の周波数は\( \ 50 \ \mathrm {[Hz]} \ \)である。周期と角振動数を求めよ。

\( \ (3) \ \)　ある回路において，角速度が\( \ 100\pi \ \)，電圧と電流の位相差が\( \ \displaystyle \frac{\pi}{2} \ \)であった。このとき位相差を時間に換算するといくつか。