位相が”遅れる”,”進む”について解説します。これが,サインカーブにおいて最も理解しにくいところかもしれません。
というのも,位相の”遅れる”,”進む”は,第一印象と逆なのです。つまり,位相が”遅れた”ときの波は進んでいるように見え,位相が”進んだ”ときの波は遅れているように見えます。
非常に厄介ですが,正しく覚える方法を解説しますので,最後まで読めば,もう間違えないでしょう。
Contents
位相とは
位相とは,「周期的な運動をするものが,今どのタイミングにあるのかを,角度で表したもの」です。図を見る方が分かりやすいでしょう。
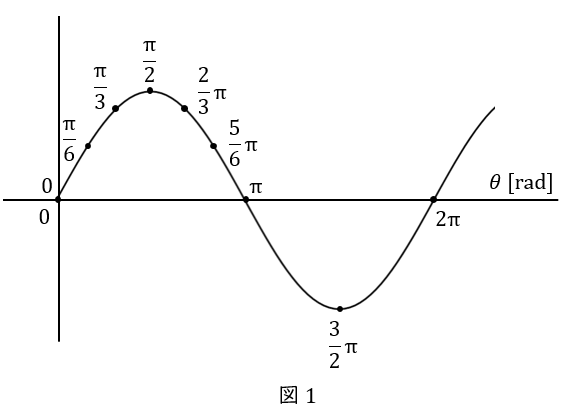
こちらのサインカーブのように,\( \ y=0 \ \)で,しかもこの後に最大値に向かう\( \ 0 \ \)の点を位相\( \ 0 \ \)と定義した場合について述べます。
\( \ y \ \)が最大値の点は,位相\( \ \displaystyle \frac{\pi}{2} \ \)
\( \ y=0 \ \)で,しかもこの後に最小値に向かう\( \ 0 \ \)の点は,位相\( \ \pi \ \),
\( \ y \ \)が最小値の点は,\( \ \displaystyle \frac{3}{2} \pi \ \),
そして再び\( \ y=0 \ \)になり,この後に最大値に向かう\( \ 0 \ \)の点は,位相\( \ 2 \pi \ \)です。
このように,位相は周期的な運動をするものについて,今はどのタイミングかを,角度で表したものです。単位はもちろん,角度と同じラジアン(\( \ \mathrm {rad} \ \))です。
式でいうと,サインの中身です。つまり,\( \ y= \sin\theta \ \)でいう,\( \ \theta \ \)が位相です。
\( \ y= \sin\theta \ \)を,時間\( \ t \ \)を使った式に書き換えよう
ここまでサインカーブの中身は角度\( \ \theta \ \)でしたが,これを時間\( \ t \ \)を使った形に書き換えましょう。
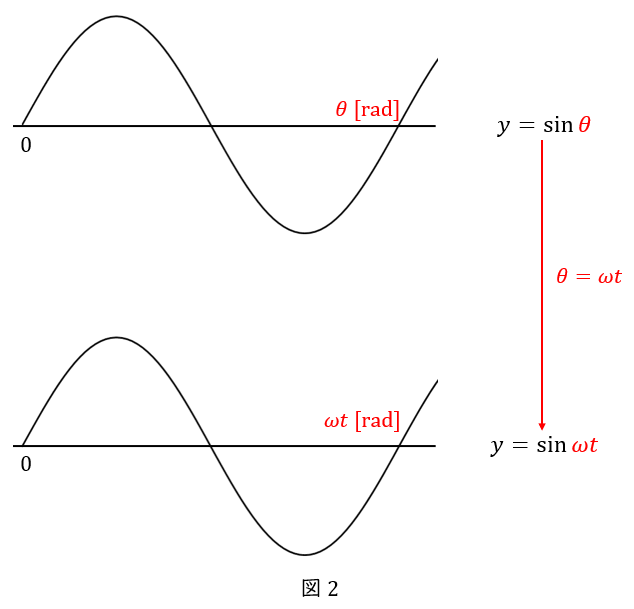
角度\( \ \theta \ \)と時間\( \ t \ \)の関係が分かればよいので,スタートから\( \ t \ \)秒後の角度\( \ \theta \ \)がどうなるかを考えます。
スタートから\( \ t \ \)秒後の角度\( \ \theta \ \)は,\( \ 1 \ \)秒間に進む角度に\( \ t \ \)をかけたものです。
そして”\( \ 1 \ \)秒間に進む角度”とは,角速度\( \ \omega \ \)のことですから
\[
\begin{eqnarray}
\theta=\omega t \\[ 5pt ]
\end{eqnarray}
\]
角度\( \ \theta \ \)と時間\( \ t \ \)の関係が分かりました。
\( \ y= \sin\theta \ \)に,\( \ \theta=\omega t \ \)を代入して,
\[
\begin{eqnarray}
y=\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
この場合も,サインの中身が位相です。\( \ y=\sin \omega t \ \)なら,\( \ \omega t \ \)が位相です。
位相はどれだけずれている?
黒い波と赤い波は,周期は同じですが,ずれています。
どれだけずれているかを位相で表しましょう。
今は遅れている・進んでいるかは気にせず,差だけを考えましょう。
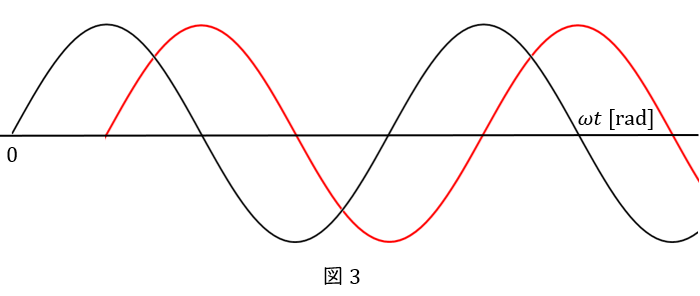
例えば①の時点で考えましょう。
黒い波は最大値なので,位相は\( \ \displaystyle \frac{\pi}{2} \ \)です。
赤い波は\( \ 0 \ \)で,しかもこの後に最大値に向かう\( \ 0 \ \)ですから,位相は\( \ 0 \ \)です。
したがって,黒い波と赤い波の位相差は\( \ \displaystyle \frac{\pi}{2} \ \)です。
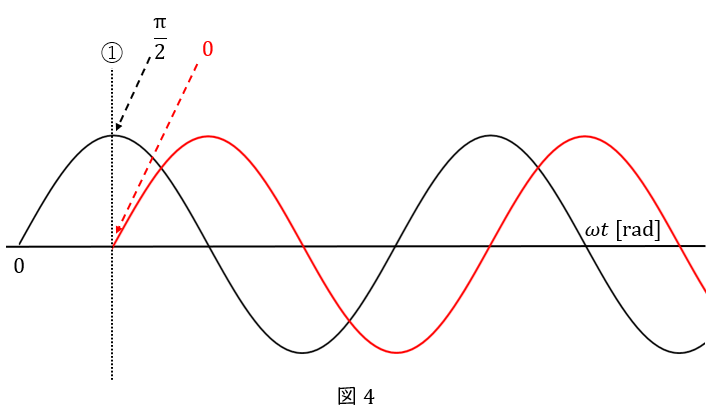
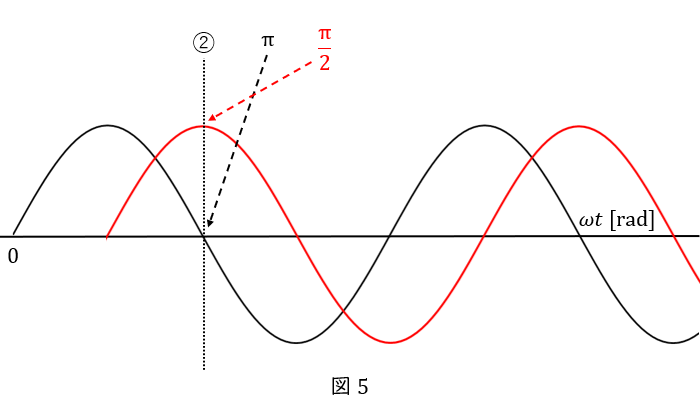
別の時点で考えても構いません。例えば②の時点で考えてみましょう。
黒い波は\( \ 0 \ \)で,しかもこの後に最小値に向かう\( \ 0 \ \)ですから,位相は\( \ \pi \ \)です。
赤い波は最大値なので,位相は\( \ \displaystyle \frac{\pi}{2} \ \)です。
したがって,黒い波と赤い波の位相差は\( \ \displaystyle \frac{\pi}{2} \ \)です。
位相は進んでいる?遅れている?
ここが間違えやすいので,丁寧にいきましょう。赤い波は,黒い波に対して進んでいるでしょうか?遅れているでしょうか?
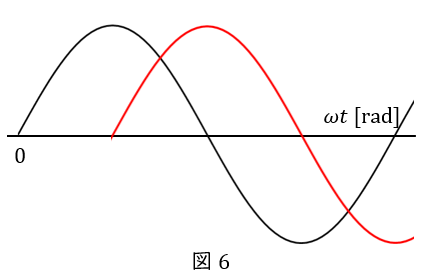
第一印象では”進んでいる”ように見えますよね。でも,そうではないのです。
横軸は\( \ \omega t \ \)ですから,時間が経過するほど,横軸を右に進みます。
あなたが小さくなって原点に立ち,右に進むベルトコンベアーにでも乗ったと考えてください。
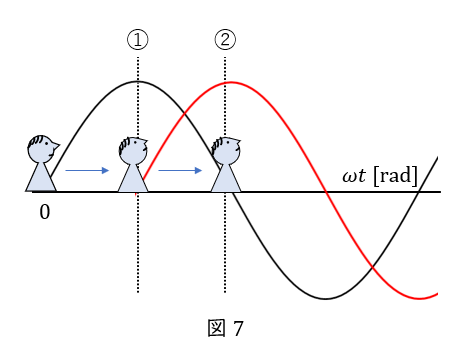
①まで来たとき,黒い波が最大値を迎えました。
そのあと,②まで来たとき,赤い波が最大値を迎えました。
つまり,赤い波の最大値は,黒い波より後でやってくるのです。
したがって,赤い波は黒い波より遅れています。
どれだけの差があるかというと,前に述べた通り,\( \ \displaystyle \frac{\pi}{2} \ \)です。
以上より,赤い波は黒い波より\( \ \displaystyle \frac{\pi}{2} \ \)だけ”遅れて”います。
位相の”進む”,”遅れる”は,あなたが小さくなって原点に立ち,右に進むと考えてください。
そうすれば,もう間違えることはないでしょう。
”位相が遅れる”は式でどうかく?
黒い波が,\( \ y=\sin \omega t \ \)とかけるとき,赤い波はどんな式でかけるでしょうか?
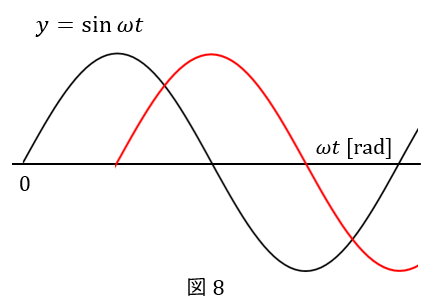
赤い波は,黒い波より\( \ \displaystyle \frac{\pi}{2} \ \)遅れているのですから,
\( \ y=\sin \left(\omega t+ \displaystyle \frac{\pi}{2}\right)\ \)か,\( \ y=\sin \left(\omega t- \displaystyle \frac{\pi}{2}\right)\ \)のどちらかだと予想できます。
どちらか分かるでしょうか?
「遅れるのだからマイナス」とすぐに分かる方は,大丈夫です。以下の説明は飛ばして,練習問題に進んでください。
分からない方は,こう考えてみてください。
赤い波は,黒い波と同じ位相に到達するのに,時間がかかる
時間がかかるとは,\( \ t \ \)を大きくしなければならないということ
なぜ\( \ t \ \)を大きくしなければならないかというと,\( \ \displaystyle \frac{\pi}{2} \ \)が”引き算”されているから
したがって,赤い波は\( \ y=\sin \left(\omega t- \displaystyle \frac{\pi}{2}\right)\ \)です。
まだしっくりこない方は,具体的な数値を入れて考えましょう。
分からないときは具体的な数値を代入するのが一番です。
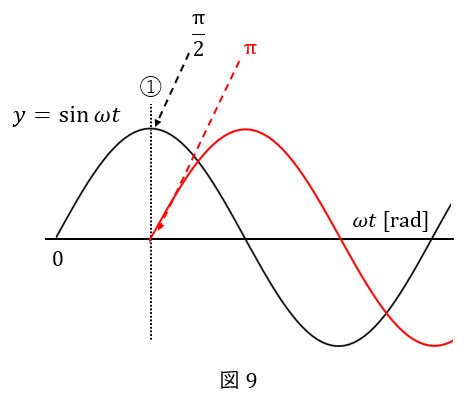
例えば①の時点を考えましょう。
黒い波は最大値なので位相は\( \ \displaystyle \frac{\pi}{2} \ \)です。
黒い波の式は\( \ y=\sin \omega t \ \)ですから,\( \ \omega t = \displaystyle \frac{\pi}{2} \ \)ということです。
一方,赤い波は\( \ 0 \ \)で,このあと最大値に向かう\( \ 0 \ \)ですから,位相は\( \ 0 \ \)になるはずです。
赤い波の位相は,\( \ \omega t+\displaystyle \frac{\pi}{2}\ \)か,\( \ \omega t-\displaystyle \frac{\pi}{2}\ \)のどちらかですが,
\( \ \omega t = \displaystyle \frac{\pi}{2} \ \)を代入して,\( \ 0 \ \)になるのは,\( \ \omega t-\displaystyle \frac{\pi}{2}\ \)の方です。
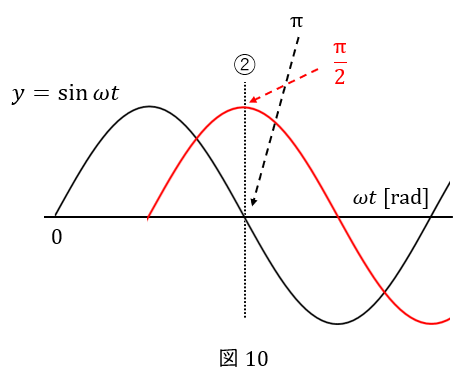
②の時点で考えても同じです。
黒い波は\( \ 0 \ \)で,この後最小値に向かう\( \ 0 \ \)なので,位相は\( \ \pi \ \)です。
黒い波の式は\( \ y=\sin \omega t \ \)ですから,\( \ \omega t = \pi \ \)ということです。
一方,赤い波は最大値ですから,位相は\( \ \displaystyle \frac{\pi}{2} \ \)になるはずです。
赤い波の位相は,\( \ \omega t +\displaystyle \frac{\pi}{2}\ \)か,\( \ \omega t -\displaystyle \frac{\pi}{2}\ \)のどちらかですが,
\( \ \omega t = \pi \ \)を代入して,\( \ \displaystyle \frac{\pi}{2} \ \)になるのは,\( \ \omega t -\displaystyle \frac{\pi}{2} \ \)の方です。
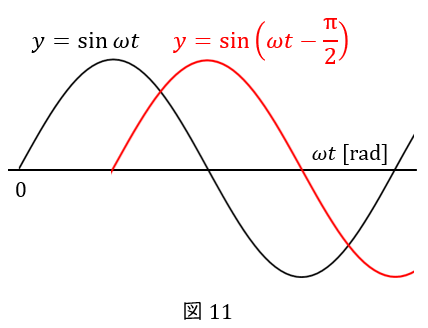
以上をまとめると,波が右側にある場合は,位相は”遅れて”いて,サインの中身にマイナスが付きます。
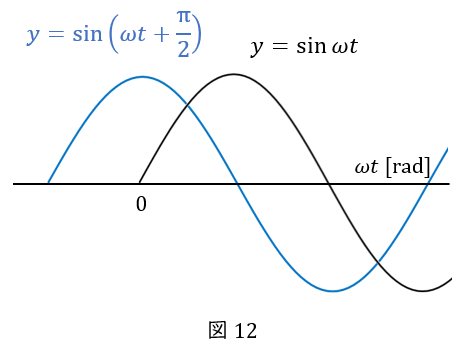
波が左側にあるときは位相が進んでいる
波が左側にある場合は,その逆です。位相は”進んで”いて,サインの中身にプラスが付きます。
位相の進み・遅れの覚え方
以上をまとめたものがこちらです。
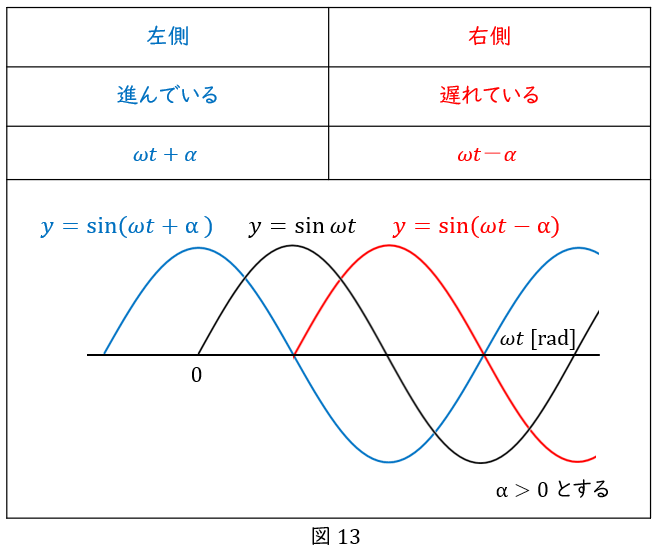
なお,\( \ \omega t \ \)の後に続く\( \ + \alpha \ \)や\( \ – \alpha \ \)のことを”初期位相”と言います。
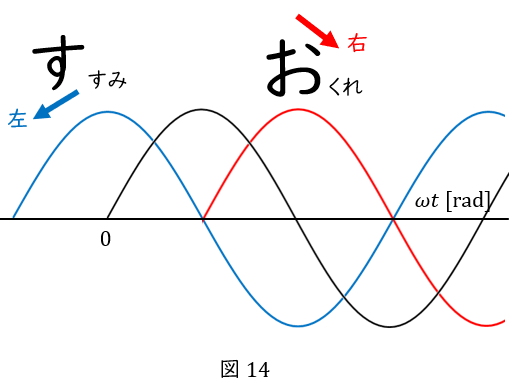
最後に,“左が進み,右が遅れ”の覚え方を紹介します。
”すすむ”の”す”の文字を書くとき,最後は左に払うので,左が”進み”です。
“おくれ”の”お”の文字を書くとき,最後の点は右に向かってうつので,右が”遅れ”です。
練習問題
\( \ (1) \ \) \( \ y=\cos \omega t \ \)を,\( \ \sin \ \)の位相をずらした形で書き換えよ
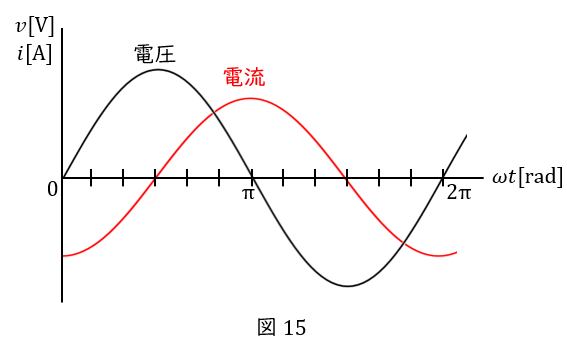
\( \ (2) \ \) 交流電圧をコイルのみの回路に加えると,回路に流れる電流は下図のようになる。このとき,電流は電圧に対してどれだけ遅れているまたは進んでいるか答えよ。
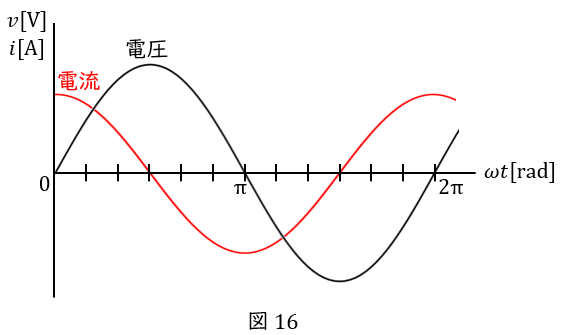
\( \ (3) \ \) 交流電圧をコンデンサのみの回路に加えると,回路に流れる電流は下図のようになる。このとき,電流は電圧に対してどれだけ遅れているまたは進んでいるか答えよ。
\( \ (1) \ \) \( \ y= \sin \left(\omega t +\displaystyle \frac{\pi}{2}\right) \ \)
三角関数③の図\( \ 23 \ \)で紹介した通り,コサインカーブは\( \ 1 \ \)からスタートして,\( \ 0 \ \)を経由して\( \ -1 \ \)に向かいます。
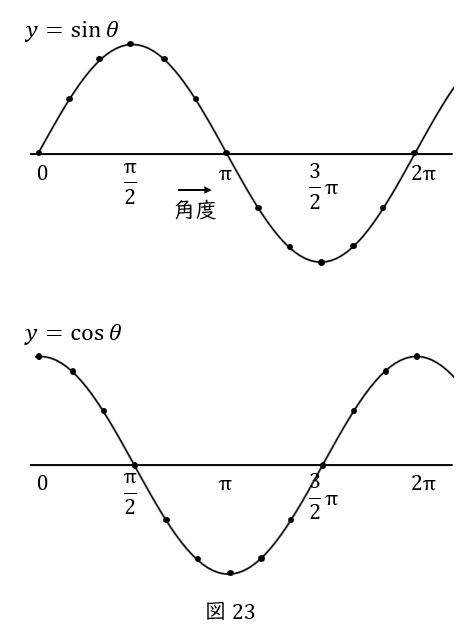
これは,サインカーブを左に\( \ \displaystyle \frac{\pi}{2} \ \)だけ動かしたものと同じです。
つまり,\( \ y=\cos \omega t = \sin \left(\omega t +\displaystyle \frac{\pi}{2}\right) \ \)です。
※サインカーブとはよく聞きますが,コサインカーブって聞き馴染みがありませんよね。それは,この問題から分かる通り,コサインカーブも,サインカーブを使って描くことができるため,あまり使われないのです。
\( \ (2) \ \) 電流は\( \ \displaystyle \frac{\pi}{2} \ \)だけ遅れている。
図\( \ 15 \ \)より,電流は電圧よりも右にありますから,「遅れ」です。どれだけ遅れているかというと,最大値をとるときの横軸の値に注目して,電圧は\( \ \displaystyle \frac{\pi}{2} \ \),電流は\( \ \pi \ \)ですから,その差は\( \ \displaystyle \frac{\pi}{2} \ \)です。
※コイルで,電圧→電流の順であることは,このように覚えましょう。コイルに電流を流し始めた直後,電流の流れを邪魔する起電力(誘導起電力)が働きます。ですから,コイルでは電圧→電流の順です。
\( \ (3) \ \) 電流は\( \ \displaystyle \frac{\pi}{2} \ \)だけ進んでいる。
図\( \ 16 \ \)より,電流は電圧よりも左にありますから,「進み」です。どれだけ進んでいるかというと,最大値をとるときの横軸の値に注目して,電圧は\( \ \displaystyle \frac{\pi}{2} \ \),電流は\( \ 0 \ \)ですから,その差は\( \ \displaystyle \frac{\pi}{2} \ \)です。
※コンデンサで,電流→電圧の順であることは,このように覚えましょう。コンデンサは電荷をためることができます。電荷をためることで徐々に電圧が生じますので,コンデンサでは電流→電圧の順です。


