三角関数 宮崎真以子

【三角関数⑥】交流電源の電圧・電流の瞬時値を式で表そう。複雑な式をスモールステップで丁寧に解説

サインカーブについて分かってきたところで，交流のある瞬間の電圧が，どのような式で表せるかを考えます。
ある瞬間の値のことを瞬時値というので，電圧の瞬時値を\( \ v \ \)として，\( \ v= \ \)の式がどのような形になるかを考えます。

※誘導起電力の場合は，瞬時値\( \ e \ \)と表します。

※\( \ v(t) \ \)や\( \ e(t) \ \)と書かれる場合もあります。\( \ (t) \ \)と書くことで，時間\( \ t \ \)の関数であることを分かりやすくしているのです。

最大振幅

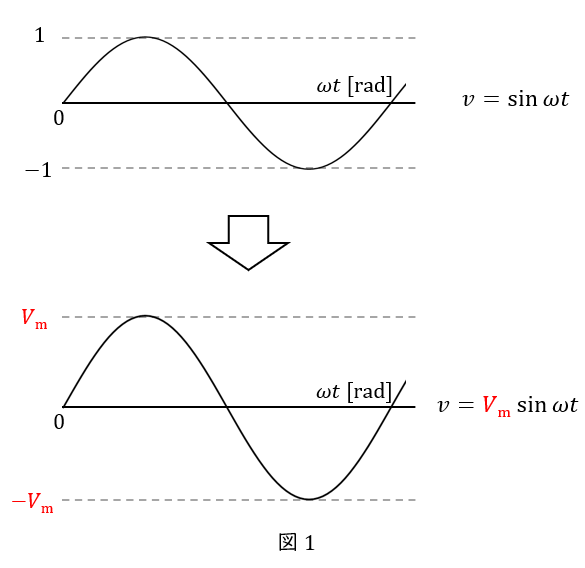
これまでの\( \ y=\sin \omega t \ \)では，最大値は\( \ 1 \ \)で，最小値は\( \ -1 \ \)のサインカーブでした。これを，実際の交流の式にするには，サインの前に最大値をかけるだけです。
つまり交流の電圧の最大値を\( \ V_{\mathrm {m}} \ \)とすると，瞬時値は\( \ v=V_{\mathrm {m}}\sin \omega t \ \)となります。

※誘導起電力の場合，最大値は\( \ E_{\mathrm {m}} \ \)と表します。

初期位相

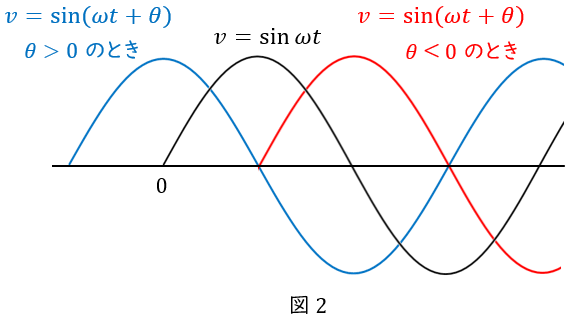
初期位相を\( \ \theta \ \)とすると，\( \ v=V_{\mathrm {m}}\sin (\omega t+\theta) \ \)です。（三角関数⑤参照）。
\( \ \theta \ \)が正の値の場合は位相が進んでおり，グラフは左側にずらした形，\( \ \theta \ \)が負の値の場合は位相が遅れており，グラフは右側にずらした形になります。

電圧の瞬時値\( \ v \ \)

以上より，電圧の瞬時値\( \ v \ \)は下式です。

\[
\begin{eqnarray}
v=V_{\mathrm {m}}\sin (\omega t+\theta)\\[ 5pt ] \end{eqnarray}
\]

いきなりこの式を見ても分かりませんが，今解説した通り一つ一つ組み立てていけば分かります。
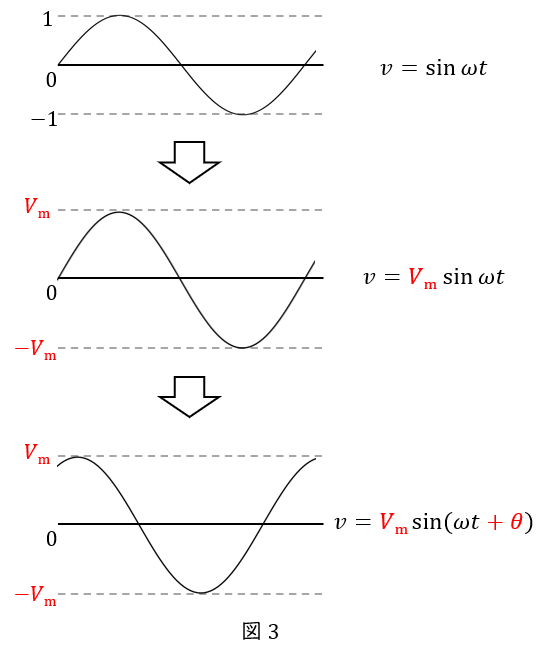
① まずは基本形　\( \ v=\sin \omega t \ \)

② 最大値（振幅）を\( \ V_{\mathrm {m}} \ \)として　\( \ v= V_{\mathrm {m}}\sin \omega t \ \)

③ 初期位相を\( \ \theta \ \)として　\( \ v=V_{\mathrm {m}}\sin (\omega t+\theta) \ \)

④ 以上より，電圧の瞬時値は\( \ v=V_{\mathrm {m}}\sin (\omega t+\theta) \ \)

電流の瞬時値\( \ i \ \)

電流についても同様に，瞬時値\( \ i \ \)を表すことができ，
\( \ i=I_{\mathrm {m}}\sin (\omega t+\theta) \ \)となります。

練習問題

\( \ (1) \ \)　交流の電圧が最大値\( \ 100 \ \mathrm {[V]} \ \)，周波数\( \ 50 \ \mathrm {[Hz]} \ \)，初期位相\( \ \displaystyle \frac{\pi}{3} \ \mathrm {[rad]} \ \)のとき，瞬時値\( \ v \ \)を表す式を求めよ。

\( \ (2) \ \)　交流の電流が最大値\( \ 2 \ \mathrm {[A]} \ \)，周期\( \ 0.02 \ \mathrm {[s]} \ \)，初期位相\( \ \displaystyle \frac{\pi}{4} \ \mathrm {[rad]} \ \)のとき，瞬時値\( \ i \ \)を表す式を求めよ

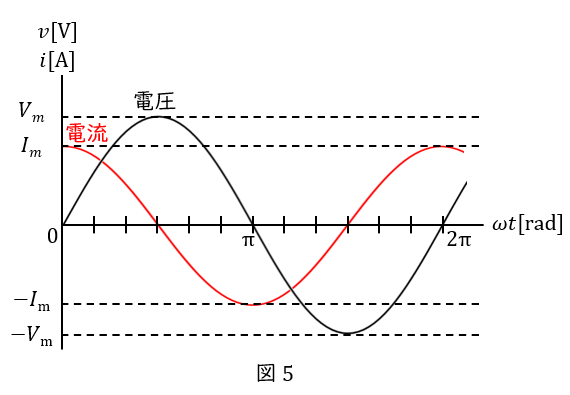
\( \ (3) \ \)　交流電圧をコイルのみの回路に加えると，回路に流れる電流は図のようになる。電圧の瞬時値が\( \ v=V_{\mathrm {m}}\sin \omega t \ \)のとき，電流の瞬時値の式を答えよ。

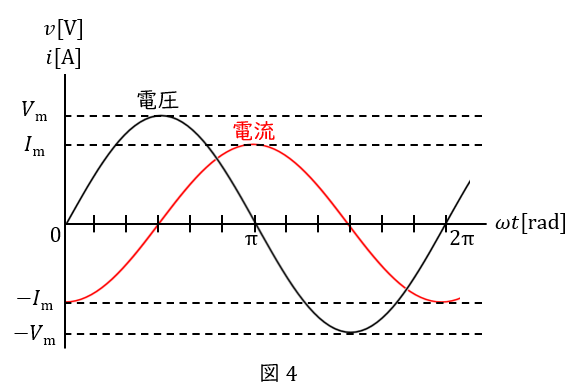
\( \ (4) \ \)　交流電圧をコンデンサのみの回路に加えると，回路に流れる電流は図のようになる。電圧の瞬時値が\( \ v=V_{\mathrm {m}}\sin \omega t \ \)のとき，電流の瞬時値の式を答えよ。

【解答】（クリックして表示）

\( \ (1) \ \)　\( \ v = 100 \sin \left(100 \pi t + \displaystyle \frac{\pi}{3}\right) \ \)

問題文より，
電圧の最大値\( \ V_{\mathrm {m}}=100 \ \mathrm {[V]} \ \)，
周波数\( \ f=50 \ \mathrm {[Hz]} \ \)，
初期位相\( \ \theta=\displaystyle \frac{\pi}{3} \ \mathrm {[rad]} \ \)です。

電圧の瞬時値の式は，\( \ v=V_{\mathrm {m}}\sin (\omega t+\theta) \ \)です。これは何も見ないでかけるようになっておきましょう。

\( \ V_{\mathrm {m}} \ \)と\( \ \theta \ \)は分かるので，あとは\( \ \omega \ \)が分かれば良いですね。

\( \ \omega \ \)の公式と言えば\( \ \omega = 2 \pi f \ \)であり，問題文から\( \ f \ \)は分かっていますので，\( \ \omega = 2 \pi \times 50 = 100 \pi \ \)です。

以上より，\( \ v=V_{\mathrm {m}}\sin (\omega t+\theta)=100 \sin \left(100 \pi t + \displaystyle \frac{\pi}{3}\right) \ \)

\( \ (2) \ \)　\( \ i = 2 \sin \left(100 \pi t + \displaystyle \frac{\pi}{4}\right) \ \)

問題文より，
電流の最大値\( \ I_{\mathrm {m}}=2 \ \mathrm {[A]} \ \)，
周期\( \ T = 0.02 \ \mathrm {[s]} \ \)，
初期位相\( \ \theta=\displaystyle \frac{\pi}{4} \ \mathrm {[rad]} \ \)です。

そして電流の瞬時値の式は，\( \ i=I_{\mathrm {m}}\sin (\omega t+\theta) \ \)です。これは何も見ないでかけるようになっておきましょう。

\( \ I_{\mathrm {m}} \ \)と\( \ \theta \ \)は分かるので，あとは\( \ \omega \ \)が分かれば良いですね。

\( \ \omega \ \)の公式と言えば\( \ \omega = 2 \pi f \ \)ですが，\( \ f \ \)が分かりません。

しかし，\( \ T \ \)なら分かります。\( \ f \ \)と\( \ T \ \)は逆数の関係ですから，

\( \ f =\displaystyle \frac{1}{T} = \displaystyle \frac{1}{0.02}=50 \ \mathrm {[Hz]} \ \)となります。

\( \ \omega = 2 \pi f \ \)に代入して，\( \ \omega = 2 \pi \times 50 = 100 \pi \ \mathrm {[rad/s]} \ \)

以上より，\( \ i =I_{\mathrm {m}}\sin (\omega t+\theta)=2 \sin \left(100 \pi t + \displaystyle \frac{\pi}{4}\right) \ \)

\( \ (3) \ \)　\( \ i = I_{\mathrm {m}} \sin \left(\omega t – \displaystyle \frac{\pi}{2}\right) \ \)

電流が電圧より右にあるので“遅れ”，位相差は\( \ \displaystyle \frac{\pi}{2} \ \)です。遅れなので\( \ \omega t \ \)にマイナスをつけて，\( \ \omega t – \displaystyle \frac{\pi}{2} \ \)です。最大値は図中に\( \ I_{\mathrm {m}} \ \)と書かれているので，\( \ i = I_{\mathrm {m}} \sin \left(\omega t – \displaystyle \frac{\pi}{2}\right) \ \)

\( \ (4) \ \)　\( \ i = I_{\mathrm {m}} \sin \left(\omega t + \displaystyle \frac{\pi}{2}\right) \ \)

電流が電圧より左にあるので“進み”，位相差は\( \ \displaystyle \frac{\pi}{2} \ \)です。進みなので\( \ \omega t \ \)にプラスをつけて，\( \ \omega t + \displaystyle \frac{\pi}{2} \ \)です。最大値は図中に\( \ I_{\mathrm {m}} \ \)と書かれているので，\( \ i = I_{\mathrm {m}} \sin \left(\omega t + \displaystyle \frac{\pi}{2}\right) \ \)



RECOMMENDこちらの記事も人気です。