三角関数の公式はたくさんありますが,ここは”電験合格のため”のサイトですから,電験に出てくる公式だけを紹介します。
\( \ \sin ^{2} \theta + \cos ^{2} \theta = 1 \ \)
実をいうと,これは三平方の定理です。
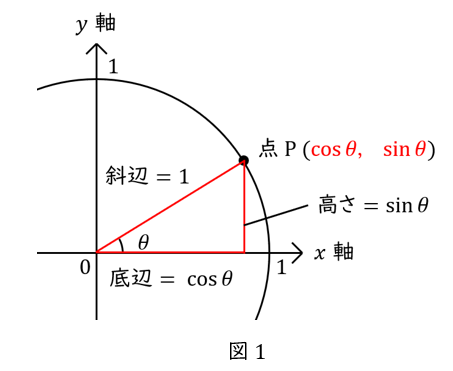
単位円の円周上に点\( \ \mathrm {P} \ \)をとって直角三角形を作ったとき,
高さは\( \ \sin \theta \ \),底辺は\( \ \cos \theta \ \),斜辺の長さは円の半径と同じですから\( \ 1 \ \)ですね。
三平方の定理より,\( \ 底辺^2 + 高さ^2 = 斜辺^2 \ \)なので,\( \ \sin^2 \theta + \cos^2 \theta = 1^2 \ \)
よって,
\[
\begin{eqnarray}
\sin ^{2} \theta + \cos ^{2} \theta &=& 1 \\[ 5pt ]
\end{eqnarray}
\]
加法定理
サイン・コサインの中身の,足し算や引き算を消したいときに使用できる定理です。
実をいうと合格に必須というわけではないのですが,教科書や過去問解説を読んでいると登場するので,紹介しておきます。
合格に必須ではないとする理由は三角関数⑧にて解説します。
\[
\begin{eqnarray}
\sin (A+B) &=& \sin A \cos B + \cos A \sin B \\[ 5pt ]
\sin (A-B) &=& \sin A \cos B – \cos A \sin B \\[ 5pt ]
\end{eqnarray}
\]
覚え方は,呪文のように「シンコスコスシン」です。\( \ + \ \)と\( \ – \ \)の符号はそのままです。
\[
\begin{eqnarray}
\cos (A+B) &=& \cos A \cos B – \sin A \sin B \\[ 5pt ]
\cos (A-B) &=& \cos A \cos B + \sin A \sin B \\[ 5pt ]
\end{eqnarray}
\]
覚え方は,呪文のように「コスコスシンシン」です。\( \ + \ \)と\( \ – \ \)の符号が反転することにご注意ください。
練習例題
\( \ (1) \ \) 電圧と電流の位相差が\( \ \theta \ \)の交流回路について,力率\( \ \cos \theta \ \)が\( \ 0.6 \ \)のとき,無効率\( \ \sin \theta \ \)はいくつか。
\( \ (2) \ \) \( \ 2 \ \)つの電力\( \ P_\mathrm {1} \ \)と\( \ P_\mathrm {2} \ \)が下式で表せるとき,\( \ P_\mathrm {1} + P_\mathrm {2} \ \)はいくつか。
\[
\begin{eqnarray}
P_\mathrm {1} = VI \cos\left( \displaystyle \frac{\pi}{6}+\theta\right) \\[ 5pt ]
P_\mathrm {2} = VI \cos\left( \displaystyle \frac{\pi}{6}-\theta\right) \\[ 5pt ]
\end{eqnarray}
\]
\( \ (1) \ \) \( \ 0.8 \ \)
\( \ \sin^2 \theta + \cos^2 \theta = 1 \ \)に\( \ \cos \theta = \ 0.6 \ \)を代入して,
\[
\begin{eqnarray}
\sin^2 \theta + \cos^2 \theta &=& 1 \\[ 5pt ]
\sin^2 \theta + (0.6)^2 &=& 1 \\[ 5pt ]
\sin^2 \theta &=& 1 – 0.36 = 0.64 \\[ 5pt ]
\sin \theta &=& \sqrt{0.64} = 0.8 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (2) \ \) \( \ \sqrt{3} PV \cos \theta \ \)
\( \ P_\mathrm {1} = VI \cos\left( \displaystyle \frac{\pi}{6}+\theta\right) \ \)はコサインの中身が足し算になっているので,下式の加法定理を利用します。
\[
\begin{eqnarray}
\cos \left( A+B\right) &=& \cos A \cos B – \sin A \sin B \\[ 5pt ]
\cos \left( \displaystyle \frac{\pi}{6}+\theta\right) &=&\cos \frac {\pi }{6} \cos \theta – \sin \frac {\pi }{6} \sin \theta \\[ 5pt ]
&=&\frac{\sqrt{3}}{2} \cos \theta – \frac{1}{2} \sin \theta\\[ 5pt ]
\end{eqnarray}
\]
\( \ P_\mathrm {2} = VI \cos\left( \displaystyle \frac{\pi}{6}-\theta\right) \ \)はコサインの中身が引き算になっているので,下式の加法定理を利用します。
\[
\begin{eqnarray}
\cos (A-B) &=& \cos A \cos B + \sin A \sin B \\[ 5pt ]
\cos \left( \displaystyle \frac{\pi}{6}-\theta\right) &=&\cos \frac{\pi}{6} \cos \theta + \sin \frac{\pi}{6} \sin \theta \\[ 5pt ]
&=&\frac{\sqrt{3}}{2} \cos \theta + \frac{1}{2} \sin \theta\\[ 5pt ]
\end{eqnarray}
\]
したがって,\( \ P_\mathrm {1} + P_\mathrm {2} \ \)は,
\[
\begin{eqnarray}
P_\mathrm {1} + P_\mathrm {2} &=& PV \left(\frac{\sqrt{3}}{2} \cos \theta – \frac{1}{2} \sin \theta\right) + PV \left(\frac{\sqrt{3}}{2} \cos \theta + \frac{1}{2} \sin \theta\right)\\[ 5pt ]
&=&PV \left(\frac{\sqrt{3}}{2} \cos \theta \right)+PV \left(\frac{\sqrt{3}}{2} \cos \theta \right)\\[ 5pt ]
&=&PV \cdot \sqrt{3} \cos \theta \\[ 5pt ]
&=&\sqrt{3} PV \cos \theta \\[ 5pt ]
\end{eqnarray}
\]


