【三角関数⑧】電験に出てくる三角比・三角関数の問題を理解しよう。

実際に電験の問題において，三角比・三角関数がどのように出題されるかを確認しましょう。

トルク\( \ T = F D \cos \theta \ \)

トルクは回転力のことです。
棒を回転させるのは，棒にかけた力\( \ F \ \)（黒矢印）のうち，回転軸に対して垂直な成分です（赤矢印）。
棒の角度を\( \ \theta \ \)と定義すると，図の青い角も\( \ \theta \ \)となるので，赤矢印の大きさは\( \ F \cos \theta \ \)です。

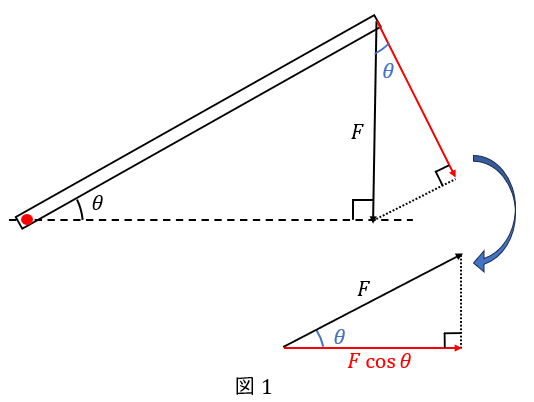
加えて，回転力は腕の長さ\( \ D \ \)にも比例するため，トルク\( \ T \ \)はこの式になります。

\[
\begin{eqnarray}
T = F \cos \theta \times D = F D \cos \theta \\[ 5pt ] \end{eqnarray}
\]

誘導起電力\( \ e = B l v \sin \theta \ \)

導体が磁場中を移動すると起電力を生じます。しかし，起電力を生じるのは磁場に垂直方向の動きだけなので，図の角を\( \ \theta \ \)と定義すると，起電力に寄与する速度は\( \ v \sin \theta \ \)です。

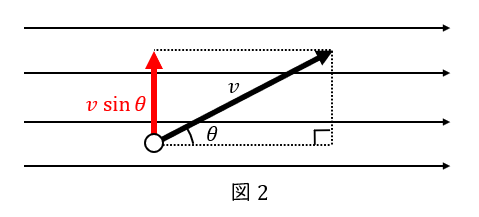
加えて，誘導起電力は磁束の密度\( \ B \ \)と導体の長さ\( \ l \ \)にも比例するため，誘導起電力\( \ e \ \)はこの式になります。

\[
\begin{eqnarray}
e = v \sin \theta \times B l = B l v \sin \theta \\[ 5pt ] \end{eqnarray}
\]

有効電力\( \ P = VI \cos \phi \ \)

交流の負荷（簡単に言えば，交流回路につなぐもの）として，抵抗・コイル・コンデンサがありますが，一般にいう電力を消費するのは抵抗だけです。
抵抗では，電気エネルギーを熱エネルギーに変換するなどして，電力を消費します。このように消費された電力のことを有効電力と言います。

そして，抵抗では電圧と電流が同位相です。
したがって，有効電力を求めるには，電圧と電流の大きさのうち，同じ方向の成分だけに注目して，

\[
\begin{eqnarray}
電力 = 電圧 \times 電流 \\[ 5pt ] \end{eqnarray}
\]

の式に当てはめます。

電圧を基準とするのが一般的ですから，
電流の大きさのうち，電圧と同方向の成分だけ取り出します。
電圧のベクトルと電流のベクトルのなす角を\( \ \phi \ \)とすると，これは\( \ I \cos \phi \ \)となるので，

\[
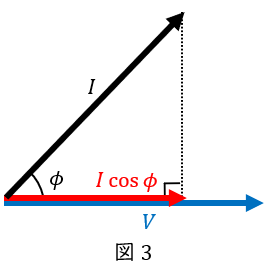
\begin{eqnarray}
有効電力 = 電圧 \times 電流のうち電圧と同じ方向の成分 \\[ 5pt ] \end{eqnarray}
\]

\[
\begin{eqnarray}
P = VI \cos \phi \\[ 5pt ] \end{eqnarray}
\]

となります。

なお，コイルやコンデンサは，電気エネルギーを蓄えたり放出したりするだけで，有効電力を消費しません。

※抵抗は有効電力を消費すること，そしてコイルとコンデンサで有効電力を消費しないことは，実際に計算すると証明できます。瞬時電力\( \ p \ \)を計算して，\( \ 1 \ \)周期の平均値を出すという内容で，この計算の際に三角関数の\( \ 2 \ \)倍角の公式，和積の公式を使用します。しかし，電験三種の合格に，この計算は必須ではないので，本サイトでは割愛します。

※合格のために必要な理解として，「コイルやコンデンサは，電気エネルギーを蓄えたり放出したりするだけだから，有効電力を消費しない」ことをおさえておきましょう

\( \ \mathrm {Y-Y} \ \)結線における線間電圧\( \ V_{\mathrm {ab}} = \sqrt{3} \times \ \)相電圧\( \ E_{\mathrm {ab}} \ \)

※ここからはベクトルを使用します。ベクトルとは，大きさと向きを持つ量のことです。ある量がベクトルであることは，記号の上にドットを付けて表現します。
つまり，\( \ \dot{E_{\mathrm {a}}} \ \)とは\( \ E_{\mathrm {a}} \ \)ベクトルのことです。
また，\( \ \dot{E_{\mathrm {a}}} \ \)の大きさのことを，\( \ E_{\mathrm {a}} \ \)と記載します。

\( \ \mathrm {Y-Y} \ \)結線とは，図のように電源も負荷も\( \ \mathrm {Y} \ \)結線の回路です。

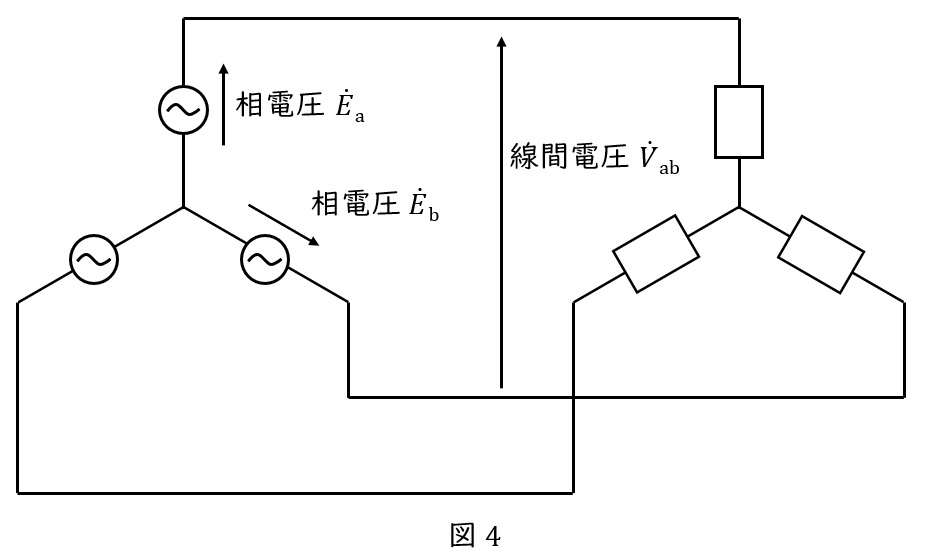
①対称三相交流の場合，\( \ \dot{E_{\mathrm {a}}} \ \)と\( \ \dot{E_{\mathrm {b}}} \ \)の大きさは同じです。

②向きは，\( \ \dot{E_\mathrm {a}} \ \)を基準としたとき\( \ \dot{E_\mathrm {b}} \ \)は\( \ -\displaystyle \frac{2}{3} \pi \ \)です。

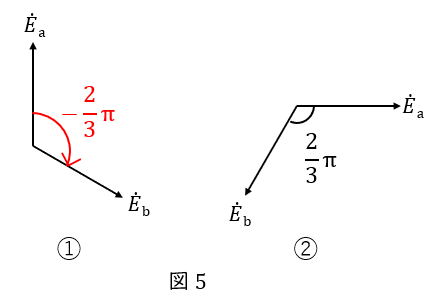
赤矢印の閉ループから次の等式が成立します。

\[
\begin{eqnarray}
\dot{E_\mathrm {a}} -\dot{\ V_\mathrm {ab}} -\dot{E_\mathrm {b}} = 0 \\[ 5pt ] \end{eqnarray}
\]

線間電圧\( \dot{\ V_\mathrm {ab}} = \ \)の形に直すとこちらです。

\[
\begin{eqnarray}
\dot{\ V_\mathrm {ab}} = \dot{E_\mathrm {a}} – \dot{E_\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\]

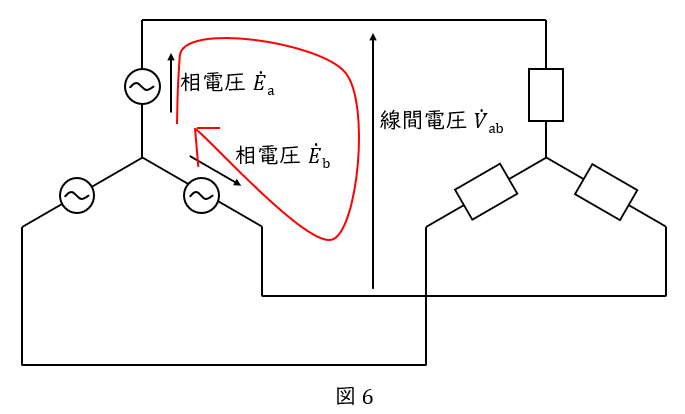
③\( \ \dot{E_\mathrm {b}} \ \)の向きを変えて，\( \ -\dot{E_\mathrm {b}} \ \)とします。このとき\( \ \dot{E_\mathrm {a}} \ \)と\( \ -\dot{E_\mathrm {b}} \ \)のなす角は\( \ \displaystyle \frac{\pi}{3} \ \)となります。

④⑤\( \ \dot{E_\mathrm {a}} \ \)と\( \ -\dot{E_\mathrm {b}} \ \)を足し算である\( \ \dot{V_\mathrm {ab}} \ \)は図の水色矢印となります。

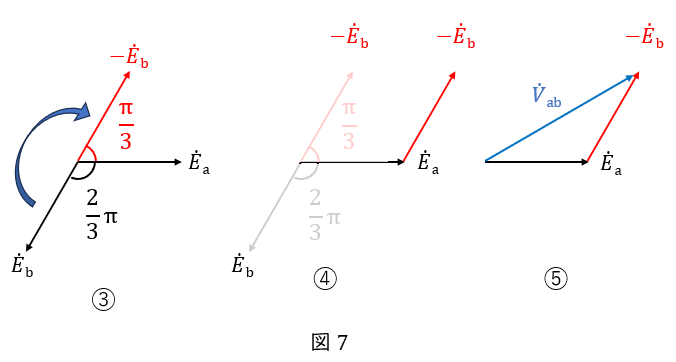
\( \ V_\mathrm {ab} \ \)（つまり\( \ \dot{V_\mathrm {ab}} \ \)の大きさ）を求めるときに，三角比の特別角の知識を使います。

⑥⑦\( \ \dot{E_\mathrm {a}} \ \)と\( \ -\dot{E_\mathrm {b}} \ \)のなす角は下図の通りです。

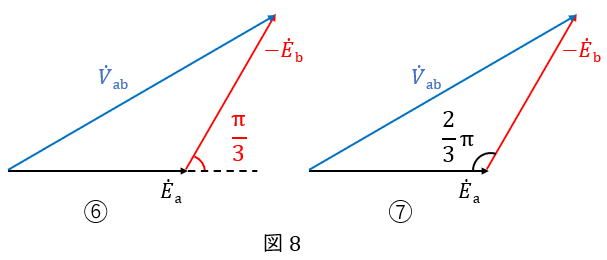
⑧\( \ \dot{E_\mathrm {a}} \ \)の先端から\( \ \dot{V_\mathrm {ab}} \ \)に向かって垂線をおろすことで，直角三角形が\( \ 2 \ \)つくっついた形ができあがります。

⑨⑩\( \ \displaystyle \frac{\pi}{3} \ \)の直角三角形ですから，辺の比は\( \ \displaystyle 1:\frac{1}{2}:\frac{\sqrt{3}}{2} \ \)です。

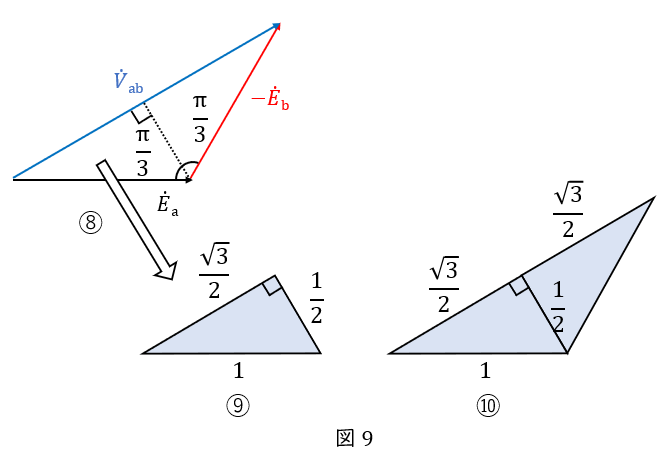
⑪よって，\( \ E_\mathrm {a} \ \)を\( \ 1 \ \)としたとき，\( \ V_\mathrm {ab} \ \)は\( \ \sqrt{3} \ \)となります。

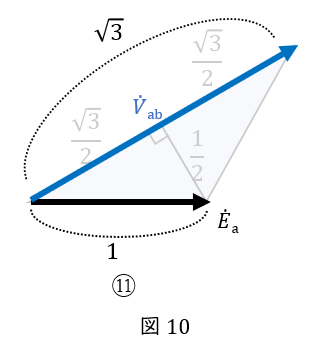
以上より，

\[
\begin{eqnarray}
線間電圧の大きさV_\mathrm {ab}= \sqrt{3} \times 相電圧の大きさE_\mathrm {a} \\[ 5pt ] \end{eqnarray}
\]

となります。

なお，\( \ \mathrm {\Delta-\Delta}\ \)結線における\( \ 線電流の大きさI_{l}= \sqrt{3} \times 相電流の大きさI_{p} \ \)も同様の考え方で算出します。

二電力計法

三相電力の測定方法として，\( \ 2 \ \)つの単相電力計を接続し，それらの指示値の和で三相電力を求めるという方法があります（二電力計法という）。\( \ 2 \ \)つの単相電力計の指示値の和が三相電力となることの証明に，三角関数の加法定理を使用します。
しかしながら，電験三種でこの証明は出題されないと思いますので，こちらだけ覚えておきましょう。

\[
\begin{eqnarray}
三相電力＝ \ 2 \ つの単相電力計の指示値の和 \\[ 5pt ] \end{eqnarray}
\]

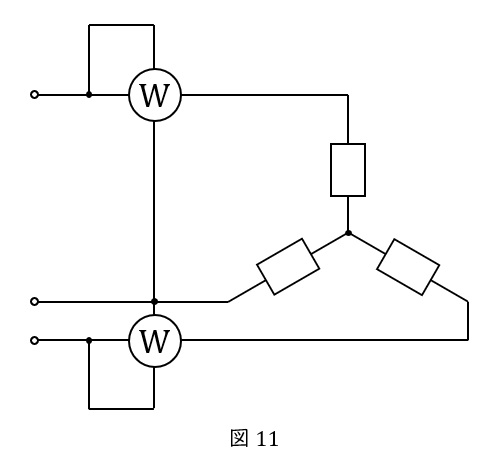
例えばこの回路のように，単層電力計\( \ 2 \ \)つを接続すれば，平行三相負荷の電力が，\( \ 2 \ \)つの単層電力計の指示値の和として求めることができます。

合成電圧

交流電源を複数つないだときの合成電圧を計算するときに，三角関数の加法定理を用いることがあります。しかし，加法定理を逆方向に使用する（下式の右辺から左辺に変形する）ことになるため，難しいです。

\[
\begin{eqnarray}
\sin(A+B) &=& \sin A \cos B + \cos A \sin B \\[ 5pt ] \sin(A-B) &=& \sin A \cos B – \cos A \sin B \\[ 5pt ] \cos(A+B) &=& \cos A \cos B – \sin A \sin B \\[ 5pt ] \cos(A-B) &=& \cos A \cos B + \sin A \sin B \\[ 5pt ] \end{eqnarray}
\]

合成電圧の算出は，極座標と直交座標を使って足し算する方が簡単ですので，そちらを使いましょう。極座標と直交座標については今後解説予定です。