Contents
斜辺・底辺・高さの定義
ひとくちに直角三角形といっても,形も大きさも向きも様々です。
まずは向きを統一しましょう。直角が右下にくるようにします。
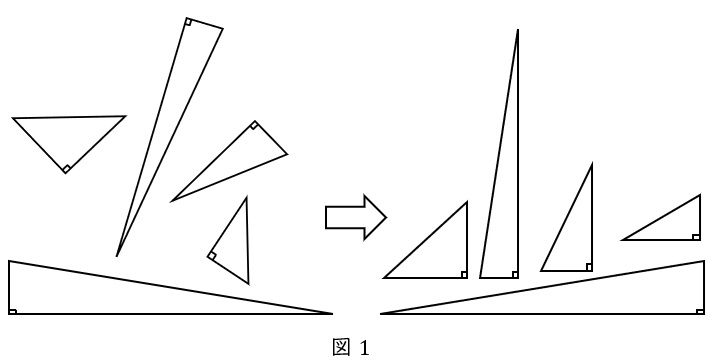
このときに左下にくる角度を\( \ \theta \ \)(シータ)と呼びます。例えば左下の角度が\( \ 20^\circ \ \)であれば, “\( \ \theta=20^\circ \ \)の直角三角形” と表現します。
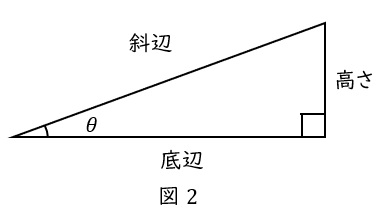
辺の名前は,斜めの一番長い辺が ”斜辺(しゃへん)” ,横の辺が ”底辺” ,縦の辺が ”高さ” です。
※底辺は “隣辺” ,高さは “対辺” とも言いますが,ここでは分かりやすさを重視して,”底辺” と “高さ” とします。
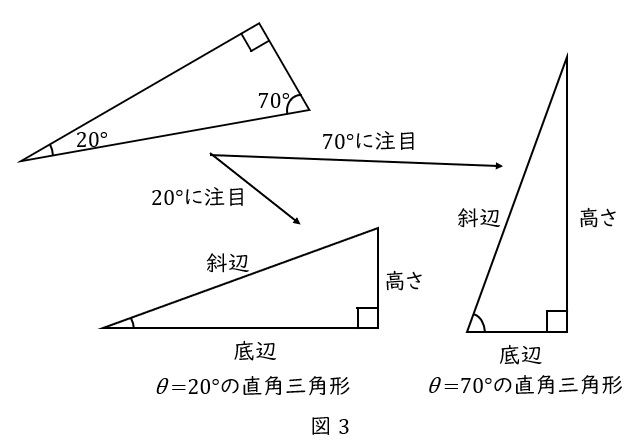
ここで注意したいのが,どの角度を\( \ \theta \ \)とするかで,底辺と高さが変わることです。
同じ三角形を,ひっくり返して置いた場合は,”\( \ \theta=70^\circ \ \)の直角三角形” と表現し,底辺と斜辺も図のように変わります。
斜辺が\( \ 2 \ \)倍,\( \ 3 \ \)倍のとき,高さはどうなる?
ここで,\( \ \theta=20^\circ \ \),斜辺\( \ 2 \ \mathrm {cm} \ \)の直角三角形を一緒に描いてみましょう。分度器も定規も使わず適当でいいです。ノートがなければ,頭の中でも構いません。
ノートの罫線(印刷されている横線)に対して,\( \ 20^\circ \ \)っぽい角度で直線をひき,長さ\( \ 2 \ \mathrm {cm} \ \)っぽいところで止めます。これが斜辺です。そこから真下に線を引き,ノートの罫線と直角になるところで止めます。底辺を書いて,直角三角形のできあがりです。
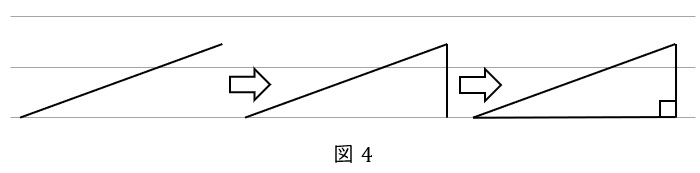
今みなさまは,”高さ” で悩まなかったはずです。つまり,”\( \ \theta \ \)と斜辺が決まっていれば,高さは自動的に決まった” のです。このことは,後ほど解説します。
今度は,\( \ \theta=20^\circ \ \)はそのままで,斜辺を\( \ 2 \ \)倍の\( \ 4 \ \mathrm {cm} \ \)にします。高さはどうなるでしょう?高さも\( \ 2 \ \)倍ですね。
斜辺を\( \ 3 \ \)倍の\( \ 6 \ \mathrm {cm} \ \)にするとどうでしょう。高さも\( \ 3 \ \)倍です。
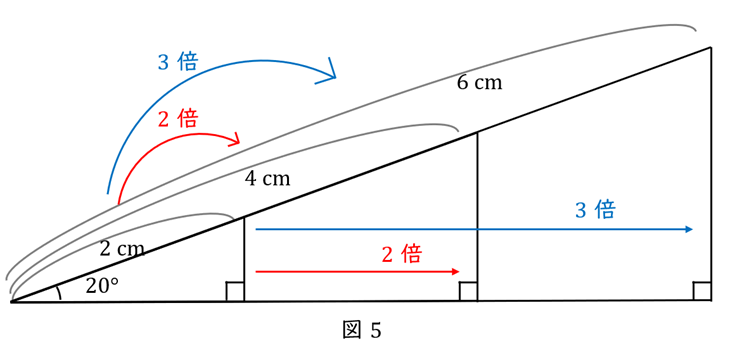
実際の高さはこうなります。
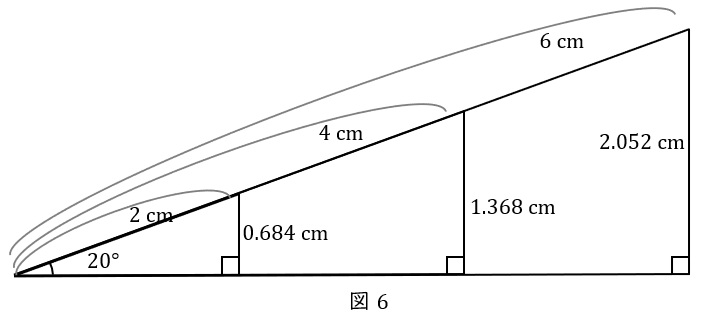
ここで,高さ:斜辺 で比をとると,\( \ 3 \ \)つの三角形はどれも比が同じだと分かります。
斜辺\( \ 2 \ \mathrm {cm} \ \)の三角形の高さ:斜辺\( \ = 0.684:2 = 0.342:1 \ \)
斜辺\( \ 4 \ \mathrm {cm} \ \)の三角形の高さ:斜辺\( \ = 1.368:4 = 0.342:1 \ \)
斜辺\( \ 6 \ \mathrm {cm} \ \)の三角形の高さ:斜辺\( \ = 2.052:6 = 0.342:1 \ \)
三角比とは,辺の長さ:辺の長さ の ”比の値” のこと
みなさまは, ”比の値” という言葉をご存じでしょうか。
小学\( \ 6 \ \)年生くらいで,比と一緒に習っているはずです。といっても,私は覚えていませんでした。
比の値とは,\( \ a:b \ \)で表された比で,\( \ b \ \)を\( \ 1 \ \)とみたときに\( \ a \ \)がいくつになるかです。
要するに,\( \ a:b \ \)の比の値は,\( \ a \div b \ \)です。
例えば, \( \ 3:4 \ \)の比の値は,\( \ 3 \div 4 = 0.75 \ \)です。
同様に, 高さ:斜辺 の比の値は, 高さ\( \ \div \ \)斜辺です。
三角比とは,直角三角形の辺の長さと辺の長さの比の値なのです。
ここで,図\( \ 6 \ \)の\( \ 3 \ \)つの三角形について,比の値を確認しましょう。
斜辺\( \ 2 \ \mathrm {cm} \ \)の三角形の高さ\( \ \div \ \)斜辺\( \ = 0.684 \div 2 = 0.342 \ \)
斜辺\( \ 4 \ \mathrm {cm} \ \)の三角形の高さ\( \ \div \ \)斜辺\( \ = 1.368 \div 4 = 0.342 \ \)
斜辺\( \ 6 \ \mathrm {cm} \ \)の三角形の高さ\( \ \div \ \)斜辺\( \ = 2.052 \div 6 = 0.342 \ \)
比の値が同じです。
この\( \ 3 \ \)つだけでなく,\( \ \theta=20^\circ \ \)の直角三角形ならば,必ず 高さ\( \ \div \ \)斜辺\( \ = 0.342 \ \) となります。
言い換えれば,” \( \ \theta \ \)が決まれば, 高さ\( \ \div \ \)斜辺も決まる” のです。
つまり,辺の長さが分からないのに,辺と辺の比の値だけが分かる,ということですね。
これが,三角比が難しい理由ですが,ご理解いただけましたでしょうか?
【参考:三角比の一覧表】
高さ\( \ \div \ \)斜辺は,\( \ \theta \ \)ごとに決まった値なので,一覧表があります。
確かに\( \ \theta=20^\circ \ \)なら\( \ 0.342 \ \)になっていますね。
| 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.017 | 21 | 0.358 | 41 | 0.656 | 61 | 0.875 | 81 | 0.988 |
| 2 | 0.035 | 22 | 0.375 | 42 | 0.669 | 62 | 0.883 | 82 | 0.990 |
| 3 | 0.052 | 23 | 0.391 | 43 | 0.682 | 63 | 0.891 | 83 | 0.993 |
| 4 | 0.070 | 24 | 0.407 | 44 | 0.695 | 64 | 0.899 | 84 | 0.995 |
| 5 | 0.087 | 25 | 0.423 | 45 | 0.707 | 65 | 0.906 | 85 | 0.996 |
| 6 | 0.105 | 26 | 0.438 | 46 | 0.719 | 66 | 0.914 | 86 | 0.998 |
| 7 | 0.122 | 27 | 0.454 | 47 | 0.731 | 67 | 0.921 | 87 | 0.999 |
| 8 | 0.139 | 28 | 0.469 | 48 | 0.743 | 68 | 0.927 | 88 | 0.999 |
| 9 | 0.156 | 29 | 0.485 | 49 | 0.755 | 69 | 0.934 | 89 | 1.000 |
| 10 | 0.174 | 30 | 0.500 | 50 | 0.766 | 70 | 0.940 | ||
| 11 | 0.191 | 31 | 0.515 | 51 | 0.777 | 71 | 0.946 | ||
| 12 | 0.208 | 32 | 0.530 | 52 | 0.788 | 72 | 0.951 | ||
| 13 | 0.225 | 33 | 0.545 | 53 | 0.799 | 73 | 0.956 | ||
| 14 | 0.242 | 34 | 0.559 | 54 | 0.809 | 74 | 0.961 | ||
| 15 | 0.259 | 35 | 0.574 | 55 | 0.819 | 75 | 0.966 | ||
| 16 | 0.276 | 36 | 0.588 | 56 | 0.829 | 76 | 0.970 | ||
| 17 | 0.292 | 37 | 0.602 | 57 | 0.839 | 77 | 0.974 | ||
| 18 | 0.309 | 38 | 0.616 | 58 | 0.848 | 78 | 0.978 | ||
| 19 | 0.326 | 39 | 0.629 | 59 | 0.857 | 79 | 0.982 | ||
| 20 | 0.342 | 40 | 0.643 | 60 | 0.866 | 80 | 0.985 |
練習問題
図の直角三角形について,印をつけた角(角度を\( \ \theta \ \)とする)に注目した場合の,斜辺・底辺・高さを答えましょう。
さらに,高さ:斜辺の比の値を求め,一覧表を利用して\( \ \theta \ \)がおおよそ何度か(何度から何度の間か)を求めましょう。
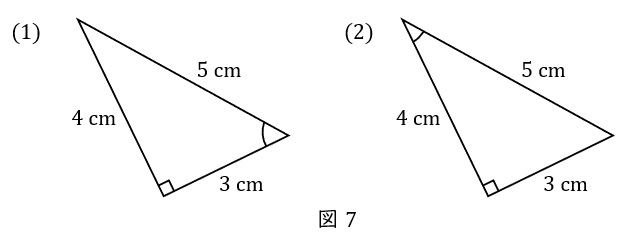
直角が右下,\( \ \theta \ \)が左下になるように直角三角形を置きます。そして,高さ:斜辺の比の値とは,高さ\( \ \div \ \)斜辺のことです。
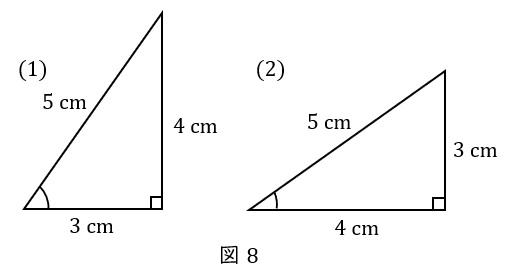
\( \ (1) \ \) 斜辺\( \ 5 \ \mathrm {cm} \ \),底辺\( \ 3 \ \mathrm {cm} \ \),高さ\( \ 4 \ \mathrm {cm} \ \),\( \ \theta \ \)は\( \ 53^\circ \ \)と\( \ 54^\circ \ \)の間
斜辺・底辺・高さは定義の通りです。
比の値は,高さ\( \ \div \ \)斜辺 \( \ = 4 \div 5 = 0.8 \ \)です。
一覧表から\( \ 0.8 \ \)に近い値を探して, \( \ \theta \ \)は\( \ 53^\circ \ \)と\( \ 54^\circ \ \)の間だと分かります。
\( \ (2) \ \) 斜辺\( \ 5 \ \mathrm {cm} \ \),底辺\( \ 4 \ \mathrm {cm} \ \),高さ\( \ 3 \ \mathrm {cm} \ \),\( \ \theta \ \)は\( \ 36^\circ \ \)と\( \ 37^\circ \ \)の間
斜辺・底辺・高さは定義の通りです。
比の値は,高さ\( \ \div \ \)斜辺 \( \ = 3 \div 5 = 0.6 \ \)です。
一覧表から\( \ 0.6 \ \)に近い値を探して,\( \ \theta \ \)は\( \ 36^\circ \ \)と\( \ 37^\circ \ \)の間だと分かります。
【別解】\( \ (1) \ \) の角度が\( \ 53^\circ \ \)と\( \ 54^\circ \ \)の間だと分かったので,\( \ 90^\circ \ \)からこれらの角度を引き算して,\( \ 36^\circ \ \)と\( \ 37^\circ \ \)の間である。


