Contents
- 1 高さ\( \ \div \ \)斜辺が\( \ \sin \theta \ \) (サイン)
- 2 \( \ \sin \theta \ \)は,”斜辺\( \ 1 \ \)の直角三角形の高さ” と考えよう
- 3 底辺\( \ \div \ \)斜辺が\( \ \cos \theta \ \) (コサイン)。 “斜辺\( \ 1 \ \)の直角三角形の底辺” と考えよう
- 4 \( \ \sin \theta \ \)と\( \ \cos \theta \ \)の覚え方
- 5 高さ\( \ \div \ \)底辺が\( \ \tan \theta \ \)(タンジェント)。”斜辺の傾き” と考えよう
- 6 練習問題
高さ\( \ \div \ \)斜辺が\( \ \sin \theta \ \) (サイン)
【三角比①】で述べた通り,直角三角形は\( \ \theta = 20^\circ \ \)なら,高さ\( \ \div \ \)斜辺\( \ = 0.342 \ \) です。
高さ\( \ \div \ \)斜辺 は,\( \ \sin \ \) (サイン)という記号を使って,このように書けます。
高さ\( \ \div \ \)斜辺\( \ =\sin \theta \ \)
\( \ \theta = 20^\circ \ \)なら,こうなります。
\[
\begin{eqnarray}
\sin 20^\circ &=&0.342 \\[ 5pt ]
\end{eqnarray}
\]
\( \ \sin 20^\circ \ \)は「サイン\( \ 20 \ \)ど」と読み,”三角形の高さを斜辺で割った値” という意味です。
どんな三角形かというと,\( \ \theta = 20^\circ \ \)の直角三角形です。
この\( \ \sin \ \) という記号がとっつきにくいので,もう少し説明します。
例えば,\( \ \sqrt{2} \ \)ってありますよね。”\( \ 2 \ \)乗して\( \ 2 \ \)になる数” です。
実際の数字は\( \ 1.414\cdots \ \)ですが,実際の数値よりも,\( \ 2 \ \)乗して\( \ 2 \ \)になることが重要なので,屋根のような記号を使って\( \ \sqrt{2} \ \)と書くのです。
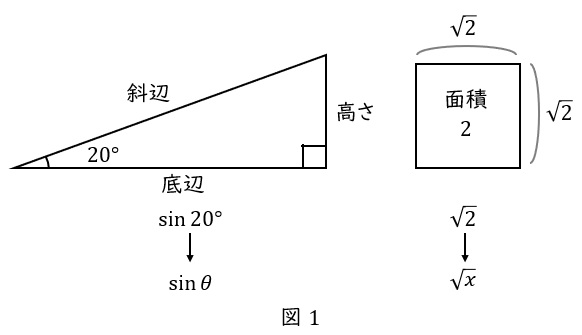
\( \ \sin \ \) も同じです。”直角三角形の高さを斜辺で割った値” という意味の記号です。
\( \ \sin \ \) の直後が具体的な角度であれば,具体的な数値が存在します。
\[
\begin{eqnarray}
\sin 20^\circ &=&0.342 \\[ 5pt ]
\end{eqnarray}
\]
具体的な角度がなく,一般化して書く場合は,角度を\( \ \theta \ \)として,
\[
\begin{eqnarray}
\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
と書きます。
これは,”\( \ 2 \ \)乗して\( \ x \ \)になる数” のことを\( \ \sqrt{x} \ \)と書くのと同じです。
まとめると,”\( \ \sin \theta \ \) とは直角三角形の高さを斜辺で割った値” という意味です。
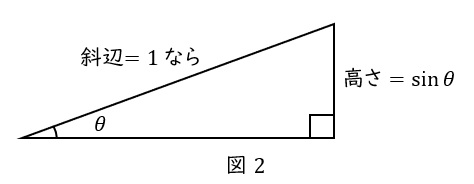
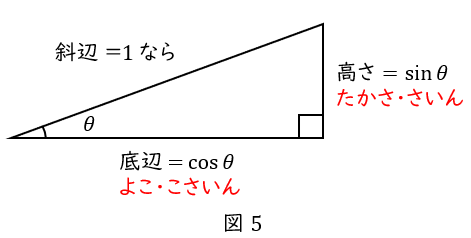
\( \ \sin \theta \ \)は,”斜辺\( \ 1 \ \)の直角三角形の高さ” と考えよう
高さ\( \ \div \ \)斜辺,という割り算の形は覚えにくいですね。
そこで,三角形を拡大または縮小コピーして,斜辺を\( \ 1 \ \)にします。そうすれば,高さがそのまま\( \ \sin \theta \ \)となります。
要するに,”\( \ \sin \theta \ \)とは,直角三角形を拡大・縮小して,斜辺を\( \ 1 \ \)にしたときの高さ” です。
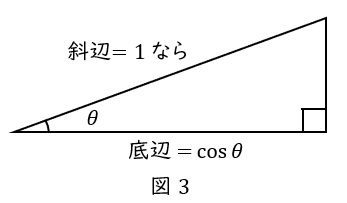
底辺\( \ \div \ \)斜辺が\( \ \cos \theta \ \) (コサイン)。 “斜辺\( \ 1 \ \)の直角三角形の底辺” と考えよう
\( \ \sin \theta \ \)は高さを斜辺で割った値でしたが,
高さではなく,底辺を斜辺で割った値が,\( \ \cos \theta \ \)(コサイン)です。
底辺\( \ \div \ \)斜辺\( \ =\cos \theta \ \)
これも,斜辺\( \ 1 \ \)の直角三角形で考えましょう。
三角形を拡大または縮小して,斜辺を\( \ 1 \ \)にします。そうすれば,底辺がそのまま\( \ \cos \theta \ \)となります。
要するに,”\( \ \cos \theta \ \)とは,直角三角形を拡大・縮小して,斜辺を\( \ 1 \ \)にしたときの底辺” です。
\( \ \sin \theta \ \)と\( \ \cos \theta \ \)の覚え方
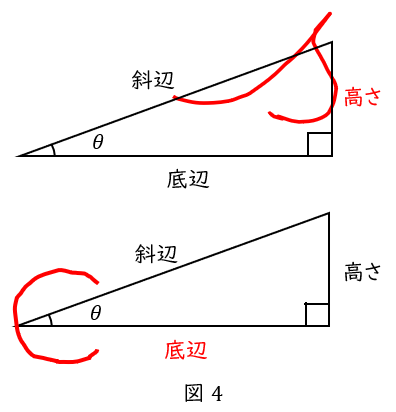
下図の通りアルファベットの\( \ s,c \ \)の筆記体を使った覚え方が一般的です。
\( \ \sin \theta \ \)は\( \ s \ \)の書き順に従って,”斜辺” 分の “高さ” ,
\( \ \cos \theta \ \)は\( \ c \ \)の書き順に従って,”斜辺” 分の “底辺” というわけです。
しかし筆記体は,\( \ 2002 \ \)年に中学校の学習指導要領から外れたので,習ってない方も多いでしょう。
そこで,日本語を使った覚え方を紹介します。
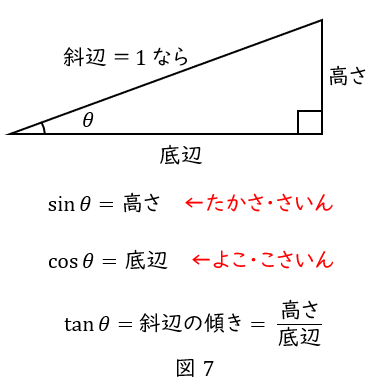
\( \ \sin \theta \ \)は,斜辺が\( \ 1 \ \)のときの高さですから,”たかさ,さいん” です。
\( \ \cos \theta \ \)は,斜辺が\( \ 1 \ \)のときの底辺,つまり横線ですから,”よこ,こさいん” です。
高さ\( \ \div \ \)底辺が\( \ \tan \theta \ \)(タンジェント)。”斜辺の傾き” と考えよう
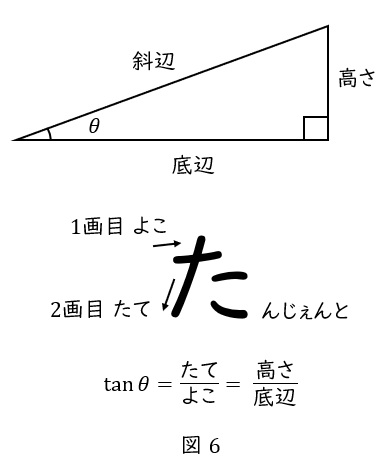
最後に\( \ \tan \theta \ \)(タンジェント)を紹介します。高さを底辺で割った値のことです。
高さ\( \ \div \ \)底辺\( \ =\tan \theta \ \)
覚え方は,ひらがなの「た」を書くとき,一画目が横線,二画目が縦線ですよね。
したがって,「よこ(底辺)」 分の 「たて(高さ)」が\( \ \tan \theta \ \)です。
さて,\( \ \tan \theta \ \)が,高さ\( \ \div \ \)底辺ということは, \( \ \sin \theta,\cos \theta,\tan \theta \ \)には以下の関係が成り立ちます。
\[
\begin{eqnarray}
\tan \theta =\displaystyle \frac{高さ}{底辺} =\displaystyle \frac{\displaystyle \frac{高さ}{斜辺}}{\displaystyle \frac{底辺}{斜辺}} = \displaystyle \frac{\sin \theta}{\cos \theta} \\[ 5pt ]
\end{eqnarray}
\]
上式の左辺と右辺より,
\[
\begin{eqnarray}
\tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta} \\[ 5pt ]
\end{eqnarray}
\]
直角三角形では,\( \ \tan \theta \ \)は斜辺の傾きとなります。
練習問題
印をつけた角(角度を\( \ \theta \ \)とする)に注目した場合の,\( \ \sin \theta,\cos \theta,\tan \theta \ \)を求めましょう。
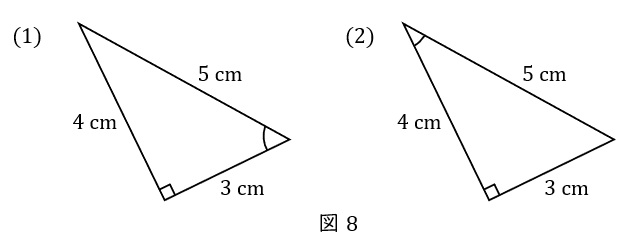
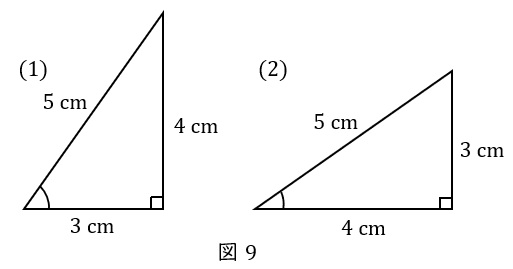
\( \ (1) \ \) \( \ \sin \theta = 0.8 \ \),\( \ \cos \theta = 0.6 \ \),\( \ \tan \theta = 1.333\cdots \ \)
まずは直角が右下,\( \ \theta \ \)が左下になるように置き,斜辺・底辺・高さを確認しましょう。
斜辺\( \ 5 \ \mathrm {cm} \ \),底辺\( \ 3 \ \mathrm {cm} \ \),高さ\( \ 4 \ \mathrm {cm} \ \)なので,
\[
\begin{eqnarray}
\sin \theta = \displaystyle \frac{高さ}{斜辺} = \displaystyle \frac{4}{5} = 0.8 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\cos \theta = \displaystyle \frac{底辺}{斜辺} = \displaystyle \frac{3}{5} = 0.6 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\tan \theta = \displaystyle \frac{高さ}{底辺} = \displaystyle \frac{4}{3} = 1.333\cdots \\[ 5pt ]
\end{eqnarray}
\]
\( \ (2) \ \) \( \ \sin \theta = 0.6 \ \),\( \ \cos \theta = 0.8 \ \),\( \ \tan \theta = 0.75 \ \)
まずは直角が右下,\( \ \theta \ \)が左下になるように置き,斜辺・底辺・高さを確認しましょう。
斜辺\( \ 5 \ \mathrm {cm} \ \),底辺\( \ 4 \ \mathrm {cm} \ \),高さ\( \ 3 \ \mathrm {cm} \ \)なので,
\[
\begin{eqnarray}
\sin \theta = \displaystyle \frac{高さ}{斜辺} = \displaystyle \frac{3}{5} = 0.6 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\cos \theta = \displaystyle \frac{底辺}{斜辺} = \displaystyle \frac{4}{5} = 0.8 \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\tan \theta = \displaystyle \frac{高さ}{底辺} = \displaystyle \frac{3}{4} = 0.75 \\[ 5pt ]
\end{eqnarray}
\]


