Contents
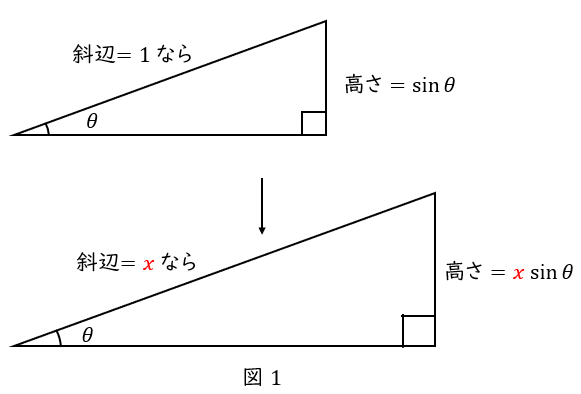
【\( \ \sin \theta \ \)の使い方】高さ\( \ = \ \)斜辺の長さ\( \ \times \sin \theta\ \)
【三角比①】で,\( \ \theta = 20^\circ \ \)かつ斜辺\( \ 2 \ \mathrm {cm} \ \)の直角三角形を描いてもらいました。このとき,”\( \ \theta \ \)と斜辺が決まっていれば,高さは自動的に決まった” と実感できたと思います。これについて解説します。
\( \ \theta \ \)が決まれば,\( \ \sin \theta \ \)の値は自動的に決まりますから,\( \ \sin \theta \ \)は一覧表にできます。
| 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.017 | 21 | 0.358 | 41 | 0.656 | 61 | 0.875 | 81 | 0.988 |
| 2 | 0.035 | 22 | 0.375 | 42 | 0.669 | 62 | 0.883 | 82 | 0.990 |
| 3 | 0.052 | 23 | 0.391 | 43 | 0.682 | 63 | 0.891 | 83 | 0.993 |
| 4 | 0.070 | 24 | 0.407 | 44 | 0.695 | 64 | 0.899 | 84 | 0.995 |
| 5 | 0.087 | 25 | 0.423 | 45 | 0.707 | 65 | 0.906 | 85 | 0.996 |
| 6 | 0.105 | 26 | 0.438 | 46 | 0.719 | 66 | 0.914 | 86 | 0.998 |
| 7 | 0.122 | 27 | 0.454 | 47 | 0.731 | 67 | 0.921 | 87 | 0.999 |
| 8 | 0.139 | 28 | 0.469 | 48 | 0.743 | 68 | 0.927 | 88 | 0.999 |
| 9 | 0.156 | 29 | 0.485 | 49 | 0.755 | 69 | 0.934 | 89 | 1.000 |
| 10 | 0.174 | 30 | 0.500 | 50 | 0.766 | 70 | 0.940 | ||
| 11 | 0.191 | 31 | 0.515 | 51 | 0.777 | 71 | 0.946 | ||
| 12 | 0.208 | 32 | 0.530 | 52 | 0.788 | 72 | 0.951 | ||
| 13 | 0.225 | 33 | 0.545 | 53 | 0.799 | 73 | 0.956 | ||
| 14 | 0.242 | 34 | 0.559 | 54 | 0.809 | 74 | 0.961 | ||
| 15 | 0.259 | 35 | 0.574 | 55 | 0.819 | 75 | 0.966 | ||
| 16 | 0.276 | 36 | 0.588 | 56 | 0.829 | 76 | 0.970 | ||
| 17 | 0.292 | 37 | 0.602 | 57 | 0.839 | 77 | 0.974 | ||
| 18 | 0.309 | 38 | 0.616 | 58 | 0.848 | 78 | 0.978 | ||
| 19 | 0.326 | 39 | 0.629 | 59 | 0.857 | 79 | 0.982 | ||
| 20 | 0.342 | 40 | 0.643 | 60 | 0.866 | 80 | 0.985 |
例えば\( \ \theta = 20^\circ \ \)なら,一覧表より\( \ \sin 20^\circ = 0.342 \ \)です。
\( \ \sin \ \)とは ”斜辺\( \ 1 \ \)のときの高さ” ですから,”斜辺が\( \ 1 \ \)なら高さは\( \ 0.342 \ \)” ということです。
実際の斜辺が\( \ 2 \ \mathrm {cm} \ \)なら,高さは\( \ 2 \times 0.342 = 0.684 \ \mathrm {[cm]} \ \)となります。
一般化すると,
高さ\( \ = \ \)斜辺\( \ \times \sin \theta \ \)
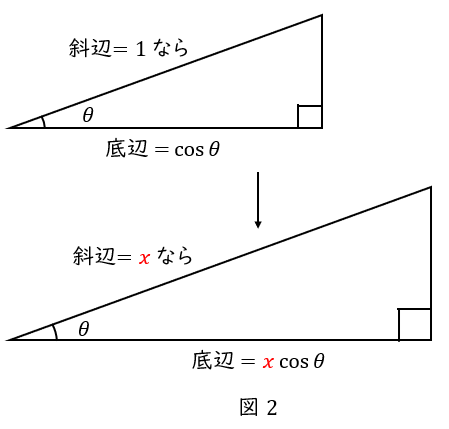
【\( \ \cos \theta \ \)の使い方】底辺\( \ = \ \)斜辺の長さ\( \ \times \cos \theta \ \)
高さではなく底辺を求めたい場合は,\( \ \cos \ \)を使います。
\( \ \theta \ \)が決まれば,\( \ \cos \theta \ \)の値は自動的に決まりますから,\( \ \cos \theta \ \)も一覧表にできます。
| 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 | 角度[°] | 高さ/斜辺 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.000 | 21 | 0.934 | 41 | 0.755 | 61 | 0.485 | 81 | 0.156 |
| 2 | 0.999 | 22 | 0.927 | 42 | 0.743 | 62 | 0.469 | 82 | 0.139 |
| 3 | 0.999 | 23 | 0.921 | 43 | 0.731 | 63 | 0.454 | 83 | 0.122 |
| 4 | 0.998 | 24 | 0.914 | 44 | 0.719 | 64 | 0.438 | 84 | 0.105 |
| 5 | 0.996 | 25 | 0.906 | 45 | 0.707 | 65 | 0.423 | 85 | 0.087 |
| 6 | 0.995 | 26 | 0.899 | 46 | 0.695 | 66 | 0.407 | 86 | 0.070 |
| 7 | 0.993 | 27 | 0.891 | 47 | 0.682 | 67 | 0.391 | 87 | 0.052 |
| 8 | 0.990 | 28 | 0.883 | 48 | 0.669 | 68 | 0.375 | 88 | 0.035 |
| 9 | 0.988 | 29 | 0.875 | 49 | 0.656 | 69 | 0.358 | 89 | 0.017 |
| 10 | 0.985 | 30 | 0.866 | 50 | 0.643 | 70 | 0.342 | ||
| 11 | 0.982 | 31 | 0.857 | 51 | 0.629 | 71 | 0.326 | ||
| 12 | 0.978 | 32 | 0.848 | 52 | 0.616 | 72 | 0.309 | ||
| 13 | 0.974 | 33 | 0.839 | 53 | 0.602 | 73 | 0.292 | ||
| 14 | 0.970 | 34 | 0.829 | 54 | 0.588 | 74 | 0.276 | ||
| 15 | 0.966 | 35 | 0.819 | 55 | 0.574 | 75 | 0.259 | ||
| 16 | 0.961 | 36 | 0.809 | 56 | 0.559 | 76 | 0.242 | ||
| 17 | 0.956 | 37 | 0.799 | 57 | 0.545 | 77 | 0.225 | ||
| 18 | 0.951 | 38 | 0.788 | 58 | 0.530 | 78 | 0.208 | ||
| 19 | 0.946 | 39 | 0.777 | 59 | 0.515 | 79 | 0.191 | ||
| 20 | 0.940 | 40 | 0.766 | 60 | 0.500 | 80 | 0.174 |
例えば\( \ \theta = 20^\circ \ \)なら,一覧表より\( \ \cos 20^\circ = 0.940 \ \)です。
\( \ \cos \ \)とは ”斜辺\( \ 1 \ \)のときの底辺” ですから,”斜辺が\( \ 1 \ \)なら底辺は\( \ 0.940 \ \)” ということです。
実際の斜辺が\( \ 2 \ \mathrm {cm} \ \)なら,底辺は\( \ 2 \times 0.940 = 1.88 \ \mathrm {[cm]} \ \)となります。
一般化すると,
底辺\( \ = \ \)斜辺\( \ \times \cos \theta \ \)
練習問題
\( \ \sin \theta \ \)と\( \ \cos \theta \ \)の一覧表を用いて,次の値を求めましょう。
\( \ (1) \ \) 斜辺\( \ 5 \ \mathrm {cm} \ \),\( \ \theta = 25^\circ \ \)の直角三角形の高さ
\( \ (2) \ \) 斜辺\( \ 12 \ \mathrm {cm} \ \),\( \ \theta = 32^\circ \ \)の直角三角形の高さ
\( \ (3) \ \) 斜辺\( \ 4 \ \mathrm {cm} \ \),\( \ \theta = 15^\circ \ \)の直角三角形の底辺
\( \ (4) \ \) 斜辺\( \ 9 \ \mathrm {cm} \ \),\( \ \theta = 40^\circ \ \)の直角三角形の底辺
\( \ (5) \ \) 斜辺\( \ 3 \ \mathrm {cm} \ \),\( \ \theta = 28^\circ \ \)の直角三角形の高さと底辺を求めたうえで,\( \ \tan 28^\circ \ \)
\( \ (6) \ \) 斜辺\( \ 6 \ \mathrm {cm} \ \),\( \ \theta = 70^\circ \ \)の直角三角形の高さと底辺を求めたうえで,\( \ \tan 70^\circ \ \)
\( \ (1) \ \) \( \ 2.115 \ \mathrm {cm} \ \)
高さ\( \ = \ \)斜辺\( \ \times \sin \theta \ \)より,
\[
\begin{eqnarray}
5 \times \sin 25^\circ = 5 \times 0.423 = 2.115 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (2) \ \) \( \ 6.36 \ \mathrm {cm} \ \)
高さ\( \ = \ \)斜辺\( \ \times \sin \theta \ \)より,
\[
\begin{eqnarray}
12 \times \sin 32^\circ = 12 \times 0.530 = 6.36 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (3) \ \) \( \ 3.864 \ \mathrm {cm} \ \)
底辺\( \ = \ \)斜辺\( \ \times \cos \theta \ \)より,
\[
\begin{eqnarray}
4 \times \cos 15^\circ = 4 \times 0.966 = 3.864 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (4) \ \) \( \ 6.894 \ \mathrm {cm} \ \)
底辺\( \ = \ \)斜辺\( \ \times \cos \theta \ \)より,
\[
\begin{eqnarray}
9 \times \cos 40^\circ = 9 \times 0.766 = 6.894 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (5) \ \) 高さ\( \ 1.407 \ \),底辺\( \ 2.649 \ \),\( \ \tan 28^\circ ≒ 0.531 \ \)
\( \ \tan \theta = \ \)高さ\( \ \div \ \)底辺 なので,まずは高さと底辺を求めます。
高さ\( \ = \ \)斜辺\( \ \times \sin \theta \ \)より,
\[
\begin{eqnarray}
3 \times \sin 28^\circ = 3 \times 0.469 = 1.407 \\[ 5pt ]
\end{eqnarray}
\]
底辺\( \ = \ \)斜辺\( \ \times \cos \theta \ \)より,
\[
\begin{eqnarray}
3 \times \cos 28^\circ = 3 \times 0.883 = 2.649 \\[ 5pt ]
\end{eqnarray}
\]
\( \ \tan \theta = \ \)高さ\( \ \div \ \)底辺 より,
\[
\begin{eqnarray}
\tan 28^\circ = 1.407 \div 2.649 ≒0.531 \\[ 5pt ]
\end{eqnarray}
\]
【別解】\( \ \tan 28^\circ \ \)はこのように求めることもできます。
\( \ \tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta} \ \)より,
\[
\begin{eqnarray}
\tan 28^\circ = \displaystyle \frac{\sin 28^\circ}{\cos 28^\circ} = \displaystyle \frac{0.469}{0.883}≒0.531 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (6) \ \) 高さ\( \ 5.64 \ \),底辺\( \ 2.052 \ \),\( \ \tan 70^\circ ≒ 2.749 \ \)
\( \ \tan \theta = \ \)高さ\( \ \div \ \)底辺 なので,まずは高さと底辺を求めます。
高さ\( \ = \ \)斜辺\( \ \times \sin \theta \ \)より,
\[
\begin{eqnarray}
6 \times \sin 70^\circ = 6 \times 0.940 = 5.64 \\[ 5pt ]
\end{eqnarray}
\]
底辺\( \ = \ \)斜辺\( \ \times \cos \theta \ \)より,
\[
\begin{eqnarray}
6 \times \cos 70^\circ = 6 \times 0.342 = 2.052 \\[ 5pt ]
\end{eqnarray}
\]
\( \ \tan \theta = \ \)高さ\( \ \div \ \)底辺 より,
\[
\begin{eqnarray}
\tan 70^\circ = 5.64 \div 2.052 ≒ 2.749 \\[ 5pt ]
\end{eqnarray}
\]
【別解】\( \ \tan 70^\circ \ \)はこのように求めることもできます。
\( \ \tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta} \ \)より,
\[
\begin{eqnarray}
\tan 70^\circ = \displaystyle \frac{\sin 70^\circ}{\cos 70^\circ} = \displaystyle \frac{0.940}{0.342} ≒2.749 \\[ 5pt ]
\end{eqnarray}
\]


