Contents
- 1 三角定規は,特別な直角三角形
- 2 \( \ 45^\circ \ \)と\( \ 45^\circ \ \)の直角三角形は,正方形の半分
- 3 \( \ 30^\circ \ \)と\( \ 60^\circ \ \)の直角三角形は,正三角形の半分
- 4 角度を忘れたときの思い出し方
- 5 辺の長さの比を忘れたときの思い出し方
- 6 \( \ \sin 30^\circ \ \)はいくつ?
- 7 \( \ \cos 45^\circ \ \)はいくつ?
- 8 \( \ \tan \theta \ \)はいくつ?
- 9 練習問題
- 10 特別な直角三角形における\( \ \sin \ \),\( \ \cos \ \)の覚え方
- 11 特別角(\( \ 30^\circ \ \),\( \ 45^\circ \ \),\( \ 60^\circ \ \),)の三角比(\( \ \sin \ \),\( \ \cos \ \))
三角定規は,特別な直角三角形
小学生の時に,三角定規を使っていましたよね。この\( \ 2 \ \)種類でした。
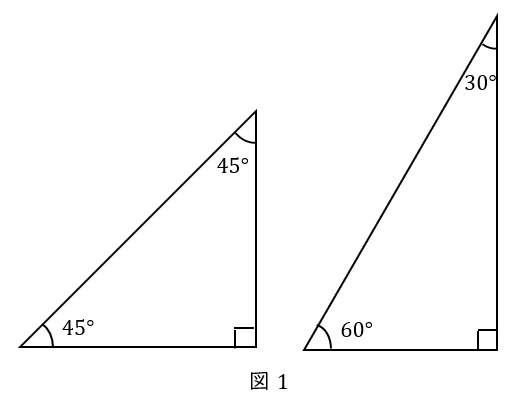
角度は上図の通り,二等辺三角形の方は\( \ 45^\circ \ \)と\( \ 45^\circ \ \)と\( \ 90^\circ \ \),もう一つは\( \ 30^\circ \ \)と\( \ 60^\circ \ \)と\( \ 90^\circ \ \)です。
これは特別な直角三角形で,辺の長さの比がこうなります。
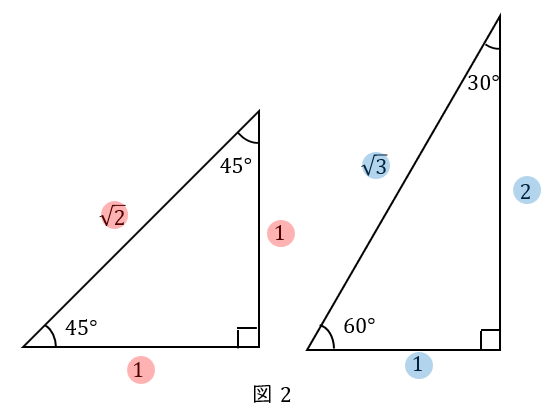
この角度と比の覚え方を解説します。
\( \ 45^\circ \ \)と\( \ 45^\circ \ \)の直角三角形は,正方形の半分
一辺の長さが\( \ 1 \ \)の正方形を,斜めに切って半分にします。食パンを切って三角サンドイッチを作るイメージです。
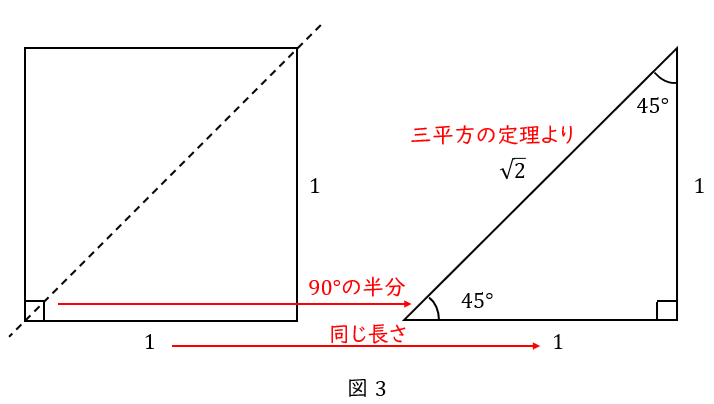
\( \ 90^\circ \ \)の半分ですから,角度は\( \ 45^\circ \ \)ですね。
底辺と高さは,正方形の一辺の長さと同じ,\( \ 1 \ \)です。
斜辺の長さは,三平方の定理より,
\[
\begin{eqnarray}
\sqrt{1^2+1^2} = \sqrt{1+1} = \sqrt{2} \\[ 5pt ]
\end{eqnarray}
\]
したがって,辺の比は \( \ 1:1:\sqrt{2} \ \)です。
\( \ 30^\circ \ \)と\( \ 60^\circ \ \)の直角三角形は,正三角形の半分
今度は一辺の長さが\( \ 1 \ \)の正三角形を,縦に半分にします。おにぎりを半分にするイメージです。
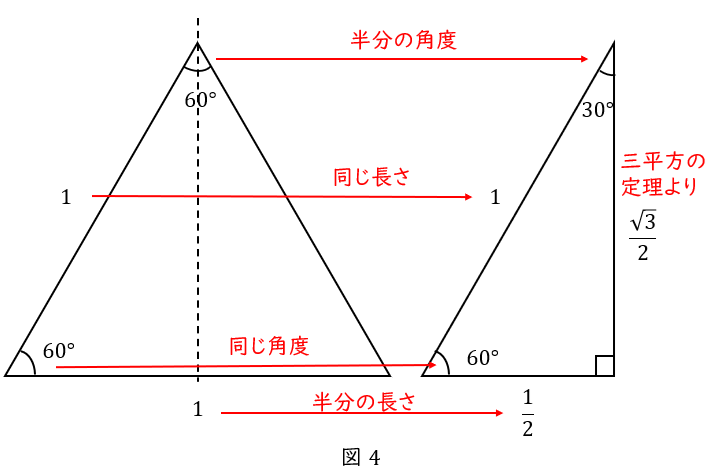
直角以外の角のうち,大きい角は正三角形と同じ\( \ 60^\circ \ \),もう一つの角は,\( \ 60^\circ \ \)の半分の\( \ 30^\circ \ \)です。
斜辺は,正三角形の一辺の長さと同じ\( \ 1 \ \)です。
底辺は,その半分の\( \ \displaystyle \frac{1}{2} \ \)です。
高さは,三平方の定理より
\[
\begin{eqnarray}
\sqrt{1^2-\left(\displaystyle \frac{1}{2} \right) ^2}
= \sqrt{1-\displaystyle \frac{1}{4} }
= \sqrt{\displaystyle \frac{3}{4}}
= \displaystyle \frac{\sqrt{3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
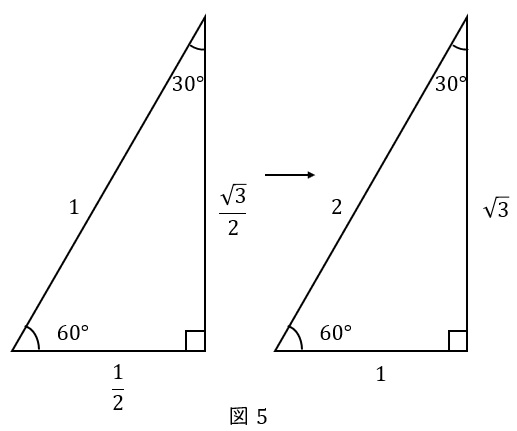
したがって,辺の比は \( \ \displaystyle \frac{1}{2}:1:\displaystyle \frac{\sqrt{3}}{2} \ \)です。
このままでもいいのですが,分数をなくすために\( \ 2 \ \)倍すると,\( \ 1:2:\sqrt{3} \ \)です。
角度を忘れたときの思い出し方
”三角定規” を思い出しましょう。
一つは二等辺三角形ですから簡単です。\( \ 90^\circ \ \)の半分の,\( \ 45^\circ \ \)と\( \ 45^\circ \ \)です。
問題はもう一つの三角定規です。
\( \ 10^\circ \ \)や\( \ 20^\circ \ \)だとかなり鋭いので,小学生に持たせるのは危険です。友達を突っついてケガをさせるでしょう。
\( \ 40^\circ \ \)だと,\( \ 45^\circ \ \)と近すぎます。
ということは\( \ 30^\circ \ \)です。
一方の角度が\( \ 30^\circ \ \)なら,もう一方は\( \ 90-30=60 \ \)ですから,\( \ 60^\circ \ \)です。
以上より,\( \ 30^\circ \ \)と\( \ 60^\circ \ \)です。
辺の長さの比を忘れたときの思い出し方
ノートに\( \ 1,2,3,4 \ \)と書いて,すべてにルートをつけましょう。
\[
\begin{eqnarray}
\sqrt{1},\sqrt{2},\sqrt{3},\sqrt{4} \\[ 5pt ]
\end{eqnarray}
\]
ここで,\( \ \sqrt{1} =1 \ \),\( \ \sqrt{4} =2 \ \)ですから,こうなります。
\[
\begin{eqnarray}
1,\sqrt{2},\sqrt{3},2 \\[ 5pt ]
\end{eqnarray}
\]
今,この\( \ 4 \ \)つの数字は大きさ順に並んでいます。
問題は,これらの数字がどの三角形のどの辺に対応するかです。
まず\( \ 2 \ \)つの三角形を重ねます。
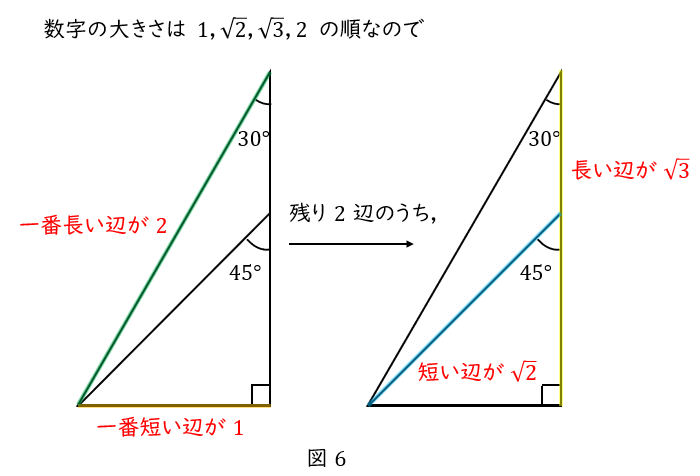
一番短い辺が,一番小さい数字である\( \ 1 \ \)ですね。
一番長い辺が,一番大きい数字である\( \ 2 \ \)です。
あとは,\( \ 2 \ \)つの斜辺のうち,短い方が\( \ \sqrt{2} \ \),長い方が\( \ \sqrt{3} \ \)です。
\( \ \sin 30^\circ \ \)はいくつ?
ここまでを踏まえて,\( \ \sin 30^\circ \ \)がいくつかを考えてみましょう。
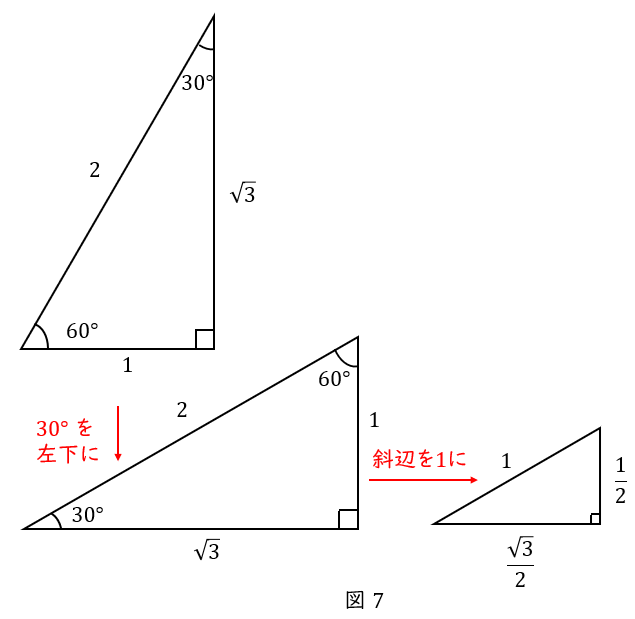
まずは\( \ \theta = 30^\circ \ \)の直角三角形を描きます。
\( \ \theta = 30^\circ \ \)は特別な直角三角形で,辺の比が\( \ 1:2:\sqrt{3} \ \)です。
\( \ \sin \ \)とは,斜辺\( \ 1 \ \)の三角形の高さでしたね。覚え方は「たかさ,さいん」です。
斜辺が\( \ 1 \ \)になるように縮小すると,高さは\( \ \displaystyle \frac{1}{2} \ \)になるので,
\[
\begin{eqnarray}
\sin 30^\circ = \displaystyle \frac{1}{2} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \cos 45^\circ \ \)はいくつ?
続いて,\( \ \cos 45^\circ \ \)も求めましょう。
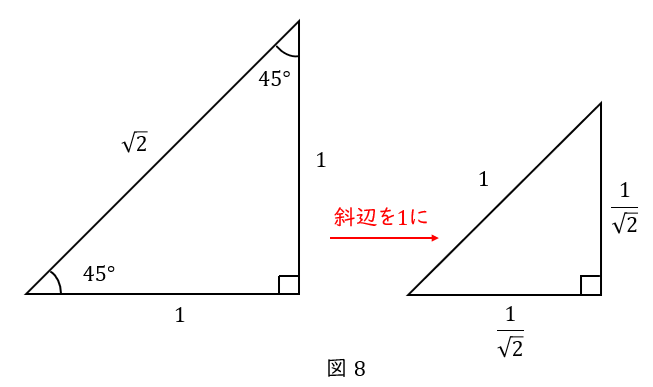
まずは\( \ \theta = 45^\circ \ \)の直角三角形を描きます。
\( \ \theta = 45^\circ \ \)は特別な直角三角形で,辺の比が\( \ 1:1:\sqrt{2} \ \)です。
\( \ \cos \ \)とは,斜辺\( \ 1 \ \)の三角形の底辺でしたね。覚え方は「よこ,こさいん」です。
斜辺が\( \ 1 \ \)になるように縮小すると,底辺は\( \ \displaystyle \frac{1}{\sqrt{2}} \ \)なので,
\[
\begin{eqnarray}
\cos 45^\circ = \displaystyle \frac{1}{\sqrt{2}} \\[ 5pt ]
\end{eqnarray}
\]
または\( \ \displaystyle \frac{\sqrt{2}}{2} \ \)も正解です。
\( \ \tan \theta \ \)はいくつ?
\( \ \tan \theta \ \)は,\( \ \sin \theta \ \)と\( \ \cos \theta \ \)を使って計算することができましたね。
覚えている方は,このまま練習問題に進んでください。
忘れてしまった方は,【三角比②】でご確認ください。
練習問題
表の空欄を埋めましょう。
| \( \ 30^\circ \ \) | \( \ 45^\circ \ \) | \( \ 60^\circ \ \) | |
|---|---|---|---|
| \( \ \sin \theta \ \) | \( \ \displaystyle \frac{1}{2} \ \) | \( \ ( 1 ) \ \) | \( \ ( 2 ) \ \) |
| \( \ \cos \theta \ \) | \( \ ( 3 ) \ \) | \( \ \displaystyle \frac{1}{\sqrt{2}} \ \) | \( \ ( 4 ) \ \) |
| \( \ \tan \theta \ \) | \( \ ( 5 ) \ \) | \( \ ( 6 ) \ \) | \( \ ( 7 ) \ \) |
| \( \ 30^\circ \ \) | \( \ 45^\circ \ \) | \( \ 60^\circ \ \) | |
|---|---|---|---|
| \( \ \sin \theta \ \) | \( \ \displaystyle \frac{1}{2} \ \) | \( \ \displaystyle \frac{1}{\sqrt{2}} \ \)または\( \ \displaystyle \frac{\sqrt{2}}{2} \ \) | \( \ \displaystyle \frac{\sqrt{3}}{2} \ \) |
| \( \ \cos \theta \ \) | \( \ \displaystyle \frac{\sqrt{3}}{2} \ \) | \( \ \displaystyle \frac{1}{\sqrt{2}} \ \)または\( \ \displaystyle \frac{\sqrt{2}}{2} \ \) | \( \ \displaystyle \frac{1}{2} \ \) |
| \( \ \tan \theta \ \) | \( \ \displaystyle \frac{1}{\sqrt{3}} \ \)または\( \ \displaystyle \frac{\sqrt{3}}{3} \ \) | \( \ 1 \ \) | \( \ \sqrt{3} \ \) |
\( \ (1) \ \) \( \ \sin 45^\circ = \displaystyle \frac{1}{\sqrt{2}} \ \)
まずは\( \ \theta = 45^\circ \ \)の直角三角形を描きます。
\( \ \theta = 45^\circ \ \)は特別な直角三角形で,辺の比が\( \ 1:1:\sqrt{2} \ \)です。
\( \ \sin \ \)とは,斜辺\( \ 1 \ \)の三角形の ”高さ” でしたね。覚え方は「たかさ,さいん」です。
斜辺を\( \ 1 \ \)にすると,高さは\( \ \displaystyle \frac{1}{\sqrt{2}} \ \)なので,
\[
\begin{eqnarray}
\sin 45^\circ = \displaystyle \frac{1}{\sqrt{2}} \\[ 5pt ]
\end{eqnarray}
\]
または\( \ \displaystyle \frac{\sqrt{2}}{2} \ \)も正解です。
下図は図\( \ 8 \ \)と同じです。

\( \ (2) \ \) \( \ \cos 30^\circ = \displaystyle \frac{\sqrt{3}}{2} \ \)
まずは\( \ \theta = 30^\circ \ \)の直角三角形を描きます。
\( \ \theta = 30^\circ \ \)は特別な直角三角形で,辺の比が\( \ 1:2:\sqrt{3} \ \)です。
\( \ \cos \ \)とは,斜辺\( \ 1 \ \)の三角形の ”底辺” でしたね。覚え方は「よこ,こさいん」です。
斜辺を\( \ 1 \ \)にすると,底辺は\( \ \displaystyle \frac{\sqrt{3}}{2} \ \)なので,
\[
\begin{eqnarray}
\cos 30^\circ = \displaystyle \frac{\sqrt{3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
下図は図\( \ 7 \ \)と同じです。

\( \ (3) \ \) \( \ \sin 60^\circ = \displaystyle \frac{\sqrt{3}}{2} \ \)
まずは\( \ \theta = 60^\circ \ \)の直角三角形を描きます。
\( \ \theta = 60^\circ \ \)は特別な直角三角形で,辺の比が\( \ 1:2:\sqrt{3} \ \)です。
\( \ \sin \ \)とは,斜辺\( \ 1 \ \)の三角形の ”高さ” でしたね。覚え方は「たかさ,さいん」です。
斜辺を\( \ 1 \ \)にすると,高さは\( \ \displaystyle \frac{\sqrt{3}}{2} \ \)なので,
\[
\begin{eqnarray}
\sin 60^\circ = \displaystyle \frac{\sqrt{3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
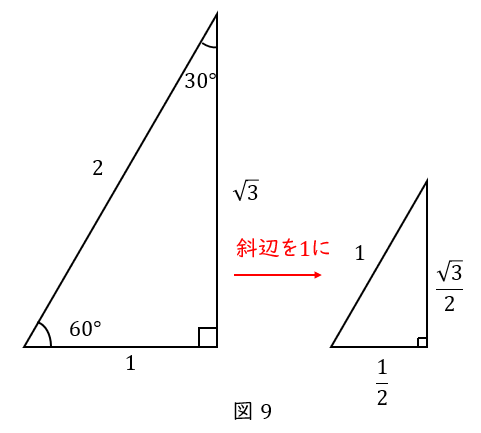
\( \ (4) \ \) \( \ \cos 60^\circ = \displaystyle \frac{1}{2} \ \)
まずは\( \ \theta = 60^\circ \ \)の直角三角形を描きます。
\( \ \theta = 60^\circ \ \)は特別な直角三角形で,辺の比が\( \ 1:2:\sqrt{3} \ \)です。
\( \ \cos \ \)とは,斜辺\( \ 1 \ \)の三角形の ”底辺” でしたね。覚え方は「よこ,こさいん」です。
斜辺を\( \ 1 \ \)にすると,底辺は\( \ \displaystyle \frac{1}{2} \ \)なので,
\[
\begin{eqnarray}
\cos 60^\circ = \displaystyle \frac{1}{2} \\[ 5pt ]
\end{eqnarray}
\]
下図は図\( \ 9 \ \)と同じです。

\( \ (5) \ \) \( \ \tan 30^\circ = \displaystyle \frac{1}{\sqrt{3}} \ \)
\( \ \tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta} \ \)ですから,
\[
\begin{eqnarray}
\tan 30^\circ = \displaystyle \frac{\sin 30^\circ}{\cos 30^\circ}
=\displaystyle \frac{\displaystyle \frac{1}{2}}{\displaystyle \frac{\sqrt{3}}{2}}
=\displaystyle \frac{1}{\sqrt{3}} \\[ 5pt ]
\end{eqnarray}
\]
または\( \ \displaystyle \frac{\sqrt{3}}{3} \ \)も正解です。
\( \ (6) \ \) \( \ \tan 45^\circ = 1 \ \)
\( \ \tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta} \ \)ですから,
\[
\begin{eqnarray}
\tan 45^\circ = \displaystyle \frac{\sin 45^\circ}{\cos 45^\circ}
= \displaystyle \frac{\displaystyle \frac{1}{\sqrt{2}}}{\sqrt{2}}
= 1 \\[ 5pt ]
\end{eqnarray}
\]
\( \ (7) \ \) \( \ \tan 60^\circ = \sqrt{3} \ \)
\( \ \tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta} \ \)ですから,
\[
\begin{eqnarray}
\tan 60^\circ = \displaystyle \frac{\sin 60^\circ}{\cos 60^\circ}
=\displaystyle \frac{\displaystyle \frac{\sqrt{3}}{2}}{\displaystyle \frac{1}{2}}
=\sqrt{3} \\[ 5pt ]
\end{eqnarray}
\]
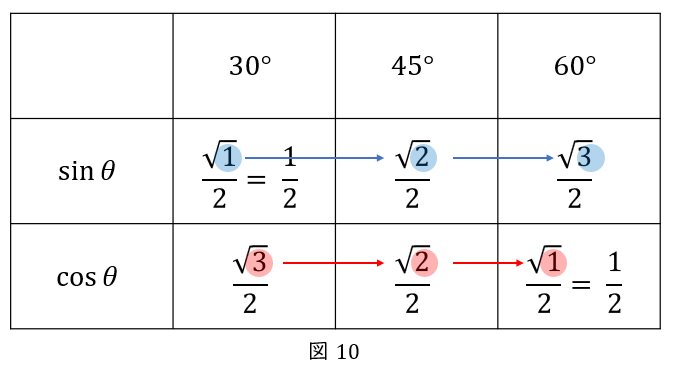
特別な直角三角形における\( \ \sin \ \),\( \ \cos \ \)の覚え方
すべて\( \ \displaystyle \frac{\sqrt{ \ \ }}{2} \ \)として,
\( \ \sin \ \)なら\( \ \sqrt{ \ \ } \ \)の中身が\( \ 1,2,3 \ \)と\( \ 1 \ \)ずつ増える,
\( \ \cos \ \)なら\( \ \sqrt{ \ \ } \ \)の中身が\( \ 3,2,1 \ \)と\( \ 1 \ \)ずつ減ると覚えましょう。
特別角(\( \ 30^\circ \ \),\( \ 45^\circ \ \),\( \ 60^\circ \ \),)の三角比(\( \ \sin \ \),\( \ \cos \ \))
結局のところ,これら\( \ 3 \ \)つの数値しか登場しないので,覚えておきましょう。
\[
\begin{eqnarray}
\displaystyle \frac{1}{2} ,\displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{\sqrt{3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
これらの数値は,斜辺\( \ 1 \ \)の直角三角形の底辺や高さとなります。


