Contents
弧度法とは
ここまで角度は，\( \ 30^\circ，45^\circ，90^\circ \ \)と書いてきました。これは，円の一周を\( \ 360^\circ \ \)とする方法で，度数法（どすうほう）と呼ばれます。
ここでは，角度を表すもう一つの方法である，弧度法（こどほう）を解説します。
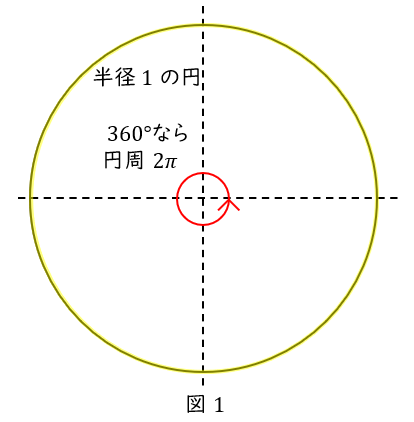
一周を\( \ 2\pi \ \)とする方法です。\( \ 2\pi \ \)とは何かというと，半径\( \ 1 \ \)の円の円周です。
つまり円周の長さ（\( \ 2\pi \ \)）で，角度（\( \ 360^\circ \ \)）を表してしまうのです。
\[
\begin{eqnarray}
360^\circ = 2\pi \\[ 5pt ]
\end{eqnarray}
\]
扇形の曲線部分のことを「弧（こ）」といいますから，弧で角度を表すということで，弧度法です。
長さで角度を表すなんて不思議に思うかもしれません。
似たような例で，家から駅までの距離のことを，徒歩\( \ 5 \ \)分と言いますね。
これは時間で距離を表しています。
同じ理屈で，半径\( \ 1 \ \)の円にできる扇形をイメージして，弧の長さで，角度を表すというわけです。
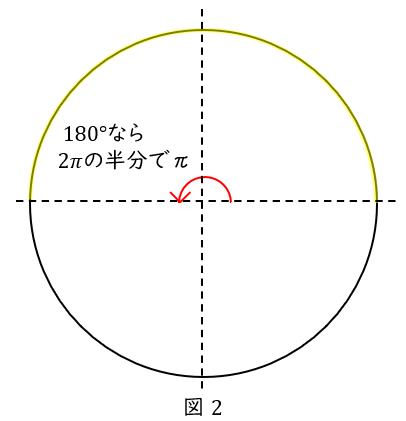
\( \ 180^\circ \ \)を弧度法で表すと？
一周の\( \ 360^\circ \ \)が\( \ 2\pi \ \)なので，その半分の\( \ 180^\circ \ \)なら\( \ \pi \ \)です。
計算式にするとこちらです。
\[
\begin{eqnarray}
\displaystyle \frac{180}{360} \times 2\pi = \displaystyle \frac{1}{2} \times 2\pi = \pi \\[ 5pt ]
\end{eqnarray}
\]
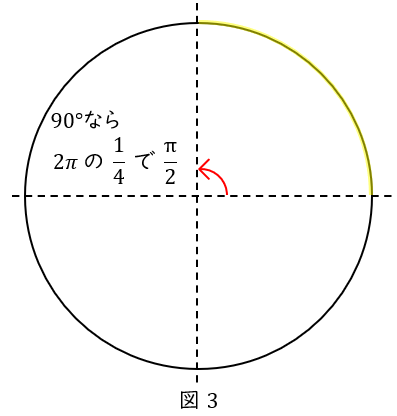
\( \ 90^\circ \ \)を弧度法で表すと？
一周の\( \ 360^\circ \ \)が\( \ 2\pi \ \)なので，その\( \ \displaystyle \frac{1}{4} \ \)の\( \ 90^\circ \ \)なら\( \ \displaystyle \frac{\pi}{2} \ \)です。
計算式にするとこちらです。
\[
\begin{eqnarray}
\displaystyle \frac{90}{360} \times 2\pi = \displaystyle \frac{1}{4} \times 2\pi = \displaystyle \frac{\pi}{2} \\[ 5pt ]
\end{eqnarray}
\]
練習問題で，他の角度についても計算しましょう。
練習問題
表の空欄を埋めましょう。
| 度数法 | \( \ 0^\circ \ \) | \( \ 30^\circ \ \) | \( \ 45^\circ \ \) | \( \ 60^\circ \ \) | \( \ 90^\circ \ \) | \( \ 180^\circ \ \) | \( \ 270^\circ \ \) | \( \ 360^\circ \ \) |
|---|---|---|---|---|---|---|---|---|
| 弧度法 | \( \ \displaystyle \frac{\pi}{2} \ \) | \( \ \pi \ \) | \( \ 2\pi \ \) |
| 度数法 | \( \ 0^\circ \ \) | \( \ 30^\circ \ \) | \( \ 45^\circ \ \) | \( \ 60^\circ \ \) | \( \ 90^\circ \ \) | \( \ 180^\circ \ \) | \( \ 270^\circ \ \) | \( \ 360^\circ \ \) |
|---|---|---|---|---|---|---|---|---|
| 弧度法 | \( \ 0 \ \) | \( \ \displaystyle \frac{\pi}{6} \ \) | \( \ \displaystyle \frac{\pi}{4} \ \) | \( \ \displaystyle \frac{\pi}{3} \ \) | \( \ \displaystyle \frac{\pi}{2} \ \) | \( \ \pi \ \) | \( \ \displaystyle \frac{3}{2} \pi \ \) | \( \ 2\pi \ \) |
ぐるっと一周の\( \ 360^\circ \ \)が\( \ 2\pi \ \)なので，度数法の角度を\( \ x^\circ \ \)として，このように計算します。
\[
\begin{eqnarray}
\displaystyle \frac{x}{360} \times 2\pi = \displaystyle \frac{x \pi}{180} \\[ 5pt ]
\end{eqnarray}
\]
弧度法の出し方
\( \ 90^\circ \ \)までは，
角度\( \ \times \ \)分母の数値\( \ = 180 \ \)
という関係を利用して求めるとよいでしょう。
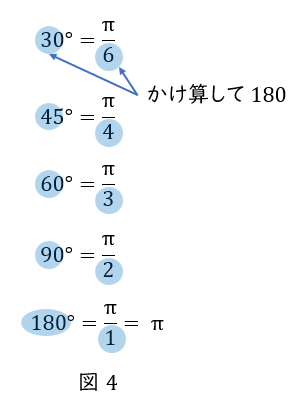
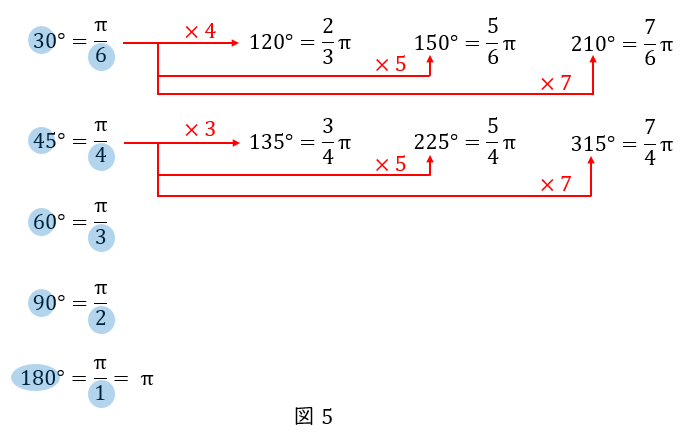
その他の角度の場合は，\( \ 90^\circ \ \)までの角度の何倍かで考えてみましょう。
