Contents
単位円とは
【三角比⑤】の弧度法で,半径\( \ 1 \ \)の円を描きました。
この円を,中心を原点に合わせて,\( \ xy \ \)座標にのせます。
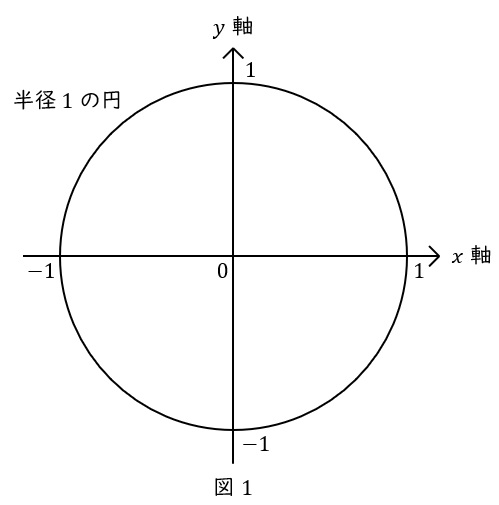
半径が\( \ 1 \ \)ですから,\( \ (x,y)= (1,0),(0,1),(-1,0),(0,-1)\ \)の\( \ 4 \ \)点を通ります。
これを単位円といい,とても大切な考え方となります。
今回は単位円のうち,\( \ x,y \ \)ともに正の値,つまり円の右上の部分の話をします。
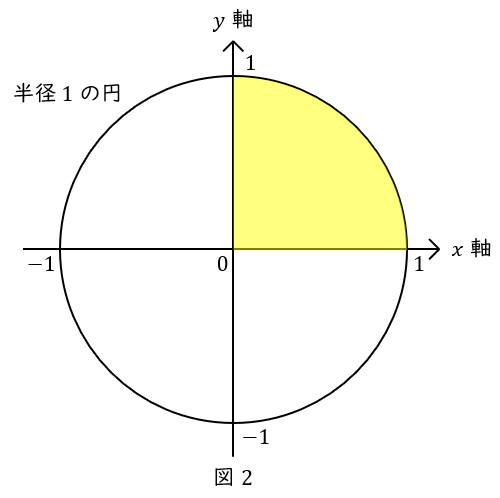
単位円における\( \ \sin \ \)とは
円周上に点をとり(点\( \ \mathrm {P} \ \)とします),原点と結びます。これを斜辺として,\( \ x \ \)軸を底辺として直角三角形を描きます。
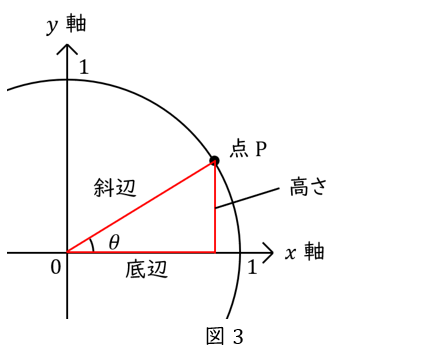
半径\( \ 1 \ \)の円ですから,斜辺は\( \ 1 \ \)です。
\( \ \theta \ \)は\( \ 0 \ \)から\( \ \displaystyle \frac{\pi}{2} \ \)までの様々な値をとります。
\( \ \displaystyle \frac{\pi}{2} \ \)というのは\( \ 90^\circ \ \)のことですね。
ここで,\( \ \sin \ \)とは何だったでしょうか? “斜辺\( \ 1 \ \)の直角三角形の高さ” でしたね。覚え方は「たかさ,さいん」です。
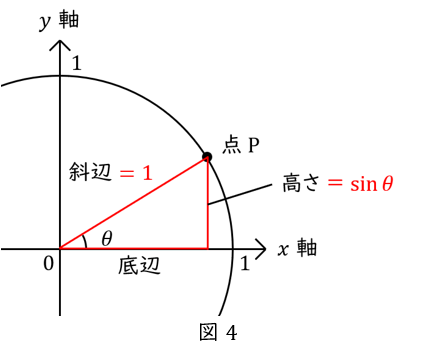
ということは,\( \ x \ \)軸から\( \ \sin \theta \ \)だけ上がったところに点\( \ \mathrm {P} \ \)があるので,点\( \ \mathrm {P} \ \)の\( \ y \ \)座標は\( \ \sin \theta \ \)です。
単位円における\( \ \cos \ \)とは
同じように,\( \ \cos \ \)とは斜辺\( \ 1 \ \)の直角三角形の底辺 です。覚え方は「よこ,こさいん」です。
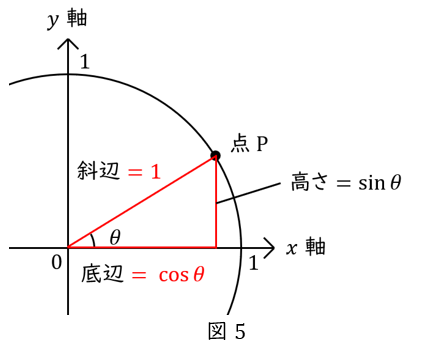
ということは,\( \ y \ \)軸から\( \ \cos \theta \ \)だけ右へ進んだところに点\( \ \mathrm {P} \ \)があるので,点\( \ \mathrm {P} \ \)の\( \ x \ \)座標は\( \ \cos \theta \ \)です。
単位円上の点\( \ \mathrm {P} \ \)の座標は\( \ \sin \ \)と\( \ \cos \ \)で表せる
つまり,円周上の点\( \ \mathrm {P} \ \)の座標は\( \ (\cos \theta,\sin \theta ) \ \)となります。
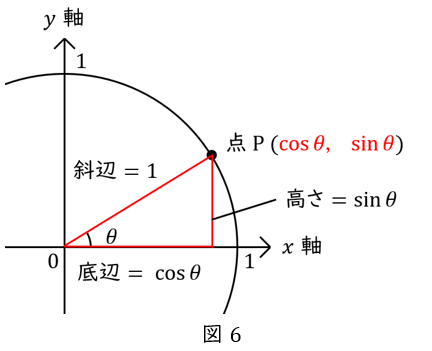
ここで,三角形を消しましょう。
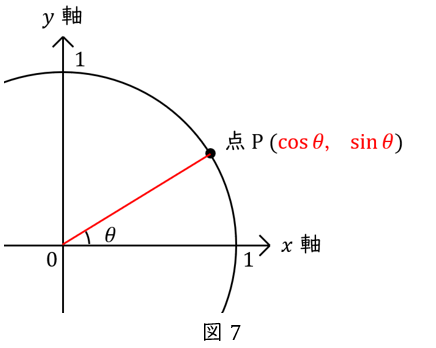
半径\( \ 1 \ \)の円周上にある点を点\( \ \mathrm {P} \ \)として,原点と点\( \ \mathrm {P} \ \)を結ぶ線をひきます。
この線と\( \ x \ \)軸が作る角度を\( \ \theta \ \)とします。
このとき,点\( \ \mathrm {P} \ \)の座標は\( \ (\cos \theta,\sin \theta ) \ \)です。
練習問題で慣れていきましょう。
練習問題
単位円において\( \ \theta \ \)が次の角度のとき,円周上の点\( \ \mathrm {P} \ \)の座標を求め,表の空欄を埋めましょう。
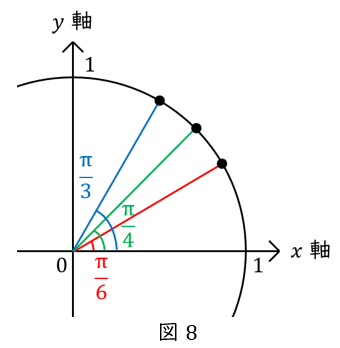
| \( \ \theta \ \) | \( \ \displaystyle \frac{\pi}{6} \ \) | \( \ \displaystyle \frac{\pi}{4} \ \) | \( \ \displaystyle \frac{\pi}{3} \ \) |
|---|---|---|---|
| \( \ (x,y) \ \) |
【三角比⑤】の練習問題と同様に,特別角の三角形を描いて答えを求める方法が一般的です。
しかし,それは既に解説しておりますので,別の考え方を紹介します。
特別角の直角三角形で覚えるべき数値,
\[
\begin{eqnarray}
\displaystyle \frac{1}{2} ,\displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{\sqrt{3}}{2} \\[ 5pt ]
\end{eqnarray}
\]
を利用します。
点\( \ \mathrm {P} \ \)の座標は\( \ (\cos \theta,\sin \theta ) \ \)です。
\( \ x \ \)座標,つまり\( \ \cos \theta \ \)から考えてみましょう。
\( \ \theta \ \)が\( \ 0 \ \)のとき,\( \ x \ \)座標は\( \ 1 \ \),
\( \ \theta \ \)が\( \ \displaystyle \frac{\pi}{2} \ \)のとき,\( \ x \ \)座標は\( \ 0 \ \)です。
つまり\( \ \theta \ \)が\( \ 0 \ \)から\( \ \displaystyle \frac{\pi}{2} \ \)になるにつれて,\( \ x \ \)座標は\( \ 1 \ \)から\( \ 0 \ \)に減少します。
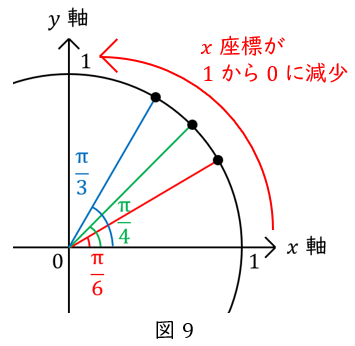
【三角比④】より,特別角の直角三角形で覚えるべき数値は,\( \ \displaystyle \frac{1}{2} ,\displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{\sqrt{3}}{2} \ \)でした。
これを大きい順に並べると,\( \ \displaystyle \frac{\sqrt{3}}{2} ,\displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{1}{2} \ \)ですから,表の\( \ x \ \)座標はこうなります。
| \( \ \theta \ \) | \( \ \displaystyle \frac{\pi}{6} \ \) | \( \ \displaystyle \frac{\pi}{4} \ \) | \( \ \displaystyle \frac{\pi}{3} \ \) |
|---|---|---|---|
| \( \ (x,y) \ \) | \( \ ( \displaystyle \frac{\sqrt{3}}{2} ,y) \ \) | \( \ ( \displaystyle \frac{\sqrt{2}}{2} ,y) \ \) | \( \ ( \displaystyle \frac{1}{2} ,y) \ \) |
続いて\( \ y \ \)座標,つまり\( \ \sin \theta \ \)を考えます。
\( \ \theta \ \)が\( \ 0 \ \)のとき,\( \ y \ \)座標は\( \ 0 \ \),
\( \ \theta \ \)が\( \ \displaystyle \frac{\pi}{2} \ \)のとき,\( \ y \ \)座標は\( \ 1 \ \)です。
つまり\( \ \theta \ \)が\( \ 0 \ \)から\( \ \displaystyle \frac{\pi}{2} \ \)になるにつれて,\( \ y \ \)座標は\( \ 0 \ \)から\( \ 1 \ \)に増加します。
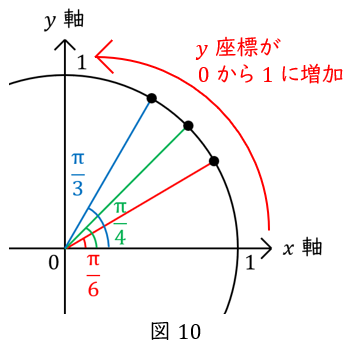
【三角比④】より,特別角の直角三角形で覚えるべき数値は,\( \ \displaystyle \frac{1}{2} ,\displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{\sqrt{3}}{2} \ \)でした。
これを小さい順に並べると,\( \ \displaystyle \frac{1}{2} ,\displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{\sqrt{3}}{2} \ \)ですから,表の\( \ y \ \)座標を埋めて,答えはこちらです。
| \( \ \theta \ \) | \( \ \displaystyle \frac{\pi}{6} \ \) | \( \ \displaystyle \frac{\pi}{4} \ \) | \( \ \displaystyle \frac{\pi}{3} \ \) |
|---|---|---|---|
| \( \ (x,y) \ \) | \( \ ( \displaystyle \frac{\sqrt{3}}{2} ,\displaystyle \frac{1}{2}) \ \) | \( \ ( \displaystyle \frac{\sqrt{2}}{2} ,\displaystyle \frac{\sqrt{2}}{2}) \ \) | \( \ ( \displaystyle \frac{1}{2} ,\displaystyle \frac{\sqrt{3}}{2} ) \ \) |



