《機械》〈パワーエレクトロニクス〉[R04:問5]PWM制御三相インバータとその応用に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，$ \ \mathrm {PWM} \ $制御三相電圧形インバータとその応用に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

三角波比較正弦波$ \ \mathrm {PWM} \ $制御を用いた三相電圧形インバータは，インバータが出力する交流電圧の$ \ \fbox {　（１）　} \ $より直流電圧を十分に高くすることにより，交流電流を制御することができる。したがって，この$ \ \mathrm {PWM} \ $制御三相電圧形インバータ(以降，変換器と呼ぶ)は$ \ \fbox {　（２）　} \ $に電力を制御できるので，種々の分野で使われている。

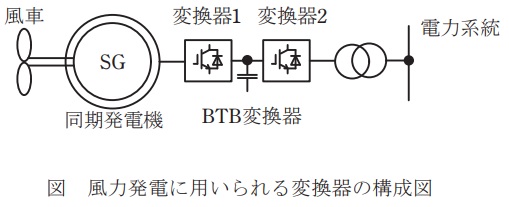
図は風力発電に用いられる変換器の構成図であり，風車のロータに直結した同期発電機$ \ \mathrm {SG} \ $に，変換器$ \ 1 \ $と変換器$ \ 2 \ $からなる$ \ \mathrm {BTB} \ $変換器を接続した構成である。変換器$ \ 1 \ $が$ \ \fbox {　（３）　} \ $周波数の交流電力を直流に変換し，変換器$ \ 2 \ $が直流電力を電力系統周波数の交流に変換する。風車入力エネルギーは羽根の面積を一定とすれば風速の $ \ \fbox {　（４）　} \ $に比例することが知られていて，風速に対して発電できる最大電力とそのときの発電機の回転速度が求まる。したがって，変換器$ \ 1 \ $は$ \ \fbox {　（５）　} \ $を行うことが一般的である。また，変換器$ \ 2 \ $は$ \ \fbox {　（６）　} \ $を検出し，これが一定となるように有効電力を操作する。さらに，変換器$ \ 2 \ $は，電力系統の交流電圧位相に対して，$ \ \fbox {　（７）　} \ $成分の交流電流を流すことにより，上記の有効電力ばかりでなく電力系統の無効電力も制御することができるので，系統電圧の安定化に寄与できるという特徴がある。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　発電機電圧制御　　　　　&（ロ）&　交流から直流へ一方向 \\[ 5pt ] &（ハ）&　直流電流値　　　　　&（ニ）&　発電電力制御 \\[ 5pt ] &（ホ）&　直流から交流へ一方向　　　　　&（ヘ）&　直流電圧値 \\[ 5pt ] &（ト）&　相電圧波高値　　　　　&（チ）&　回転数によらず一定の \\[ 5pt ] &（リ）&　\frac {1}{2} \ 乗　　　　　&（ヌ）&　線間電圧波高値 \\[ 5pt ] &（ル）&　回転数により変動する　　　　　　　　　&（ヲ）&　3 \ 乗 \\[ 5pt ] &（ワ）&　線間電圧実効値　　　　　&（カ）&　直流と交流の間で双方向 \\[ 5pt ] &（ヨ）&　同相の　　　　　&（タ）&　\pi \ 位相のずれた \\[ 5pt ] &（レ）&　±\frac {\pi }{2} \ 位相のずれた　　　　　&（ソ）&　2 \ 乗 \\[ 5pt ] &（ツ）&　定格回転数に相当する　　　　　&& \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {PWM} \ $制御三相電圧形インバータの特徴と風力発電への応用に関する問題です。
三相インバータの動作メカニズムは必須知識と言って良いと思いますが，この問題は風力発電の知識も必要なところが$ \ 1 \ $種の問題という印象です。

1.三相インバータの回路構成と出力波形
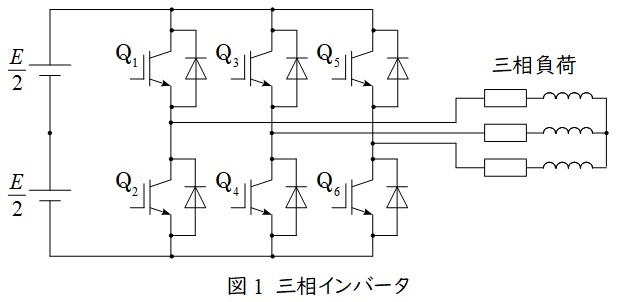
図1に三相インバータ($ \ 2 \ $レベル)の回路構成を示します。
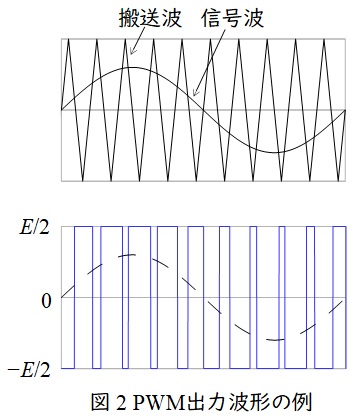
$ \ \mathrm {PWM} \ $制御では図1において，対になっているスイッチ$ \ \mathrm {Q_{1}} \ $と$ \ \mathrm {Q_{2}} \ $，$ \ \mathrm {Q_{3}} \ $と$ \ \mathrm {Q_{4}} \ $，$ \ \mathrm {Q_{5}} \ $と$ \ \mathrm {Q_{6}} \ $を図2のように搬送波（三角波）と信号波を大小比較することでオンオフ切換を行い交流出力を得ます。
図2の例においては信号波＞搬送波のとき$ \ \mathrm {Q_{1}} \ $をオン，$ \ \mathrm {Q_{2}} \ $をオフし，搬送波＞信号波のとき$ \ \mathrm {Q_{1}} \ $をオフ，$ \ \mathrm {Q_{2}} \ $をオンしてパルス幅により出力電圧を調整しています。
そして，信号波を$ \ \displaystyle \frac {2}{3}\pi \ $ずつずらして$ \ \mathrm {Q_{3}} \ $と$ \ \mathrm {Q_{4}} \ $，そして$ \ \mathrm {Q_{5}} \ $と$ \ \mathrm {Q_{6}} \ $をオンオフ制御することで出力に三相交流を得ることができます。

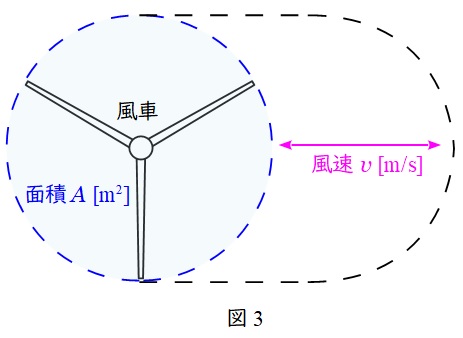
2.風力発電所の出力
図3に示すように，風車の受風面積を$ \ A \ \mathrm {[m^{2}]} \ $，風速を$ \ v \ \mathrm {[m／s]} \ $とすると，単位時間当たりに通過する風の体積$ \ V \ \mathrm {[m^{3}／s]} \ $は，
\[
\begin{eqnarray}
V &=&Av \ \mathrm {[m^{3}／s]} \\[ 5pt ] \end{eqnarray}
\] となります。したがって，単位時間当たりに通過する風の質量$ \ m \ \mathrm {[kg／s]} \ $は，空気の密度を$ \ \rho \ \mathrm {[kg／m^{3}]} \ $とすると，
\[
\begin{eqnarray}
m &=&\rho V \\[ 5pt ] &=&\rho Av \ \mathrm {[kg／s]} \\[ 5pt ] \end{eqnarray}
\] となります。物体の運動エネルギーは$ \ \displaystyle E=\frac {1}{2}mv^{2} \ $であるので，単位時間当たりの風のエネルギー（≒出力）$ \ P \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P &=&\frac {1}{2}mv^{2} \\[ 5pt ] &=&\frac {1}{2}\rho Av^{3} \ \mathrm {[W]}\\[ 5pt ] \end{eqnarray}
\] と求められます。

【解答】

(1)解答：ヌ
題意より解答候補は，（ト）相電圧波高値，（ヌ）線間電圧波高値，（ワ）線間電圧実効値，になると思います。
ワンポイント解説「1.三相インバータの回路構成と出力波形」図2の通り，$ \ \mathrm {PWM} \ $制御においては相電圧波高値が$ \ \displaystyle \frac {E}{2} \ $となり，線間電圧波高値が$ \ \displaystyle \frac {E}{2}-\left( -\frac {E}{2}\right) =E \ $なので直流電圧波高値は，インバータが出力する交流電圧の線間電圧の波高値より高くすることにより，交流電流を制御することができます。

(2)解答：カ
題意より解答候補は，（ロ）交流から直流へ一方向，（ホ）直流から交流へ一方向，（カ）直流と交流の間で双方向，になると思います。
ワンポイント解説「1.三相インバータの回路構成と出力波形」図1に示す通り，三相電圧形インバータは６つのスイッチ素子を使用しており，直流から交流にすることに加えて，逆方向に使用すればブリッジ整流回路として交流を直流にすることも可能となります。したがって，直流と交流の間で双方向に電力を制御できることになります。

(3)解答：ル
題意より解答候補は，（チ）回転数によらず一定の，（ル）回転数により変動する，（ツ）定格回転数に相当する，になると思います。
風車は風速が日々刻々と変化することから，変換器に入力される電力は回転数により変動する交流電力となります。

(4)解答：ヲ
題意より解答候補は，（リ）$ \ \displaystyle \frac {1}{2} \ $乗，（ヲ）$ \ 3 \ $乗，（ソ）$ \ 2 \ $乗，になると思います。
ワンポイント解説「2.風力発電所の出力」の通り，風車入力エネルギーは羽根の面積を一定とすれば風速の$ \ 3 \ $乗に比例します。

(5)解答：ニ
題意より解答候補は，（イ）発電機電圧制御，（ニ）発電電力制御，になると思います。
風力発電は風速の$ \ 3 \ $乗と変動が非常に大きいため，変換器$ \ 1 \ $においては発電電力制御を行うことが一般的となります。

(6)解答：ヘ
題意より解答候補は，（ハ）直流電流値，（ヘ）直流電圧値，になると思います。
変換機$ \ 2 \ $はインバータであり，安定した制御を行うため直流電圧値が一定となるように制御を行うことになります。

(7)解答：レ
題意より解答候補は，（ヨ）同相の，（タ）$ \ \pi \ $位相のずれた，（レ）$ \ \displaystyle ±\frac {\pi }{2} \ $位相のずれた，になると思います。
無効電力は電圧と電流の位相差が$ \ \displaystyle \frac {\pi }{2} \ $の電力なので，電力系統の交流電圧位相に対して，$ \ \displaystyle ±\frac {\pi }{2} \ $位相のずれた成分の交流電流を流すことにより無効電力を制御することが可能となります。