《機械》〈電熱〉[H21:問4]各種電気加熱の原理や特徴に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電気加熱に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句を解答群の中から選び，その記号をマークシートに記入しなさい。

熱の伝達には伝導，対流，放射があり，放射による熱エネルギーを利用した加熱方式に遠赤外加熱がある。ある物質は自身の温度が高い場合，そのもっているエネルギーは電磁波の形で放射される。あらゆる波長の電磁波を吸収し，また，放射する仮想物体（黒体）の放射エネルギーの強さを表す放射発散度を，温度と波長の関係として表したのが$ \ \fbox {　（１）　} \ $の法則である。通常，遠赤外加熱の熱源として使用される物質は，摂氏数百度の温度で，被加熱物のもつ幾つかの大きな熱振動の領域である$ \ \fbox {　（２）　} \ $の波長の遠赤外放射を発生する。

被加熱物が誘電体の場合，電磁波による分極作用を利用したマイクロ波加熱及び誘電加熱がある。特に周波数の高いマイクロ波加熱では，電磁波の浸透深さで加熱範囲が制限され，その浸透深さは波長に比例し，比誘電率の平方根と$ \ \fbox {　（３）　} \ $との積に反比例する。また，純水の場合には，誘電加熱の領域である数十$ \ \mathrm {MHz} \ $以下では誘電損による加熱は極めて効率が低いが，塩分などのイオン源を含むと$ \ \fbox {　（４）　} \ $が増加し有効に加熱される。

周囲の空気，水等の熱エネルギーを利用し，入力した電力エネルギー以上の熱エネルギーを得る加熱方式として，ヒートポンプ方式がある。この方式は，物理的に二つの$ \ \fbox {　（５）　} \ $と二つの可逆断熱変化とからなる逆カルノーサイクルの原理を用いたものである。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　熱伝導率　　　　　&（ロ）&　マクスウェル　　　　　&（ハ）&　可逆等湿変化 \\[ 5pt ] &（ニ）&　数 \ \mathrm {\mu m} \ ～ \ 数十 \ \mathrm {\mu m}　　　　　&（ホ）&　可逆等積変化　　　　　&（ヘ）&　導電率 \\[ 5pt ] &（ト）&　ウィーデマン・フランツ　　　　　　　　&（チ）&　誘電正接　　　　　&（リ）&　誘電体損失係数 \\[ 5pt ] &（ヌ）&　数 \ \mathrm {mm} \ ～ \ 数十 \ \mathrm {mm}　　　　　&（ル）&　透磁率　　　　　&（ヲ）&　可逆等温変化 \\[ 5pt ] &（ワ）&　誘電損角　　　　　&（カ）&　数 \ \mathrm {nm} \ ～ \ 数十 \ \mathrm {nm}　　　　　&（ヨ）&　プランク \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

各種電気加熱の原理や特徴に関する問題です。
非常に範囲が広い内容が出題されていますので，完答することは難しいかもしれません。
本問の場合は完答狙いではなく，３つ以上の空欄が埋められれば良いと考えると良いかと思います。

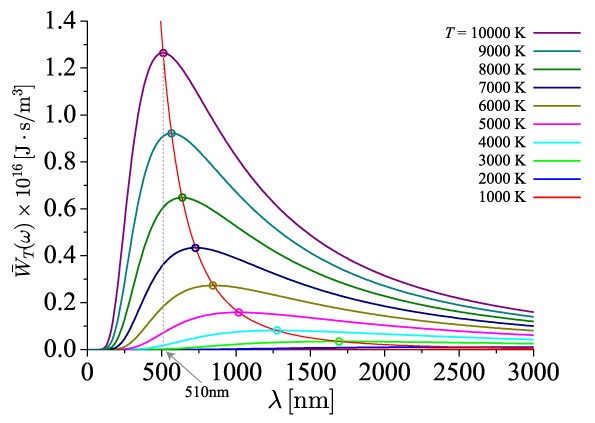
1.プランクの法則
黒体から放射されるエネルギーは黒体の温度によってその大きさが変わり，その波長特性はプランクの法則に従い下図のようになります。
このとき物体表面から放射される放射パワーがピークとなる波長$ \ \lambda _{\mathrm {m}} \ \mathrm {[\mu m]} \ $は温度$ \ T \ \mathrm {[K]} \ $に反比例し，
\[
\begin{eqnarray}
\lambda _{\mathrm {m}} &≒& \frac {2898}{T} \\[ 5pt ] \end{eqnarray}
\] となる関係があり，これをウィーンの変位則といいます。

出典：natural science ホームページ
https://www.natural-science.or.jp/article/20111230191657.php

2.赤外加熱
可視光との境界である波長$ \ 0.78 \ \mathrm {\mu m} \ $以上の赤外線による熱放射を利用して，加熱物を加熱する方法です。物質表面から放射される全放射パワーが絶対温度で表した表面温度の$ \ 4 \ $乗に比例するというステファン・ボルツマンの法則に従って加熱されます。
塗装や印刷の乾燥のほか，食品，電子部品，半導体，プラスチックなどの製造工程においても用いられています。

3.ステファン・ボルツマンの法則
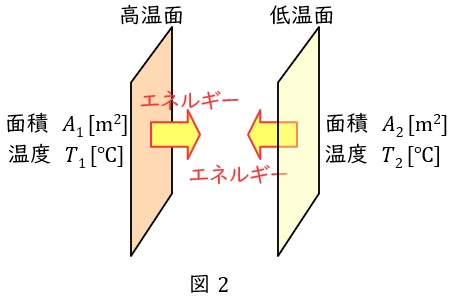
図2のように，面積$ \ A_{1} \ \mathrm {[m^{2}]} \ $，温度$ \ T_{1} \ \mathrm {[K]} \ $の高温面と，面積$ \ A_{2} \ \mathrm {[m^{2}]} \ $，温度$ \ T_{2} \ \mathrm {[K]} \ $の低温面があるとき，$ \ 1 \ $秒当たりに高温面から低温面に伝わるエネルギー$ \ \mathit {\Phi } \ \mathrm {[W]} \ $は，$ \ \varepsilon \ $を放射率，$ \ \sigma \ \mathrm {[W / \left( m^{2}\cdot K^{4}\right) ]} \ $をステファン・ボルツマン定数，$ \ F_{12} \ $を形態係数とすると，
\[
\begin{eqnarray}
\mathit {\Phi } &=& \varepsilon \sigma A_{1}F_{12}\left( T_{1}^{4}-T_{2}^{4}\right) \\[ 5pt ] \end{eqnarray}
\] で求められるという法則です。

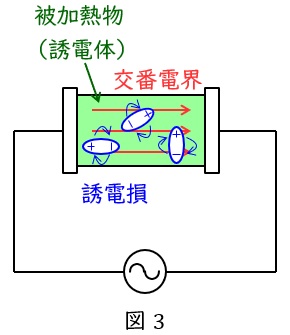
4.誘電加熱
交番電界中に誘電体を置くことによって，誘電体に誘電損が生じ発熱します。電子レンジ（マイクロ波加熱）はこの原理を利用した電化製品の一つです。
図3に示すように，交番電界により被加熱物自体が発熱するため，予熱等も不要で被加熱物内部まで短時間で加熱することができます。また，電磁波の出力により温度調整も容易に行うことができます。
マイクロ波加熱では，電磁波の浸透深さを示す値として密度が半減する電力半減深度$ \ D \ \mathrm {[m]} \ $というものがあり，周波数$ \ f \ \mathrm {[Hz]} \ $，比誘電率$ \ \varepsilon _{\mathrm {r}} \ $，誘電正接$ \ \tan \delta \ $とすると，
\[
\begin{eqnarray}
D &≒& \frac {3.32\times 10^{7}}{f\sqrt {\varepsilon _{\mathrm {r}}}\tan \delta } \\[ 5pt ] \end{eqnarray}
\] で求められます。

5.ヒートポンプの構成機器
ヒートポンプのフローを図4に示します。冷房時が青線，暖房時は赤線の流れとなります。冷房時を例に示します。
　蒸発器：膨張弁からの低温低圧の液を蒸発させ気化させます。
　四方弁：暖房冷房時に圧縮機に流れる媒体の向きを同じにするために向きを変えるものです。
　圧縮機：蒸発器から出た低圧の蒸気を高圧蒸気にします。
　凝縮器：圧縮機で高温高圧となった蒸気を凝縮し，液化させます。
　膨張弁：凝縮器から出た液を膨張し，低温低圧の液にします。

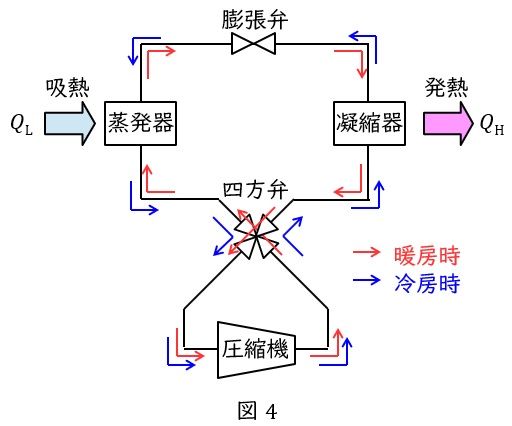
　※図4において，暖房時には熱交換器である蒸発器と凝縮器の役割が逆となります。

【解答】

(1)解答：ヨ
題意より解答候補は，（ロ）マクスウェル，（ト）ウィーデマン・フランツ，（ヨ）プランク，になると思います。
ワンポイント解説「1.プランクの法則」の通り，放射する仮想物体（黒体）の放射エネルギーの強さを表す放射発散度を，温度と波長の関係として表したのはプランクの法則となります。マクスウェルの法則は電磁気の性質を４つの式にまとめたもの，ウィーデマン・フランツは金属の熱伝導率と電気伝導率の比と温度の関係を示したもの，となります。

(2)解答：ニ
題意より解答候補は，（ニ）数$ \ \mathrm {\mu m} \ $～数十$ \ \mathrm {\mu m} \ $，（ヌ）数$ \ \mathrm {mm} \ $～数十$ \ \mathrm {mm} \ $，（カ）数$ \ \mathrm {nm} \ $～数十$ \ \mathrm {nm} \ $，になると思います。
ワンポイント解説「2.赤外加熱」の通り，遠赤外線加熱の熱源として使用される物質は数$ \ \mathrm {\mu m} \ $～数十$ \ \mathrm {\mu m} \ $の波長の遠赤外放射を発生します。

(3)解答：チ
題意より解答候補は，（イ）熱伝導率，（ヘ）導電率，（チ）誘電正接，（リ）誘電体損失係数，（ル）透磁率，（ワ）誘電損角，になると思います。
ワンポイント解説「4.誘電加熱」の通り，電磁波の浸透深さ$ \ D \ \mathrm {[m]} \ $は，周波数$ \ f \ \mathrm {[Hz]} \ $，比誘電率$ \ \varepsilon _{\mathrm {r}} \ $，誘電正接$ \ \tan \delta \ $とすると，
\[
\begin{eqnarray}
D &≒& \frac {3.32\times 10^{7}}{f\sqrt {\varepsilon _{\mathrm {r}}}\tan \delta } \\[ 5pt ] \end{eqnarray}
\] で求められ，比誘電率の平方根と誘電正接の積に反比例します。

(4)解答：ヘ
題意より解答候補は，（イ）熱伝導率，（ヘ）導電率，（チ）誘電正接，（リ）誘電体損失係数，（ル）透磁率，（ワ）誘電損角，になると思います。
誘電損による加熱は電流値に関係するので，導電率が増加すると有効に加熱されます。

(5)解答：ヲ
題意より解答候補は，（ハ）可逆等湿変化，（ホ）可逆等積変化，（ヲ）可逆等温変化，になると思います。
ワンポイント解説「5.ヒートポンプの構成機器」の通り，圧縮機と膨張弁が熱を加えたり放出したりしない可逆断熱変化，蒸発器と凝縮器が気体液体の状態変化で温度が変化しない可逆等温変化となります。