【問題】
【難易度】★★★★★(難しい)
次の文章は,三相電圧形\( \ \mathrm {PWM} \ \)インバータに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
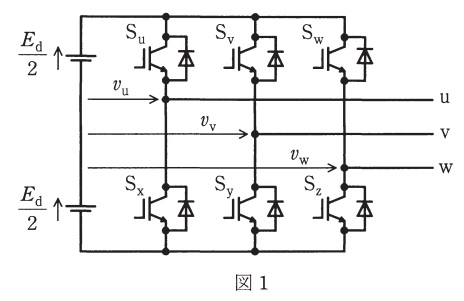
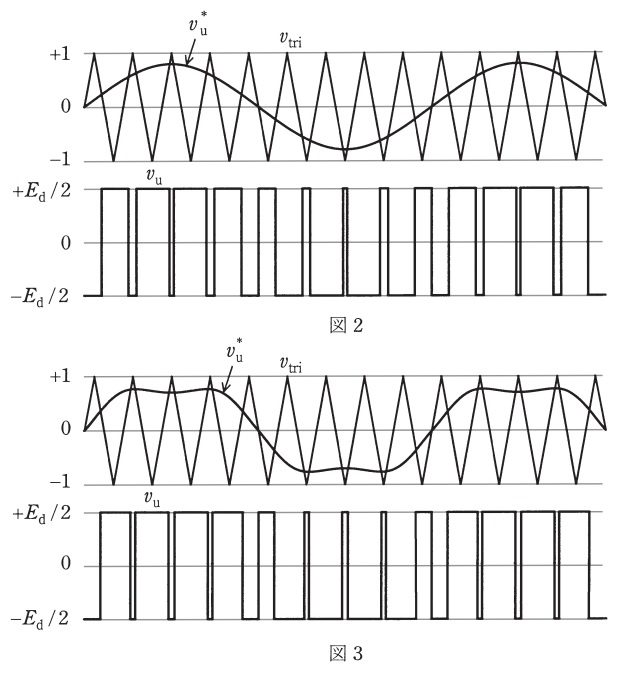
図1の三相電圧形\( \ \mathrm {PWM} \ \)インバータに三角波比較\( \ \mathrm {PWM} \ \)制御を適用した場合の三角波\( \ v_{\mathrm {tri}} \ \)と\( \ \mathrm {u} \ \)相の信号波\( \ v_{\mathrm {u}}^{*} \ \),\( \ \mathrm {u} \ \)相の電圧\( \ v_{\mathrm {u}} \ \)の波形を図2に示す。ここで,\( \ v_{\mathrm {tri}} \ \)の波高値を\( \ \mathrm{1} \ \),直流電圧を\( \ E_{\mathrm {d}} \ \)とする。この制御法では,\( \ v_{\mathrm {tri}} \ \)と\( \ v_{\mathrm {u}}^{*} \ \)とを比較して\( \ \fbox { (1) } \ \)期間に\( \ \mathrm {S}_{\mathrm {u}} \ \)をオンし,それ以外の期間は\( \ \mathrm {S}_{\mathrm {x}} \ \)をオンする。各相の信号波を,基本波角周波数\( \ \omega \ \)の正弦波として次式で与える。
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle v_{\mathrm {u}}^{*}=A\sin \omega t \\[ 5pt ]
\displaystyle v_{\mathrm {v}}^{*}=A\sin \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ]
\displaystyle v_{\mathrm {w}}^{*}=A\sin \left( \omega t+\frac {2}{3}\pi \right)
\end{array}
\right.
\end{eqnarray}
\]
このとき,\( \ 0\lt A ≦ 1 \ \)であれば,\( \ v_{\mathrm {u}} \ \)の\( \ \fbox { (2) } \ \)成分の位相は\( \ v_{\mathrm {u}}^{*} \ \)と同じで,振幅は\( \ A \ \)に比例する。\( \ A=1 \ \)の場合,\( \ v_{\mathrm {u}} \ \)の基本波実効値は\( \ \fbox { (3) } \ \)となる。
ここで,図3のように,\( \ 3 \ \)次高調波成分を重畳した信号波を次式で与える。
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle v_{\mathrm {u}}^{*}=B\sin \omega t+\frac {B}{6}\sin 3\omega t \\[ 5pt ]
\displaystyle v_{\mathrm {v}}^{*}=B\sin \left( \omega t-\frac {2}{3}\pi \right) +\frac {B}{6}\sin 3\omega t \\[ 5pt ]
\displaystyle v_{\mathrm {w}}^{*}=B\sin \left( \omega t+\frac {2}{3}\pi \right) +\frac {B}{6}\sin 3\omega t
\end{array}
\right.
\end{eqnarray}
\]
このとき,\( \ \fbox { (4) } \ \)には\( \ 3 \ \)次高調波成分は現れない。そして,\( \ B \ \)を\( \ \mathrm{1} \ \)よりも大きく,\( \ B=\fbox { (5) } \ \)まで増加しても,\( \ v_{\mathrm {u}} \ \)の基本波実効値は\( \ B \ \)に比例する。
〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {E_{\mathrm {d}}}{\sqrt {3}} &(ロ)& \frac {6}{5} &(ハ)& \frac {v_{\mathrm {u}}+v_{\mathrm {v}}+v_{\mathrm {w}}}{3} \\[ 5pt ]
&(ニ)& \frac {4}{\pi } &(ホ)& \frac {2}{\sqrt {3}} &(ヘ)& 三角波周波数 \\[ 5pt ]
&(ト)& \frac {E_{\mathrm {d}}}{2\sqrt {2}} &(チ)& \frac {E_{\mathrm {d}}}{2} &(リ)& v_{\mathrm {tri}}が大きい \\[ 5pt ]
&(ヌ)& v_{\mathrm {u}} &(ル)& 側帯波周波数 &(ヲ)& v_{\mathrm {u}}-v_{\mathrm {v}} \\[ 5pt ]
&(ワ)& v_{\mathrm {u}}^{*}が大きい &(カ)& 信号波周波数 &(ヨ)& v_{\mathrm {u}}^{*}とv_{\mathrm {tri}}が等しい
\end{eqnarray}
\]
【ワンポイント解説】
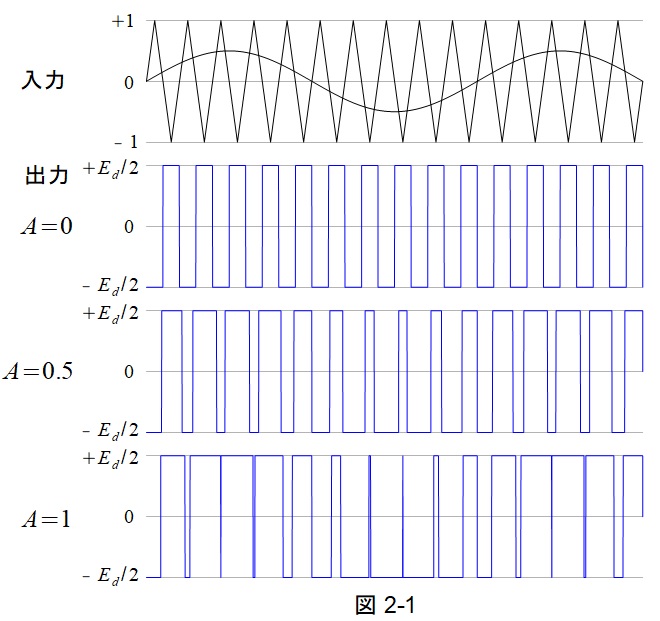
パワーエレクトロニクスの問題は,どのような出力になるかイメージできるかどうかが重要です。参考として図2-1に\( \ A \ \)の値が変化した時の出力波形の波形を示します。
【解答】
(1)解答:ワ
図1において,\( \ v_{\mathrm {u}} \ \)の電位は\( \ \mathrm {S}_{\mathrm {u}} \ \)が\( \ \mathrm {ON} \ \)の時\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \),\( \ \mathrm {S}_{\mathrm {x}} \ \)が\( \ \mathrm {ON} \ \)の時\( \ \displaystyle -\frac {E_{\mathrm {d}}}{2} \ \)となる。
図2で出力が\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)となるのは,\( \ v_{\mathrm {u}}^{*} \gt v_{\mathrm {tri}} \ \)となる時である。よって,\( \ \mathrm {S}_{\mathrm {u}} \ \)を\( \ \mathrm {ON} \ \)するのは\( \ v_{\mathrm {u}}^{*} \gt v_{\mathrm {tri}} \ \)の期間である。
(2)解答:カ
図2-1に示すように,\( \ \mathrm {PWM} \ \)制御において\( \ 0\lt A ≦ 1 \ \)であれば\( \ v_{\mathrm {u}} \ \)の信号波周波数成分の位相は\( \ v_{\mathrm {u}}^{*} \ \)と同じとなります。
(3)解答:ト
周波数成分の出力は
\[
\begin{eqnarray}
v_{\mathrm {u}} &=& \frac {E_{\mathrm {d}}}{2}v_{\mathrm {u}}^{*} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{2}A\sin \omega t
\end{eqnarray}
\]
となり,実効値は振幅の\( \ \displaystyle \frac {1}{\sqrt {2}} \ \)倍となるので,
\[
\begin{eqnarray}
\frac {E_{\mathrm {d}}A}{2\sqrt {2}}
\end{eqnarray}
\]
となります。よって,\( \ A=1 \ \)の時の実効値は
\[
\begin{eqnarray}
\frac {E_{\mathrm {d}}}{2\sqrt {2}}
\end{eqnarray}
\]
となります。
(4)解答:ヲ
\( \ 3 \ \)次高調波成分を重畳した信号波の出力は,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle v_{\mathrm {u}}=\frac {E_{\mathrm {d}}}{2}B\sin \omega t+\frac {E_{\mathrm {d}}}{2}\frac {B}{6}\sin 3\omega t \\[ 5pt ]
\displaystyle v_{\mathrm {v}}=\frac {E_{\mathrm {d}}}{2}B\sin \left( \omega t-\frac {2}{3}\pi \right) +\frac {E_{\mathrm {d}}}{2}\frac {B}{6}\sin 3\omega t \\[ 5pt ]
\displaystyle v_{\mathrm {w}}=\frac {E_{\mathrm {d}}}{2}B\sin \left( \omega t+\frac {2}{3}\pi \right) +\frac {E_{\mathrm {d}}}{2}\frac {B}{6}\sin 3\omega t
\end{array}
\right.
\end{eqnarray}
\]
となる。これより,\( \ v_{\mathrm {u}}-v_{\mathrm {v}} \ \)は\( \ 3 \ \)次高調波成分が現れないことが分かる。
(5)解答:ホ
\( \ \mathrm {PWM} \ \)の出力波形が\( \ B \ \)に比例するためには信号波\( \ v_{\mathrm {u}}^{*} \ \)の最大値が\( \ 1 \ \)を超えないようにしなければならない。ここで,\( \ v_{\mathrm {u}}^{*} \ \)の最大値を求めるため\( \ v_{\mathrm {u}}^{*} \ \)を微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}v_{\mathrm {u}}^{*}}{\mathrm {d}\omega t}=B\cos \omega t+\frac {B}{2}\cos 3\omega t \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}v_{\mathrm {u}}^{*}}{\mathrm {d}\omega t}=0 \ \)となる\( \ \omega t \ \)を求めると,
\[
\begin{eqnarray}
B\cos \omega t+\frac {B}{2}\cos 3\omega t &=& 0 \\[ 5pt ]
B\cos \omega t+\frac {B}{2}\cos (2\omega t +\omega t) &=& 0 \\[ 5pt ]
B\cos \omega t+\frac {B}{2}(\cos 2\omega t \cos \omega t-\sin 2\omega t \sin \omega t ) &=& 0 \\[ 5pt ]
B\cos \omega t+\frac {B}{2}\left \{(\cos ^{2}\omega t-\sin ^{2}\omega t)\cos \omega t-2\sin \omega t \cos \omega t \sin \omega t \right\} &=& 0 \\[ 5pt ]
B\cos \omega t+\frac {B}{2}(\cos ^{3}\omega t-3\sin ^{2}\omega t\cos \omega t) &=& 0 \\[ 5pt ]
B\cos \omega t+\frac {B}{2}\left \{\cos ^{3}\omega t-3(1-\cos ^{2}\omega t) \cos \omega t\right\} &=& 0 \\[ 5pt ]
B\cos \omega t+\frac {B}{2}(4\cos ^{3}\omega t-3 \cos \omega t) &=& 0 \\[ 5pt ]
2B\cos ^{3}\omega t-\frac {B}{2} \cos \omega t &=& 0 \\[ 5pt ]
\cos \omega t (2B\cos \omega t+1)(2B\cos \omega t+1) &=& 0 \\[ 5pt ]
\cos \omega t &=& 0,\pm \frac {1}{2} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \displaystyle 0 ≦ \omega t ≦ \frac {1}{2} \ \)においては,
\[
\begin{eqnarray}
\omega t &=& \frac {\pi }{3},\frac {\pi }{2},\frac {2\pi }{3} \\[ 5pt ]
\end{eqnarray}
\]
となる。図3より,\( \ v_{\mathrm {u}}^{*} \ \)が最大値となるのは\( \ \displaystyle \omega t = \frac {\pi }{3},\frac {2\pi }{3} \ \)の時であるので,\( \ v_{\mathrm {u}}^{*} \ \)の最大値は,
\[
\begin{eqnarray}
v_{\mathrm {u}}^{*} \left( \frac {\pi}{3} \right) &=&B\sin \frac {\pi}{3}+\frac {B}{6}\sin \left( 3\cdot \frac {\pi}{3}\right) \\[ 5pt ]
&=&\frac {\sqrt {3}}{2}B \\[ 5pt ]
\end{eqnarray}
\]
となる。よって\( \ v_{u}^{*} \ \)が\( \ 1 \ \)を超えない\( \ B \ \)の最大値は,
\[
\begin{eqnarray}
B=\frac {2}{\sqrt {3}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん