《機械》〈変圧器〉[R03:問2]変圧器の電源投入時の現象に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，変圧器の電源投入時の現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

無励磁状態の変圧器を電源に接続する場合，電源投入時の電圧位相や鉄心内の残留磁束の状態によっては\( \ \fbox {　 （１） 　} \ \)現象を原因とする大きな電流が過渡的に流入する場合がある。この電流を励磁突入電流という。

変圧器に電源が投入されると，鉄心内の磁束は，投入前における鉄心内の残留磁束を初期値として，印加電圧の\( \ \fbox {　 （２） 　} \ \)値に比例した波形になる。鉄心内の残留磁束が無い状態において，印加電圧\( \ 0 \ \)の瞬間に投入されると，半周期の間に鉄心内磁束は定常状態の磁束最大値の\( \ 2 \ \)倍近くまで増加し，鉄心の飽和磁束密度を超えると過渡的に大きな電流が流入する。また，電源投入時に鉄心内に残留磁束がある状態では，それが印加電圧による磁束の変化方向と\( \ \fbox {　 （３） 　} \ \)方向に重畳する場合には，鉄心内の磁束が定常状態の磁束最大値の\( \ 2 \ \)倍を超え，励磁突入電流の波高値はさらに高くなる。

この励磁突入電流を抑制するため，投入前に残留磁束の消去や，\( \ \fbox {　 （４） 　} \ \)の制御などを行うことがある。

投入後，磁束は徐々に定常状態に戻っていき，それとともに励磁突入電流も減衰して通常の励磁電流に落ち着く。この継続時間は，回路のインダクタンスと抵抗などによって決まり，一般に変圧器容量が大きく\( \ \fbox {　 （５） 　} \ \)。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　磁気誘導　　　　　&（ロ）&　反対　　　　　&（ハ）&　磁歪振動 \\[ 5pt ] &（ニ）&　積分　　　　　&（ホ）&　直角　　　　　&（ヘ）&　なるほど短くなる \\[ 5pt ] &（ト）&　鉄心振動　　　　　&（チ）&　投入位相　　　　　&（リ）&　なるほど長くなる \\[ 5pt ] &（ヌ）&　同一　　　　　&（ル）&　実効　　　　　&（ヲ）&　なっても変わらない \\[ 5pt ] &（ワ）&　電源周波数　　　　　　　&（カ）&　磁気飽和　　　　　　　&（ヨ）&　微分 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

変圧器の励磁突入電流のメカニズムに関する問題です。
このまま二次試験の論説問題として出題されても良いような問題で，電力管理科目の範囲でも出題される可能性がある問題と言えます。

1.励磁突入電流
変圧器を遮断器投入によって電路に接続すると，投入時の電圧の位相によっては定格電流の数倍から十数倍の大きな励磁電流が流れることがあり，これを励磁突入電流といいます。
ファラデーの電磁誘導の法則より，電圧\( \ e \ \mathrm {[V]} \ \)と磁束\( \ \phi \ \mathrm {[Wb]} \ \)には，
\[
\begin{eqnarray}
e&=&-N\frac {\mathrm {d}\phi }{\mathrm {d}t} \\[ 5pt ] N\mathrm {d}\phi &=&-e\mathrm {d}t \\[ 5pt ] N\int \mathrm {d}\phi &=&-\int e\mathrm {d}t \\[ 5pt ] N\phi &=&-\int e\mathrm {d}t \\[ 5pt ] \end{eqnarray}
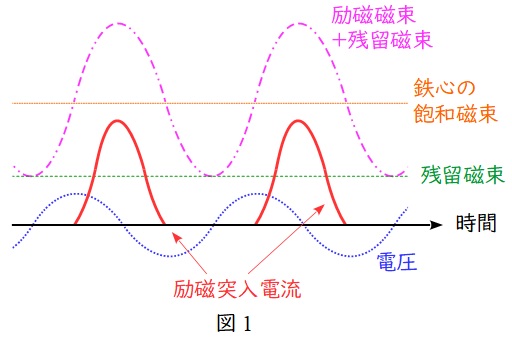
\] という積分の関係があるため，仮に正弦波の電圧が加わっている状態で図1の＋から－に切り替わる\( \ 0 \ \mathrm {[V]} \ \)付近で投入された場合には，最大で\( \ 2 \ \)倍程度の磁束が発生し，残留磁束の影響でさらに磁束が大きくなると鉄心の飽和磁束密度を超えて大きな励磁電流が流れる可能性があります。
したがって，励磁突入電流の対策としては励磁磁束と残留磁束の合計値を小さくすれば良いので，残留磁束の消去や投入位相の制御等が有効となります。

【関連する「電気の神髄」記事】

　　励磁突入電流の理論

【解答】

(1)解答：カ
題意より解答候補は，（イ）磁気誘導，（ハ）磁歪振動，（ト）鉄心振動，（カ）磁気飽和，になると思います。
ワンポイント解説「1.励磁突入電流」の通り，励磁突入電流の原因となるのは磁気飽和現象となります。

(2)解答：ニ
題意より解答候補は，（ニ）積分，（ル）実効，（ヨ）微分，等になると思います。
ワンポイント解説「1.励磁突入電流」の通り，印加電圧による励磁磁束は印加電圧の積分値に比例した値が誘起されます。

(3)解答：ヌ
題意より解答候補は，（ホ）直角，（ロ）反対，（ヌ）同一，になると思います。
ワンポイント解説「1.励磁突入電流」図1の通り，印加電圧による磁束と残留磁束が同一方向に重畳する場合には，励磁突入電流の波高値はさらに高くなります。

(4)解答：チ
題意より解答候補は，（チ）投入位相，（ワ）電源周波数，になると思います。
ワンポイント解説「1.励磁突入電流」の通り，電圧が＋から－に切り替わる\( \ 0 \ \mathrm {[V]} \ \)付近となる位相で投入されると励磁突入電流が大きくなるため，投入位相を制御することが効果的となります。

(5)解答：リ
題意より解答候補は，（ヘ）なるほど短くなる，（リ）なるほど長くなる，（ヲ）なっても変わらない，になると思います。
一般に，\( \ RL \ \)直列回路の時定数は\( \ \displaystyle \tau =\frac {L}{R} \ \)であるため，継続時間は変圧器容量が大きく\( \ L \ \)の比率が高くなるほど長くなる傾向があります。