【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,半導体電力変換装置に用いる変換装置用変圧器に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は数値を解答群の中から選びなさい。
三相ブリッジ接続の他励サイリスタ変換装置に用いる変圧器において,一次巻線(交流巻線)を三相とも短絡し,二次巻線(直流巻線)の任意の\( \ 2 \ \)端子間に定格周波数の正弦波電流を通電したときの電圧及び電流から算出される全リアクタンスは,\( \ \fbox { (1) } \ \)である。この値が十分に小さく,かつ,変換装置の直流電流のリプルが十分に小さいとき,この変圧器を変換装置に用いたときの二次電流(直流側電流)波形は,\( \ 120° \ \)通電の\( \ \fbox { (2) } \ \)状になる。このため,二次電流の実効値は,その基本波の実効値\( \ \displaystyle \frac {\sqrt {6}}{\pi }I_{\mathrm {d}} \ \)(\( \ I_{\mathrm {d}} \ \)は直流電流の値)に対して約\( \ \fbox { (3) } \ \mathrm {[%]} \ \)大きくなる。
\( \ \mathrm {PWM} \ \)制御された三相ブリッジ接続の電圧形自励交直変換装置に用いる変圧器を考える。二次巻線に加わる線間電圧は,変圧器が変換器に直接接続されているとき,変換装置の\( \ \fbox { (4) } \ \)を振幅とした\( \ \mathrm {PWM} \ \)波形となる。
電圧形自励交直変換装置に用いる変圧器は,変換器が発生する電圧で二次巻線が励磁されるので他励用に比べて直流偏磁する可能性が高い。直流偏磁を抑制するための対策の一つの方法は,変圧器に偏磁が生じないように\( \ \fbox { (5) } \ \)を変換器で制御することである。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 転流リアクタンス &(ロ)& 9.6 &(ハ)& 正弦波 \\[ 5pt ]
&(ニ)& 三角波 &(ホ)& 実効リアクタンス &(ヘ)& 1.2 \\[ 5pt ]
&(ト)& 4.7 &(チ)& 二次電圧又は電流 &(リ)& 交流電力 \\[ 5pt ]
&(ヌ)& 直流電圧 &(ル)& 一次電圧又は電流 &(ヲ)& 方形波 \\[ 5pt ]
&(ワ)& 短絡リアクタンス &(カ)& 交流電源電圧のピーク値 &(ヨ)& 直流電圧の \ \frac {1}{2} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
半導体電力変換装置に用いる変換装置用変圧器に関する問題です。
恐らくサイクロコンバータの内容を問いたい問題と思いますが,図が与えられておらず,文章を読み解きながら,三相サイリスタブリッジ整流回路と三相インバータの内容を考えていかなければならないので,かなり厳しい問題であったかなと思います。
1.三相サイリスタブリッジ整流回路の平均出力電圧\( \ E_{\mathrm {d}} \ \)
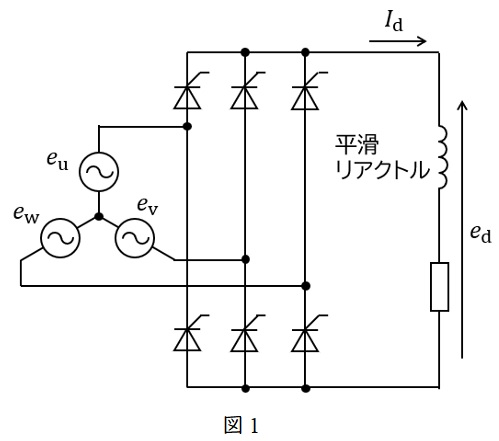
図1のような三相サイリスタブリッジ整流回路について考えます。
ただし,電源の電圧は\( \ e_{\mathrm {u}} \ \)を基準として,
\[
\begin{eqnarray}
e_{\mathrm {u}} &=&\sqrt {2}E \sin \theta \\[ 5pt ]
e_{\mathrm {v}} &=&\sqrt {2}E \sin \left( \theta -\frac {2}{3}\pi \right) \\[ 5pt ]
e_{\mathrm {w}} &=&\sqrt {2}E \sin \left( \theta -\frac {4}{3}\pi \right) \\[ 5pt ]
\end{eqnarray}
\]
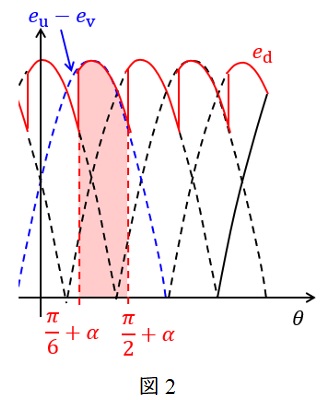
とします。サイリスタの制御角を\( \ \alpha \ \)とすると,出力電圧は図2のようになります。
このとき,出力電圧は周期\( \ \displaystyle \frac {\pi }{3} \ \)で繰り返しているので,その平均出力電圧\( \ E_{\mathrm {d}} \ \)は図2で示した領域の平均値を求めればよいことになります。
図2において,
\[
\begin{eqnarray}
e_{\mathrm {u}} -e_{\mathrm {v}}&=&\sqrt {2}E \sin \theta -\sqrt {2}E \sin \left( \theta -\frac {2}{3}\pi \right) \\[ 5pt ]
&=&\sqrt {2}E\times 2\cos \left( \theta -\frac {\pi }{3}\right)\sin \frac {\pi}{3} \left( ∵和積の公式\right) \\[ 5pt ]
&=&\sqrt {2}E\times 2\cos \left( \theta -\frac {\pi }{3}\right) \cdot \frac {\sqrt {3}}{2} \\[ 5pt ]
&=&\sqrt {6}E\cos \left( \theta -\frac {\pi }{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので平均出力電圧\( \ E_{\mathrm {d}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {1}{\displaystyle \frac {\pi }{3}}\int _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha }\sqrt {6}E\cos \left( \theta -\frac {\pi }{3}\right) \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\int _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha }\cos \left( \theta -\frac {\pi }{3}\right) \mathrm {d}\theta \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\left[ \sin \left( \theta -\frac {\pi }{3}\right) \right] _{\frac {\pi }{6}+\alpha }^{\frac {\pi }{2}+\alpha } \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi }\left\{ \sin \left( \alpha +\frac {\pi }{6}\right) -\sin \left( \alpha -\frac {\pi }{6}\right) \right\} \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi } \cdot 2\cos \alpha \sin \frac {\pi }{6} \left( ∵和積の公式\right) \\[ 5pt ]
&=&\frac {3\sqrt {6}E}{\pi } \cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
となります。(和積の公式はこちら)ここで,電源の線間電圧\( \ V \ \)の大きさは相電圧の\( \ \sqrt {3} \ \)倍の大きさなので,
\[
\begin{eqnarray}
E_{\mathrm {d}}&=&\frac {3\sqrt {2}V}{\pi } \cos \alpha \\[ 5pt ]
&≒&1.35V\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.三相インバータの動作
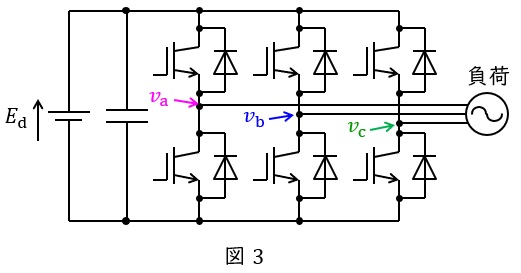
三相インバータは直流から交流を得る回路で,図3のような\( \ 6 \ \)つのスイッチで構成されています。
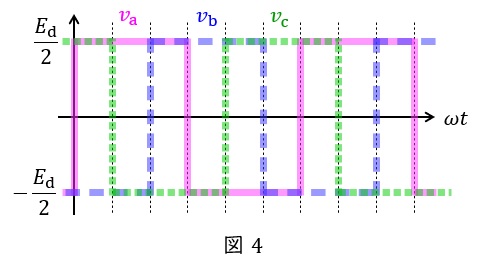
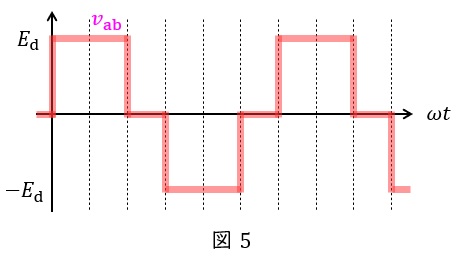
例えば,対応する正負のスイッチを\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずらしてオンオフ制御すると,図4のように\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずれた方形波が得られ,線間電圧を取れば図5のようなより正弦波に近い波形が得られます。
このとき,線間電圧の実効値\( \ V \ \)は,
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }E_{\mathrm {d}}^{2}\mathrm {d}\theta } \\[ 5pt ]
&=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }1\mathrm {d}\theta } \\[ 5pt ]
&=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left[ \theta \right] _{0}^{\frac {2}{3}\pi }} \\[ 5pt ]
&=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left( \frac {2}{3}\pi -0 \right) } \\[ 5pt ]
&=&\sqrt {\frac {2}{3}}E_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:イ
題意より解答候補は,(イ)転流リアクタンス,(ホ)実効リアクタンス,(ワ)短絡リアクタンス,になると思います。
一次巻線(交流巻線)を三相とも短絡し,二次巻線(直流巻線)の任意の\( \ 2 \ \)端子間に定格周波数の正弦波電流を通電したときの電圧及び電流から算出される全リアクタンスは,変圧器二相分のリアクタンスとなり,これは転流の際の転流リアクタンスと同じ大きさとなります。
(2)解答:ヲ
題意より解答候補は,(ハ)正弦波,(ニ)三角波,(ヲ)方形波,になると思います。
転流リアクタンスが十分に小さく,かつ,変換装置の直流電流のリプルが十分に小さいとき,すなわち理想的な状態では二次電流(直流側電流) の\( \ 1 \ \)相分の波形は,\( \ 120° \ \)通電の方形波となります。
(3)解答:ト
題意より解答候補は,(ロ)\( \ 9.6 \ \),(ヘ)\( \ 1.2 \ \),(ト)\( \ 4.7 \ \),になると思います。振幅が\( \ E_{\mathrm {d}} \ \)で\( \ 120° \ \)通電の方形波の実効値\( \ I \ \)は,
\[
\begin{eqnarray}
I &=&\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }I_{\mathrm {d}}^{2}\mathrm {d}\theta } \\[ 5pt ]
&=&I_{\mathrm {d}}\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }1\mathrm {d}\theta } \\[ 5pt ]
&=&I_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left[ \theta \right] _{0}^{\frac {2}{3}\pi }} \\[ 5pt ]
&=&I_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left( \frac {2}{3}\pi -0 \right) } \\[ 5pt ]
&=&\sqrt {\frac {2}{3}}I_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
となり,その基本波の実効値\( \ \displaystyle \frac {\sqrt {6}}{\pi }I_{\mathrm {d}} \ \)と比較すると,
\[
\begin{eqnarray}
\frac {\displaystyle \sqrt {\frac {2}{3}}I_{\mathrm {d}}}{\displaystyle \frac {\sqrt {6}}{\pi }I_{\mathrm {d}}} &=&\frac {\pi }{3} \\[ 5pt ]
&≒&1.0472 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 4.7 \ \mathrm {[%]} \ \)程度大きくなります。
(4)解答:ヌ
題意より解答候補は,(ヌ)直流電圧,(カ)交流電源電圧のピーク値,(ヨ)直流電圧の\( \ \displaystyle \frac {1}{2} \ \),になると思います。
ワンポイント解説「2.三相インバータの動作」の通り,二次巻線に加わる電圧は,変換装置の直流電圧を振幅とした\( \ \mathrm {PWM} \ \)波形となります。
(5)解答:チ
題意より解答候補は,(チ)二次電圧又は電流,(リ)交流電力,(ル)一次電圧又は電流,等になると思います。
電圧形自励交直変換装置に用いる変圧器は,変換器が発生する電圧で二次巻線が励磁されるので,スイッチングデバイスのオンオフのタイミングにより,他励用に比べて直流偏磁する可能性が高くなります。そのため,変圧器に偏磁が生じないように直流電圧である二次電圧又は電流を制御すれば良いことになります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん