《機械》〈パワーエレクトロニクス〉[R05:問3]サイリスタを用いた三相整流回路に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，サイリスタを用いた三相整流回路に関する記述である。文中の$\ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

図1のように線間電圧$\ E \ $，角周波数$\ \omega \ $の対称三相交流電源に三相サイリスタ整流回路を接続し，誘導性負荷に直流電流$\ I_{\mathrm {d}} \ $を供給する。図中の$\ L \ $は交流電源側のインダクタンス成分を表す。サイリスタのオン電圧，電源側の抵抗成分，負荷側の電流リプルは無視できるものとする。

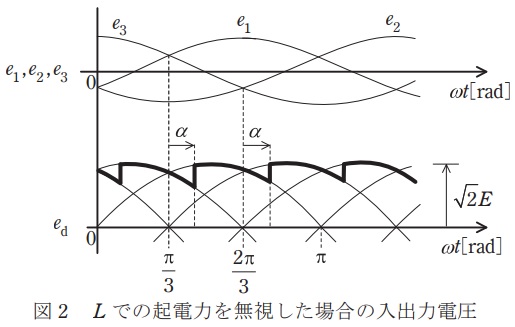
図2は，$\ L \ $での起電力を無視した場合のサイリスタ整流回路の入出力電圧波形である。この場合，ゲート信号を与えたサイリスタはターンオンし，逆バイアスが印加されたサイリスタの電流は直ちに零となりターンオフする。このように電流の流れる経路が変わることを$\ \fbox {　 （１） 　} \ $という。直流電圧$\ e_{\mathrm {d}} \ $は電源の$\ \displaystyle \frac {1}{6} \ $周期ごとに脈動する波形となる。ここで，制御遅れ角（点弧角）を$\ \alpha \ $とすると直流電圧の平均値$\ E_{\mathrm {d}} \ $は，
$$\begin{eqnarray} E_{\mathrm {d}}&=& \ \fbox {　 （２） 　} \ 　・・・・・・・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}$$ で求められる。

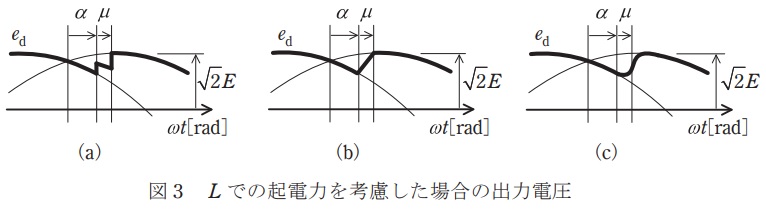
次に，$\ L \ $での起電力を考慮した場合，ゲート信号を与えたサイリスタはターンオンするが，それまでオンしていたサイリスタにも電流が流れ続け，重なり期間$\ \mu \ $が生じる。このときの出力電圧波形は図3$\ \fbox {　 （３） 　} \ $のようになる。図1の回路では電源$\ 1 \ $周期の間に$\ \fbox {　 （４） 　} \ $回の重なり期間が生じる。この場合の直流電圧平均値は①式の$\ E_{\mathrm {d}} \ $$\ \fbox {　 （５） 　} \ $なる。

〔問3の解答群〕
$$\begin{eqnarray} &（イ）&　環流　　　　　&（ロ）&　限流　　　　　&（ハ）&　転流 \\[ 5pt ] &（ニ）&　1　　　　　&（ホ）&　3　　　　　&（ヘ）&　6 \\[ 5pt ] &（ト）&　\frac {3\sqrt {2}}{\pi }E\cos \alpha　　　　　&（チ）&　\frac {3\sqrt {2}}{2\pi }E\cos \alpha　　　　　　　&（リ）&　\frac {3\sqrt {6}}{2\pi }E\cos \alpha \\[ 5pt ] &（ヌ）&　より大きく　　　　　&（ル）&　より小さく　　　　　　&（ヲ）&　と等しく \\[ 5pt ] &（ワ）&　\mathrm {(a)}　　　　　&（カ）&　\mathrm {(b)} 　　　　　&（ヨ）&　\mathrm {(c)} \\[ 5pt ] \end{eqnarray}$$

【ワンポイント解説】

三相サイリスタブリッジ整流回路の動作と出力電圧に関する問題です。
転流における重なり期間を検討しているのが$\ 2 \ $種までにはない内容かと思います。
出力電圧の導出は二次試験対策としては計算で導出できるようになる必要がありますが，計算にも時間を要するので二次試験で選択されない方は暗記しておいても良いでしょう。

1.三相サイリスタブリッジ整流回路の動作と出力電圧
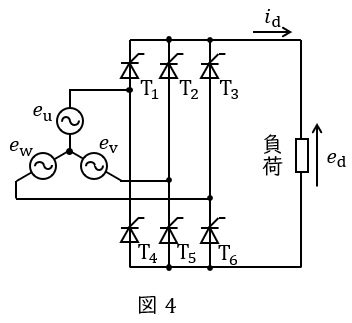
三相サイリスタブリッジ整流回路は図4に示す通り，三相交流回路から$\ 6 \ $つのサイリスタをブリッジ接続して直流を得る回路です。
各サイリスタは制御遅れ角$\ \alpha \ \mathrm {[rad]} \ $で，それぞれオンオフを$\ \displaystyle \frac {2\pi }{3} \ \mathrm {[rad]} \ $ずつ順番に繰り返します。例えば$\ \mathrm {T_{1}} \ $と$\ \mathrm {T_{5}} \ $がオンのときは，$\ e_{\mathrm {u}} \ $→$\ \mathrm {T_{1}} \ $→負荷→$\ \mathrm {T_{5}} \ $→$\ e_{\mathrm {v}} \ $と導通し，出力電圧は$\ e_{\mathrm {u}}-e_{\mathrm {v}} \ $となります。
ここで，電圧$\ e_{\mathrm {u}} \ $を基準とし，
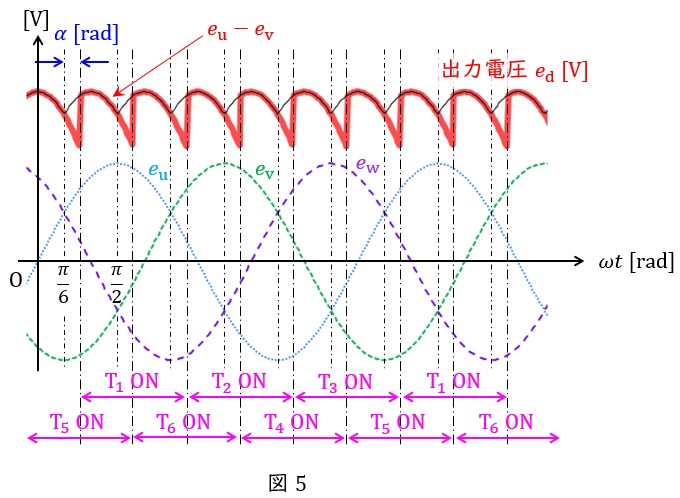
$$\begin{eqnarray} e_{\mathrm {u}}&=& \sqrt {2}E\sin \omega t \\[ 5pt ] e_{\mathrm {v}}&=& \sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ] e_{\mathrm {w}}&=& \sqrt {2}E\sin \left( \omega t-\frac {4}{3}\pi \right) \\[ 5pt ] \end{eqnarray}$$ としたときの出力電圧波形は図5のようになり，出力電圧は$\ \displaystyle \frac {\pi }{3} \ \mathrm {[rad]} \ $毎の繰り返しとなります。したがって，出力電圧の平均値$\ E_{\mathrm {d}} \ \mathrm {[V]} \ $は，
$$\begin{eqnarray} E_{\mathrm {d}}&=& \frac {1}{\displaystyle \frac {\pi }{3}}\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ \sqrt {2}E\sin \omega t-\sqrt {2}E\sin \left( \omega t-\frac {2}{3}\pi \right) \right\}\mathrm {d}\omega t \\[ 5pt ] &=& \frac {3\sqrt {2}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ \sin \omega t-\sin \left( \omega t-\frac {2}{3}\pi \right) \right\}\mathrm {d}\omega t \\[ 5pt ] \end{eqnarray}$$ となります。ここで和積の公式$\ \displaystyle \sin A-\sin B=2\cos \frac {A+B}{2} \sin \frac {A-B}{2} \ $より，
$$\begin{eqnarray} E_{\mathrm {d}}&=& \frac {3\sqrt {2}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ 2\cos \left( \omega t-\frac {\pi }{3}\right) \sin \frac {\pi }{3} \right\}\mathrm {d}\omega t \\[ 5pt ] &=& \frac {3\sqrt {2}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha }\left\{ 2\cos \left( \omega t-\frac {\pi }{3}\right) \cdot \frac {\sqrt {3}}{2} \right\} \mathrm {d}\omega t \\[ 5pt ] &=& \frac {3\sqrt {6}E}{\pi }\int ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha } \cos \left( \omega t-\frac {\pi }{3}\right) \mathrm {d}\omega t \\[ 5pt ] &=& \frac {3\sqrt {6}E}{\pi }\left[ \sin \left( \omega t-\frac {\pi }{3}\right)\right] ^{\frac {\pi }{2}+\alpha }_{\frac {\pi }{6}+\alpha } \\[ 5pt ] &=& \frac {3\sqrt {6}E}{\pi }\left\{ \sin \left( \alpha +\frac {\pi }{6}\right) -\sin \left( \alpha -\frac {\pi }{6}\right)\right\} \\[ 5pt ] &=& \frac {3\sqrt {6}E}{\pi }\cdot 2\cos \alpha \sin \frac {\pi }{6} \\[ 5pt ] &=& \frac {3\sqrt {6}E}{\pi }\cdot 2\cos \alpha \cdot \frac {1}{2} \\[ 5pt ] &=& \frac {3\sqrt {6}E}{\pi }\cos \alpha \\[ 5pt ] \end{eqnarray}$$ と求められます。

【解答】

(1)解答：ハ
題意より解答候補は，（イ）環流，（ロ）限流，（ハ）転流，になると思います。
整流回路において，電流の流れる経路が変わることを転流といいます。

(2)解答：ト
題意より解答候補は，（ト）$\ \displaystyle \frac {3\sqrt {2}}{\pi }E\cos \alpha \ $，（チ）$\ \displaystyle \frac {3\sqrt {2}}{2\pi }E\cos \alpha \ $，（リ）$\ \displaystyle \frac {3\sqrt {6}}{2\pi }E\cos \alpha \ $，になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作と出力電圧」の通り，線間電圧は相電圧の$\ \sqrt {3} \ $倍なので，出力電圧$\ E_{\mathrm {d}} \ $は，$\ E_{\mathrm {d}}=\displaystyle \frac {3\sqrt {2}}{\pi }E\cos \alpha \ $となります。

(3)解答：ワ
題意より解答候補は，（ワ）$\ \mathrm {(a)} \ $，（カ）$\ \mathrm {(b)} \ $，（ヨ）$\ \mathrm {(c)} \ $，になると思います。
転流期間は転流前後の電圧の平均値になるので，波形として正しいのは$\ \mathrm {(a)} \ $となります。

(4)解答：ヘ
題意より解答候補は，（ニ）$\ 1 \ $，（ホ）$\ 3 \ $，（ヘ）$\ 6 \ $，になると思います。
ワンポイント解説「1.三相サイリスタブリッジ整流回路の動作と出力電圧」の通り，図5に示す通り，電源$\ 1 \ $周期の間に$\ 6 \ $回の転流があるため，重なり期間も$\ 6 \ $回発生することになります。

(5)解答：ル
題意より解答候補は，（ヌ）より大きく，（ル）より小さく，（ヲ）と等しく，になると思います。
重なり期間における電圧は理想的な整流回路における電圧よりも小さいので，出力電圧平均値も$\ E_{\mathrm {d}} \ $より小さくなります。