《機械》〈変圧器〉[H21:問2]単相単巻変圧器に関する計算・空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，単相単巻変圧器に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句，式又は数値を解答群の中から選び，その記号をマークシートに記入しなさい。

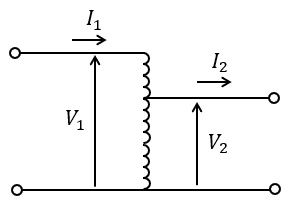
単巻変圧器は，図に示すように一次及び二次巻線の共通な分路巻線と，共通でない直列巻線とから構成される。無負荷時の二次電圧$ \ V_{2} \ $に対する一次電圧$ \ V_{1} \ $の比を$ \ \displaystyle \frac {V_{1}}{V_{2}} \left( V_{1}＞V_{2}\right) \ $とすると，電圧比が$ \ \fbox {　（１）　} \ $ほど分路巻線に流れる電流が小さくなり，同じ負荷容量の二巻線変圧器に比べてサイズが小さく，銅損が少なく，さらに$ \ \fbox {　（２）　} \ $という利点がある。また，単巻変圧器の自己容量は図示した電圧と電流を用いて$ \ \fbox {　（３）　} \ $として表せる。

ここに，容量$ \ 30 \ \mathrm {[kV\cdot A]} \ $の単相二巻線変圧器がある。一次電圧及び二次電圧（負荷側）がそれぞれ$ \ 120 \ \mathrm {[V]} \ $及び$ \ 480 \ \mathrm {[V]} \ $，また，短絡インピーダンスの値が$ \ 8 \ \mathrm {[％]} \ $であるとする。この単相二巻線変圧器の一次巻線を直列巻線に，二次巻線を分路巻線とした単相単巻変圧器を構成すると，原理的にはその単相単巻変圧器の負荷容量は$ \ \fbox {　（４）　} \ \mathrm {[kV\cdot A]} \ $となり，その容量ベースでの短絡インピーダンスの値は$ \ \fbox {　（５）　} \ \mathrm {[％]} \ $となる。ただし，励磁電流は無視するものとする。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　150　　　　　&（ロ）&　4.8　　　　　&（ハ）&　\left( V_{1}-V_{2}\right) I_{1} \\[ 5pt ] &（ニ）&　8　　　　　&（ホ）&　1 \ に近い　　　　　&（ヘ）&　30 \\[ 5pt ] &（ト）&　励磁電流が大きい　　　　　　　&（チ）&　\left( I_{1}-I_{2}\right) V_{1}　　　　　&（リ）&　6 \\[ 5pt ] &（ヌ）&　\sqrt {3} \ に近い　　　　　&（ル）&　電圧変動率が小さい　　　　　　　&（ヲ）&　V_{1}I_{1} \\[ 5pt ] &（ワ）&　1.6　　　　　&（カ）&　\frac {1}{\sqrt {3}} \ に近い　　　　　　&（ヨ）&　絶縁性が良い \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

単相単巻変圧器に関する問題です。
単相単巻変圧器自体は，$ \ 2 \ $種まででも出題されてきたので多くの受験生が理解していると思われますが，本問は出題方法に捻りがあり，しっかりと理解していないと正答が導き出せない問題です。

1.単相単巻変圧器
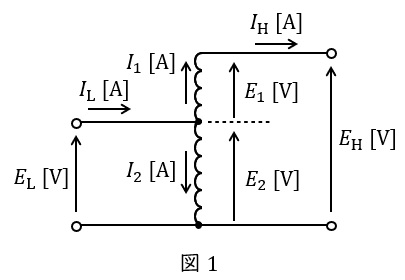
高圧側と低圧側の巻線の一部を共用する変圧器です。共用しない巻線を直列巻線（図1の$ \ E_{1} \ \mathrm {[V]} \ $に当たる巻線），共用する巻線を分路巻線（図1の$ \ E_{2} \ \mathrm {[V]} \ $に当たる巻線）と言います。それぞれの電圧を図1のように定義し，自己容量を$ \ P_{1} \ \mathrm {[V\cdot A]} \ $，分路容量を$ \ P_{2} \ \mathrm {[V\cdot A]} \ $，線路容量を$ \ P_{3} \ \mathrm {[V\cdot A]} \ $とすると，
\[
\begin{eqnarray}
P_{1} &=&E_{1}I_{1} \\[ 5pt ] &=&\left( E_{\mathrm {H}}-E_{\mathrm {L}}\right) I_{\mathrm {H}} \\[ 5pt ] P_{2} &=&E_{2}I_{2} \\[ 5pt ] &=&E_{\mathrm {L}}\left( I_{\mathrm {L}}-I_{\mathrm {H}}\right) \\[ 5pt ] P_{3} &=&E_{\mathrm {L}}I_{\mathrm {L}} \\[ 5pt ] &=&E_{\mathrm {H}}I_{\mathrm {H}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ホ
ワンポイント解説「1.単相単巻変圧器」の通り，分路巻線に流れる電流は$ \ I_{1}-I_{2} \ $であり，$ \ V_{1}I_{1}=V_{2}I_{2} \ $すなわち$ \ \displaystyle \frac {V_{1}}{V_{2}}I_{1}=I_{2} \ $なので，これを代入すると，
\[
\begin{eqnarray}
I_{1}-I_{2} &=&I_{1}-\frac {V_{1}}{V_{2}}I_{1} \\[ 5pt ] &=&\left( 1-\frac {V_{1}}{V_{2}}\right) I_{1} \\[ 5pt ] \end{eqnarray}
\] となり，変圧比が$ \ 1 \ $に近いほど分路巻線に流れる電流は小さくなることがわかります。

(2)解答：ル
題意より解答候補は，（ト）励磁電流が大きい，（ル）電圧変動率が小さい，（ヨ）絶縁性が良い，になると思います。
変圧器の電圧変動率$ \ \varepsilon \ \mathrm {[％]} \ $は，百分率抵抗降下を$ \ p \ \mathrm {[％]} \ $，百分率リアクタンス降下を$ \ q \ \mathrm {[％]} \ $，負荷の力率を$ \ \cos \theta \ $とすると，
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta +q\sin \theta \\[ 5pt ] \end{eqnarray}
\] であるため，二巻線変圧器に比べてインピーダンスを小さくできる単巻変圧器は電圧変動率が小さいという特徴があります。

(3)解答：ハ
題意より解答候補は，（ハ）$ \ \left( V_{1}-V_{2}\right) I_{1} \ $，（チ）$ \ \left( I_{1}-I_{2}\right) V_{1} \ $，（ヲ）$ \ V_{1}I_{1} \ $，になると思います。
ワンポイント解説「1.単相単巻変圧器」の通り，自己容量は$ \ \left( V_{1}-V_{2}\right) I_{1} \ $となります。

(4)解答：イ
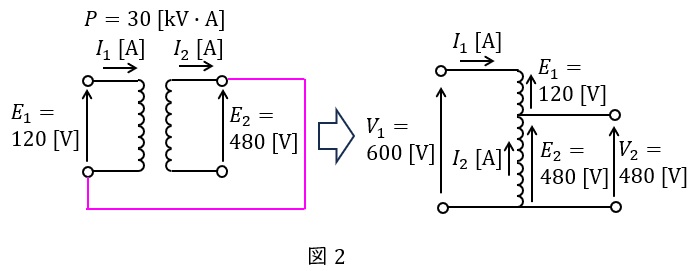
容量$ \ P=30 \ \mathrm {[kV\cdot A]} \ $，一次電圧$ \ E_{1}=120 \ \mathrm {[V]} \ $，二次電圧$ \ E_{2}=480 \ \mathrm {[V]} \ $の単相二巻線変圧器は図2のように接続することで，単相単巻変圧器を構成できる。
図2より，一次電流$ \ I_{1} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I_{1}&=&\frac {P}{E_{1}} \\[ 5pt ] &=&\frac {30\times 10^{3}}{120} \\[ 5pt ] &=&250 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] なので，単巻変圧器の負荷容量$ \ P_{l} \ \mathrm {[kV\cdot A]} \ $は，
\[
\begin{eqnarray}
P_{l}&=&V_{1}I_{1} \\[ 5pt ] &=&600\times 250 \\[ 5pt ] &=&150 \ 000 \ \mathrm {[V\cdot A]}　→　150 \ \mathrm {[kV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ワ
容量$ \ P=30 \ \mathrm {[kV\cdot A]} \ $，一次電圧$ \ E_{1}=120 \ \mathrm {[V]} \ $，一次電流$ \ I_{1}=250 \ \mathrm {[A]} \ $での短絡インピーダンス$ \ ％Z=8 \ \mathrm {[％]} \ $なので，百分率インピーダンスの定義式よりそのインピーダンス$ \ Z \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{1}}{E_{1}}\times 100 \\[ 5pt ] Z&=&\frac {E_{1}％Z}{100I_{1}} \\[ 5pt ] &=&\frac {120\times 8}{100\times 250} \\[ 5pt ] &=&0.0384 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。$ \ Z=0.0384 \ \mathrm {[\Omega ]} \ $について，一次電圧$ \ V_{1}=600 \ \mathrm {[V]} \ $，一次電流$ \ I_{1}=250 \ \mathrm {[A]} \ $での短絡インピーダンス$ \ ％Z^{\prime } \ \mathrm {[％]} \ $を求めると，
\[
\begin{eqnarray}
％Z^{\prime }&=&\frac {ZI_{1}}{V_{1}}\times 100 \\[ 5pt ] &=&\frac {0.0384\times 250}{600}\times 100 \\[ 5pt ] &=&1.6 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

※容量比較で解いても良いですが，変圧器の並行運転時の容量換算とは異なることに注意して下さい。