【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,図1に示す三相ブリッジ接続の電圧形自励インバータに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
このインバータの交流出力端子\( \ \mathrm {U} \ \),\( \ \mathrm {V} \ \),\( \ \mathrm {W} \ \)は,インバータ容量を基準として\( \ 10 \ % \ \)程度のリアクタンスをもつリアクトル\( \ \mathrm {X} \ \)を介して一定電圧・一定周波数の三相交流電源\( \ \mathrm {E} \ \)に接続されている。出力電圧は,パルス幅変調制御によって制御されている。パルス幅変調制御は,例えば\( \ \mathrm {U} \ \)相では,図2に示すように\( \ \mathrm {U} \ \)相の正弦波の信号波\( \ v_{\mathrm {S}} \ \)を三角波の搬送波\( \ v_{\mathrm {C}} \ \)と比較して行われている。
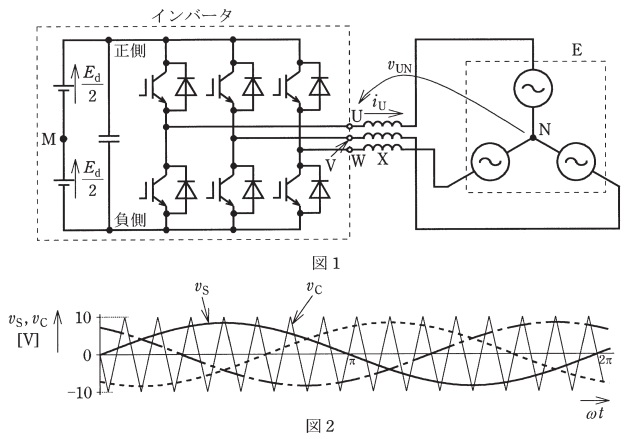
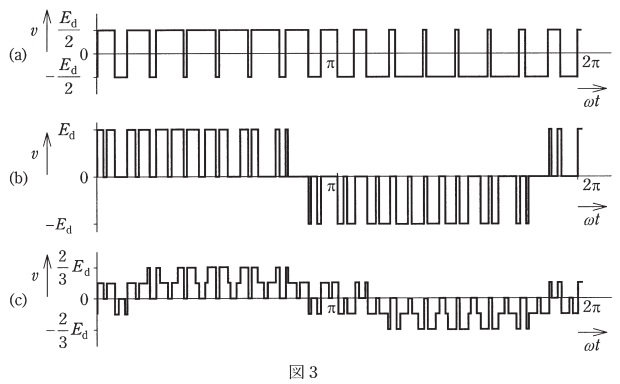
直流電圧\( \ E_{\mathrm {d}} \ \)が\( \ 330 \ \mathrm {V} \ \),\( \ v_{\mathrm {C}} \ \)の振幅が\( \ 10 \ \mathrm {V} \ \),\( \ v_{\mathrm {S}} \ \)の振幅が\( \ 9 \ \mathrm {V} \ \)のとき,出力端子における線間交流電圧の基本波実効値は\( \ \fbox { (1) } \ \mathrm {V} \ \)である。\( \ v_{\mathrm {C}} \ \)の周波数は,\( \ v_{\mathrm {S}} \ \)の周波数の\( \ 15 \ \)倍としている。線間交流電圧には主として\( \ \fbox { (2) } \ \)の高調波電圧を生じる。図3は,このインバータ各部の電圧波形である。この内,三相交流電源\( \ \mathrm {E} \ \)の中点\( \ \mathrm {N} \ \)に対する\( \ \mathrm {U} \ \)相端子電圧\( \ v_{\mathrm {UN}} \ \)の波形は,図の\( \ \fbox { (3) } \ \)である。
このインバータで交流電源における基本波力率が\( \ 1 \ \)になるようにして基本波交流電流の大きさを変えたとき,基本波電圧の振幅は\( \ \fbox { (4) } \ \)。
各相の正側のアームの\( \ \mathrm {IGBT} \ \)をオフして負側のアームの\( \ \mathrm {IGBT} \ \)をオンするとき,又はその逆に負側をオフして正側をオンするとき,実際には直流短絡を防止するためにオフからオンまでの間にデッドタイムを設ける。デッドタイムの期間の仮想直流中点\( \ \mathrm {M} \ \)に対する当該相の出力電圧は,交流電流が負の状態(インバータに流れ込む方向)のときは,\( \ \fbox { (5) } \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& 210 &(ロ)& \mathrm {(b)} &(ハ)& 14次・16次 \\[ 5pt ]
&(ニ)& \mathrm {(c)} &(ホ)& 242 &(ヘ)& 0 \\[ 5pt ]
&(ト)& 13 \ 次・17 \ 次 &(チ)& 182 &(リ)& \frac {E_{\mathrm {d}}}{2} \\[ 5pt ]
&(ヌ)& 15 \ 次・30 \ 次 &(ル)& -\frac {E_{\mathrm {d}}}{2} &(ヲ)& \mathrm {(a)} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ワ)& 基本波電流の大きさの平方根に比例して変わる \\[ 5pt ]
&(カ)& 基本波電流の大きさに比例して変わる \\[ 5pt ]
&(ヨ)& あまり変わらない \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相ブリッジ接続の電圧形自励インバータに関する問題です。かなり複雑な問題ですが,一種で新たに必要となるような公式はありません。波形をよーくイメージしながら,解くようにして下さい。
【関連する「電気の神髄」記事】
【解答】
(1)解答:チ
図2における単相分の出力は\( \ \displaystyle \frac {T_{\mathrm {on}}}{T}E_{\mathrm {d}} \ \)であり,
\[
\frac {T_{\mathrm {on}}}{T}=\frac {9\sin \omega t}{10}
\]
であるから,線間交流電圧の基本波実効値\( \ V \ \)は,
\[
\begin{eqnarray}
V&=& \frac {\displaystyle \frac {9}{\sqrt {2}}}{10}\frac {E_{\mathrm {d}}}{2}\cdot \sqrt {3} \\[ 5pt ]
&=& \frac {\displaystyle \frac {9}{\sqrt {2}}}{10}\frac {330}{2}\cdot \sqrt {3} \\[ 5pt ]
&≒& 182 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
(2)解答:ト
図2において\( \ v_{\mathrm {C}} \ \)の周波数が\( \ v_{\mathrm {S}} \ \)の\( \ 15 \ \)倍であるので,\( \ 15 \ \)に近い次数の高調波が発生する。また,出力は\( \ \pi \ \)を基準とした奇関数となるので,発生する高調波は奇数次の高調波となる。よって,\( \ 13 \ \)次・\( \ 17 \ \)次の高調波が主として生じる。
(3)解答:ニ
\( \ \mathrm {M} \ \)を基準とした,\( \ \mathrm {U} \ \),\( \ \mathrm {V} \ \),\( \ \mathrm {W} \ \),\( \ \mathrm {N} \ \)の電位をそれぞれ\( \ E_{\mathrm {U}} \ \),\( \ E_{\mathrm {V}} \ \),\( \ E_{\mathrm {W}} \ \),\( \ E_{\mathrm {N}} \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}}& ・・・・・①& \\[ 5pt ]
v_{\mathrm {VN}}&=& E_{\mathrm {V}}-E_{\mathrm {N}}& ・・・・・②& \\[ 5pt ]
v_{\mathrm {WN}}&=& E_{\mathrm {W}}-E_{\mathrm {N}}& ・・・・・③& \\[ 5pt ]
v_{\mathrm {UN}}+v_{\mathrm {VN}}+v_{\mathrm {WN}}&=&0& ・・・・・④&
\end{eqnarray}
\]
①~③を④に代入して整理すると,
\[
\begin{eqnarray}
E_{\mathrm {U}}-E_{\mathrm {N}}+E_{\mathrm {V}}-E_{\mathrm {N}}+E_{\mathrm {W}}-E_{\mathrm {N}}&=&0 \\[ 5pt ]
E_{\mathrm {N}}&=&\frac {E_{\mathrm {U}}+E_{\mathrm {V}}+E_{\mathrm {W}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,各値が取りうる値を求めると,
①\( \ \displaystyle E_{\mathrm {U}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle \frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2} \\[ 5pt ]
&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \displaystyle E_{\mathrm {U}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle \frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
③\( \ \displaystyle E_{\mathrm {U}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=-\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle \frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
④\( \ \displaystyle E_{\mathrm {U}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=-\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle \frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&-\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& \frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
&=& \frac {2E_{\mathrm {d}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
⑤\( \ \displaystyle E_{\mathrm {U}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle -\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& -\frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
&=& -\frac {2E_{\mathrm {d}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
⑥\( \ \displaystyle E_{\mathrm {U}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle -\frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&-\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& -\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
&=& -\frac {E_{\mathrm {d}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
⑦\( \ \displaystyle E_{\mathrm {U}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=-\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle -\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&-\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& -\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{6} \\[ 5pt ]
&=& -\frac {E_{\mathrm {d}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
⑧\( \ \displaystyle E_{\mathrm {U}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {V}}=-\frac {E_{\mathrm {d}}}{2} \ \),\( \ \displaystyle E_{\mathrm {W}}=-\frac {E_{\mathrm {d}}}{2} \ \)の時
\[
\begin{eqnarray}
E_{\mathrm {N}}&=&\frac {\displaystyle \frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}-\frac {E_{\mathrm {d}}}{2}}{3} \\[ 5pt ]
&=&-\frac {E_{\mathrm {d}}}{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {UN}}&=& E_{\mathrm {U}}-E_{\mathrm {N}} \\[ 5pt ]
&=& -\frac {E_{\mathrm {d}}}{2}+\frac {E_{\mathrm {d}}}{2} \\[ 5pt ]
&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ v_{\mathrm {UN}} \ \)の取りうる値は,\( \ \displaystyle \frac {2E_{\mathrm {d}}}{3} \ \),\( \ \displaystyle \frac {E_{\mathrm {d}}}{3} \ \),\( \ 0 \ \),\( \ \displaystyle -\frac {E_{\mathrm {d}}}{3} \ \),\( \ \displaystyle -\frac {2E_{\mathrm {d}}}{3} \ \)となるので,グラフは\( \ \mathrm {(c)} \ \)となる。
(4)解答:ヨ
基本波電圧は基本波交流電流に依存しないと考えられるので,基本波電流を変えても基本波電圧はあまり変わらない。
(5)解答:リ
交流電流が負の時,デッドタイム中は正側の\( \ \mathrm{IGBT} \ \)が導通するので,出力電圧は\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん