【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,同期発電機の出力に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は式を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
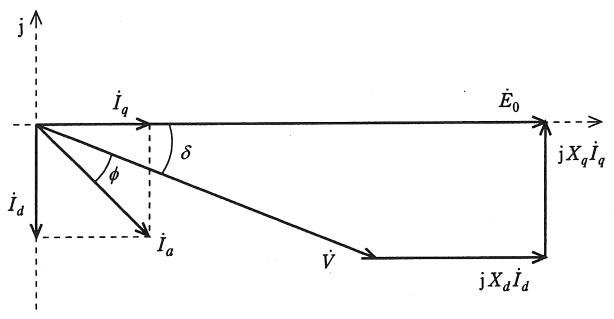
図は,遅れ力率で運転されている三相突極形同期発電機の一相分のベクトル図(フェーザ図)である。ただし,\( \ \dot V \ \)は端子電圧(相電圧),\( \ \dot E_{0} \ \)は無負荷誘導起電力(相電圧),\( \ {\dot I}_{a} \ \)は電機子電流,\( \ {\dot I}_{d} \ \)は\( \ {\dot I}_{a} \ \)の直軸分,\( \ {\dot I}_{q} \ \)は\( \ {\dot I}_{a} \ \)の横軸分,\( \ X_{d} \ \)は直軸同期リアクタンス,\( \ X_{q} \ \)は横軸同期リアクタンス,\( \ \fbox { (1) } \ \)は負荷角,\( \ \phi \ \)は力率角とし,また,電機子抵抗は無視するものとする。
\( \ \dot E_{0} \ \)を基準ベクトルとすると,ベクトル図から,\( \ \dot E_{0}=E_{0} \ \),\( \ {\dot I}_{a}= \ \fbox { (2) } \ \),\( \ \dot V=V\mathrm {e}^{-\mathrm {j}\delta } \ \)となるから,出力は
\[
\begin{eqnarray}
P &=&\mathrm {Re}\left( 3\overline {\dot V} {\dot I}_{a}\right) = \ \fbox { (3) } \ ・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ I_{d} \ \),\( \ I_{q} \ \)を求めるため,ベクトル図から,
\[
\begin{eqnarray}
V \cos \delta &=&E_{0}-X_{d}I_{d} & \ ・・・・・・・・・・・・・・・・・・・ ②& \\[ 5pt ]
V \sin \delta &=&X_{q}I_{q} & \ ・・・・・・・・・・・・・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
なる関係を得る。これを①式に代入して整理すると,
\[
\begin{eqnarray}
P&=&3\frac {VE_{0}}{X_{d}}\sin \delta +\frac {3}{2}\left( \frac {1}{X_{q}}-\frac {1}{X_{d}}\right) V^{2}\times \ \fbox { (4) } \ &・・・・・・・ ④& \\[ 5pt ]
\end{eqnarray}
\]
となる。一般に\( \ \delta \ \)が\( \ 60 \ \mathrm {[°]}~70 \ \mathrm {[°]} \ \)のときに突極形発電機の出力は最大となる。
非突極機では,\( \ X_{d}=X_{q} \ \)といえるから,これを\( \ X_{s} \ \)とおくと出力は,
\[
\begin{eqnarray}
P&=&3\frac {VE_{0}}{X_{s}}\sin \delta & \ ・・・・・・・・・・・・・・・・・・・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
となり,非突極機の出力は\( \ \delta \ \)が\( \ 90 \ \mathrm {[°]} \ \)で最大となる。
突極機の場合,界磁電流の大きさに依存しない④式第二項が存在する。これは\( \ \fbox { (5) } \ \)に基づくもので,突極機に特有なものである。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& I_{d}-\mathrm {j}I_{q} &(ロ)& 反作用トルク &(ハ)& \delta -\phi \\[ 5pt ]
&(ニ)& \delta +\phi &(ホ)& I_{q}+\mathrm {j}I_{d} &(ヘ)& 3V\left( I_{q}\cos \delta +I_{d}\sin \delta \right) \\[ 5pt ]
&(ト)& I_{q}-\mathrm {j}I_{d} &(チ)& 作用トルク &(リ)& \cos \delta \\[ 5pt ]
&(ヌ)& 3V\left( I_{q}+I_{d}\right) \sin \delta &(ル)& \sin 2\delta &(ヲ)& 負荷トルク \\[ 5pt ]
&(ワ)& \cos 2\delta &(カ)& \delta &(ヨ)& 3V\left( I_{d}\cos \delta +I_{q}\sin \delta \right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
突極形同期発電機の出力の導出に関する問題ですが,実質的には問題文に沿って演算ができるかどうかの数学力が問われています。
突極形同期発電機は\( \ 2 \ \)種まではあまり出題されないですが,\( \ 1 \ \)種では比較的高い頻度で出題されますので,理解しておくようにしましょう。
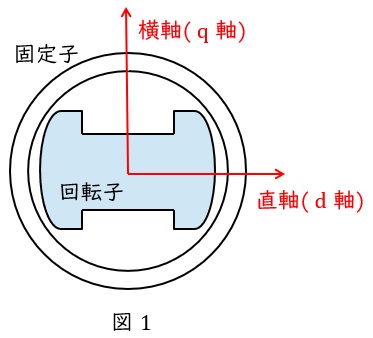
1.突極形同期発電機の構造及びベクトル図
突極形同期発電機の構造は図1のようになり,回転子の磁極と同じ向きの軸を直軸(\( \ \mathrm {d} \ \)軸),磁極と直角の向きの軸を横軸(\( \ \mathrm {q} \ \)軸)といいます。
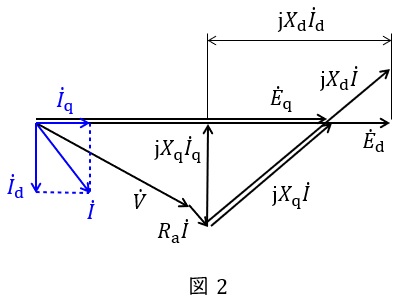
円筒機は直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)と横軸同期リアクタンス\( \ X_{\mathrm {q}} \ \)がほぼ等しいので,基本的な同期発電機の等価回路やベクトル図が適用できますが,突極機の場合はその構造上\( \ X_{\mathrm {d}}>X_{\mathrm {q}} \ \)となるので,ベクトル図としては図2のようになります。
図2において,\( \ {\dot E}_{\mathrm {d}} \ \):無負荷誘導起電力,\( \ {\dot E}_{\mathrm {q}} \ \):内部横軸リアクタンス電圧,\( \ \dot I \ \):電機子電流,\( \ {\dot I}_{\mathrm {d}} \ \):電機子電流の直軸分,\( \ {\dot I}_{\mathrm {q}} \ \):電機子電流の横軸分,\( \ R_{\mathrm {a}} \ \):電機子抵抗(無視することも多い),となります。
2.突極形同期発電機の直軸同期リアクタンスと横軸同期リアクタンスの違い
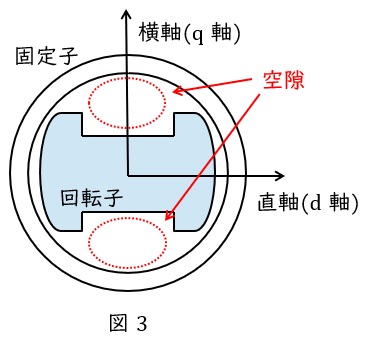
円筒形同期発電機は直軸方向と横軸方向の透磁率の違いはほとんどありませんが,突極形同期発電機は図3に示すように,横軸方向に空隙がある分横軸方向の方が透磁率は小さくなります。
透磁率が小さいと磁気抵抗\( \ \displaystyle R_{\mathrm {m}}\left( =\frac {l}{\mu S}\right) \ \)が大きくなります。
磁気抵抗\( \ \displaystyle R_{\mathrm {m}} \ \)が大きいと,インダクタンス\( \ \displaystyle L\left( =\frac {N^{2}}{R_{\mathrm {m}}}\right) \ \)は小さくなります。
よって,突極形同期発電機においては直軸同期リアクタンス\( \ X_{\mathrm {d}} \ \)の方が横軸同期リアクタンス \( \ X_{\mathrm {q}} \ \)より大きくなります。
【解答】
(1)解答:カ
題意より解答候補は,(ハ)\( \ \delta -\phi \ \),(ニ)\( \ \delta +\phi \ \),(カ)\( \ \delta \ \),になると思います。
一般に負荷角は端子電圧\( \ \dot V \ \)と無負荷誘導起電力\( \ \dot E_{0} \ \)の位相差を言い,問題図においては\( \ \delta \ \)となります。
(2)解答:ト
題意より解答候補は,(イ)\( \ I_{d}-\mathrm {j}I_{q} \ \),(ホ)\( \ I_{q}+\mathrm {j}I_{d} \ \),(ト)\( \ I_{q}-\mathrm {j}I_{d} \ \),になると思います。
問題図より,\( \ {\dot I}_{a}=I_{q}-\mathrm {j}I_{d} \ \)となります。
(3)解答:ヘ
題意より,複素電力\( \ \dot S \ \)は,
\[
\begin{eqnarray}
\dot S &=&3\overline {\dot V} {\dot I}_{a} \\[ 5pt ]
&=&3V\mathrm {e}^{\mathrm {j}\delta }\left( I_{q}-\mathrm {j}I_{d}\right) \\[ 5pt ]
&=&3V\left( \cos \delta +\mathrm {j}\sin \delta \right) \left( I_{q}-\mathrm {j}I_{d}\right) \\[ 5pt ]
&=&3V\left( I_{q}\cos \delta -\mathrm {j}I_{d}\cos \delta +\mathrm {j}I_{q}\sin \delta +I_{d}\sin \delta \right) \\[ 5pt ]
&=&3V\left\{ I_{q}\cos \delta +I_{d}\sin \delta +\mathrm {j}\left( I_{q}\sin \delta -I_{d}\cos \delta\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,出力\( \ P \ \)は,
\[
\begin{eqnarray}
P &=&\mathrm {Re}\left( 3\overline {\dot V} {\dot I}_{a}\right) \\[ 5pt ]
&=&3V\left( I_{q}\cos \delta +I_{d}\sin \delta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
②及び③より,
\[
\begin{eqnarray}
V \cos \delta &=&E_{0}-X_{d}I_{d} \\[ 5pt ]
X_{d}I_{d} &=&E_{0}-V \cos \delta \\[ 5pt ]
I_{d} &=&\frac {E_{0}-V \cos \delta }{X_{d}} \\[ 5pt ]
V \sin \delta &=&X_{q}I_{q} \\[ 5pt ]
I_{q}&=&\frac {V \sin \delta }{X_{q}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを(3)解答式に代入すると,
\[
\begin{eqnarray}
P &=&3V\left( I_{q}\cos \delta +I_{d}\sin \delta \right) \\[ 5pt ]
&=&3V\left( \frac {V \sin \delta }{X_{q}}\cos \delta +\frac {E_{0}-V \cos \delta }{X_{d}}\sin \delta \right) \\[ 5pt ]
&=&\frac {3V^{2} \sin \delta \cos \delta }{X_{q}}+\frac {3VE_{0}\sin \delta -3V^{2} \sin \delta \cos \delta }{X_{d}} \\[ 5pt ]
&=&\frac {3VE_{0}}{X_{d}}\sin \delta +\frac {3V^{2} \sin \delta \cos \delta }{X_{q}}-\frac {3V^{2} \sin \delta \cos \delta }{X_{d}} \\[ 5pt ]
&=&\frac {3VE_{0}}{X_{d}}\sin \delta +3\left( \frac {1}{X_{q}}-\frac {1}{X_{d}}\right) V^{2} \sin \delta \cos \delta \\[ 5pt ]
&=&\frac {3VE_{0}}{X_{d}}\sin \delta +3\left( \frac {1}{X_{q}}-\frac {1}{X_{d}}\right) V^{2} \frac {\sin 2\delta }{2} \\[ 5pt ]
&=&3\frac {VE_{0}}{X_{d}}\sin \delta +\frac {3}{2}\left( \frac {1}{X_{q}}-\frac {1}{X_{d}}\right) V^{2}\times \sin 2\delta \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ロ
題意より解答候補は,(ロ)反作用トルク,(チ)作用トルク,(ヲ)負荷トルク,になると思います。
突極機にはその構造から反作用トルクというトルクが働き,④式の第二項は反作用トルクに基づくものとなります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん