《機械》〈照明〉[R06:問4]光源の全光束の求め方に関する計算・空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，光源の全光束の求め方に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

配光は，光源が放射する光束を，$ \ \fbox {　（１）　} \ $の空間分布として表したものである。鉛直配光が水平角$ \ \varphi \ $に依存しない場合は，配光は鉛直角$ \ \theta \ $の関数$ \ I\left( \theta \right) \ $として表される。このとき，この光源の全光束$ \ \mathit {\Phi } \ $は次式によって表される。
\[
\begin{eqnarray}
\mathit {\Phi } &=& \ \fbox {　（２）　} \ 　・・・・・・・・・・・・・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] 実在の光源では複雑な配光を有するものが多いので，全光束$ \ \mathit {\Phi } \ $は実測した$ \ I\left( \theta \right) \ $を数値積分することで求める。その方法の一つとして，以下に示す$ \ \fbox {　（３）　} \ $と呼ばれる図を用いる方法がある。

$ \ \fbox {　（３）　} \ $の左側には，光源の光中心を中心とした半径$ \ r \ $の半円を描き，その内側に配光$ \ I\left( \theta \right) \ $（曲線$ \ \mathrm {abc} \ $）を描く。また，半円上において，$ \ \theta \ $に対応する点を$ \ \mathrm {P} \ $としている。

さらに，図の右側には，直交座標$ \ xy \ $をとっている。$ \ x \ $軸（縦軸）において，座標の原点$ \ \mathrm {O} \ $は，左側の半円上の$ \ \theta =0 \ $の点$ \ \mathrm {N} \ $に対応している。同様に，$ \ x \ $軸上の点$ \ \mathrm {P}^{\prime } \ $は半円上の点$ \ \mathrm {P} \ $に対応している。$ \ x \ $軸において，原点$ \ \mathrm {O} \ $から点$ \ \mathrm {P}^{\prime } \ $までの長さ（点$ \ \mathrm {P} \ $における球帽の高さ）が$ \ x \ $である。$ \ y \ $軸（横軸）には，$ \ \theta \ $に対応する$ \ I\left( \theta \right) \ $をプロットしている。すなわち，図の左側の配光曲線$ \ \mathrm {abc} \ $が，図の右側の曲線$ \ \mathrm {ABC} \ $に対応している。

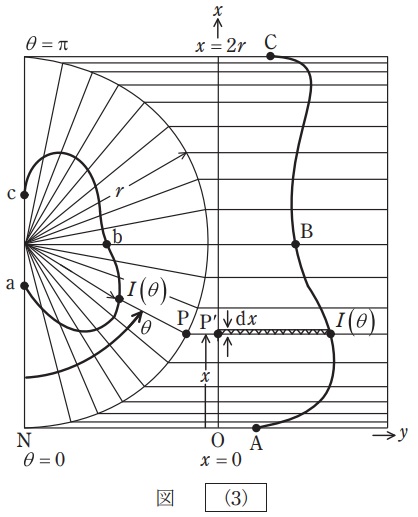
この図において，$ \ x \ $軸上の微小幅を$ \ \mathrm {d}x \ $とすると，曲線$ \ \mathrm {ABC} \ $と$ \ x \ $軸とで囲まれる面の面積$ \ S \ $は次式で与えられる。
\[
\begin{eqnarray}
S &=& \int _{0}^{2r} I\left( \theta \right) \mathrm {d}x 　・・・・・・・・・・・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] ここで，$ \ x \ $は$ \ r \ $と$ \ \theta \ $を使って
\[
\begin{eqnarray}
x &=& r\left( 1-\cos \theta \right) \ 　・・・・・・・・・・・・・・・・・・・・　③ \\[ 5pt ] \end{eqnarray}
\] と表すことができるので，これを使うと，②式は次式のようになる。
\[
\begin{eqnarray}
S &=& \ \fbox {　（４）　} 　・・・・・・・・・・・・・・・・・・・・・・　④ \\[ 5pt ] \end{eqnarray}
\] さらに，①式と④式とを比較することで次式を求めることができる。
\[
\begin{eqnarray}
\mathit {\Phi } &=& \ \fbox {　（５）　} 　・・・・・・・・・・・・・・・・・・・・・・　⑤ \\[ 5pt ] \end{eqnarray}
\] すなわち，面積$ \ S \ $を求めることによって，光源の全光束$ \ \mathit {\Phi } \ $を求めることができる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　2r\int _{0}^{\pi }I\left( \theta \right) \cos \theta \mathrm {d}\theta 　　　　　&（ロ）&　2\pi \int _{0}^{\pi }I\left( \theta \right) \cos \theta \mathrm {d}\theta 　　　　　&（ハ）&　2\pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ] &（ニ）&　\frac {\pi }{r}S 　　　　　&（ホ）&　\frac {2\pi }{r}S 　　　　　&（ヘ）&　\frac {\pi }{2r}S \\[ 5pt ] &（ト）&　ルーソー図　　　　　&（チ）&　色度図　　　　　&（リ）&　等光度図 \\[ 5pt ] &（ヌ）&　輝度　　　　　&（ル）&　光度　　　　　&（ヲ）&　光束発散度 \\[ 5pt ] &（ワ）&　\pi \int _{0}^{\pi }I\left( \theta \right) \mathrm {d}\theta 　　　　　&（カ）&　r \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta 　　　　　&（ヨ）&　2r \int _{0}^{\pi }I\left( \theta \right) \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

光源の配光と全光束を求める方法に関する問題です。
均等放射の光源に関する問題が電験では出題されるので，本問は少し専門領域に入る部類の内容かと思います。
知識以上に文章を読解しながら解いていく数学力が問われている$ \ 1 \ $種らしい問題です。

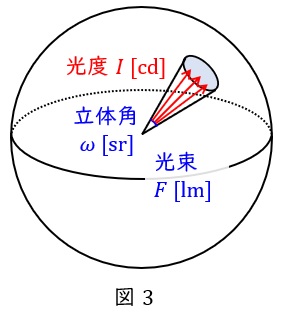
1.光束$ \ F \ $
光源から出る可視光の量（エネルギー）で，単位は$ \ \mathrm {[lm]} \ $となります。
電磁気の分野の電束に似たようなイメージで良いです。

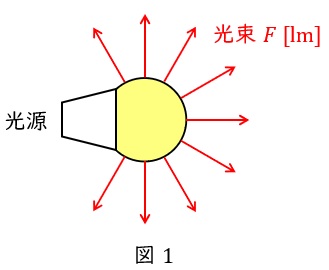
2.立体角の定義
図2のように球体があり，半径$ \ r \ \mathrm {[m]} \ $の錐体が球面を切り取った時の面積を$ \ S \ \mathrm {[m^{2}]} \ $とすると，立体角$ \ \omega \ \mathrm {[sr]} \ $は，
\[
\begin{eqnarray}
\omega &=&\frac {S}{r^{2}} \\[ 5pt ] \end{eqnarray}
\] であり，平面角$ \ \theta \ \mathrm {[rad]} \ $で表すと，
\[
\begin{eqnarray}
\omega &=&2\pi \left( 1-\cos \theta \right) \\[ 5pt ] \end{eqnarray}
\] となります。球全体の立体角は$ \ \theta = \pi \ $の時であり，$ \ \omega =4\pi \ $となります。

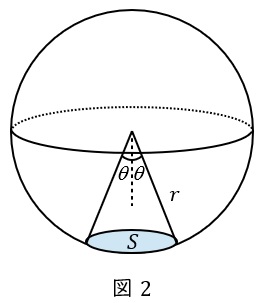
3.光度$ \ I \ $
ある方向に向かう光束を立体角で割ったもので，微小立体角$ \ \mathrm {d}\omega \ \mathrm {[sr]} \ $に向かう光束が$ \ \mathrm {d}F \ \mathrm {[lm]} \ $であるとき，光度$ \ I \ \mathrm {[cd]} \ $は，
\[
\begin{eqnarray}
I &=&\frac {\mathrm {d}F}{\mathrm {d}\omega } \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ル
題意より解答候補は，（ヌ）輝度，（ル）光度，（ヲ）光束発散度，になると思います。
ワンポイント解説「1.光束$ \ F \ $」や「3.光度$ \ I \ $」の通り，配光は光源が放射する光束を，光度の空間分布として表したものとなります。輝度や光束発散度を忘れてしまった方は令和3年問5の問題を見てみて下さい。

(2)解答：ハ
ワンポイント解説「3.光度$ \ I \ $」の通り，
\[
\begin{eqnarray}
I &=&\frac {\mathrm {d}\mathit {\Phi }}{\mathrm {d}\omega } \\[ 5pt ] \mathrm {d}\mathit {\Phi }&=&I\mathrm {d}\omega \\[ 5pt ] \end{eqnarray}
\] の関係があり，ワンポイント解説「2.立体角の定義」より，
\[
\begin{eqnarray}
\frac {\mathrm {d}\omega }{\mathrm {d}\theta } &=&\left\{ 2\pi \left( 1-\cos \theta \right)\right\} ^{\prime } \\[ 5pt ] &=&2\pi \sin \theta \\[ 5pt ] \mathrm {d}\omega &=&2\pi \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
\mathrm {d}\mathit {\Phi }&=&I\mathrm {d}\omega \\[ 5pt ] &=&2\pi I\sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] となる。よって，全光束$ \ \mathit {\Phi } \ $は$ \ \theta \ $を$ \ 0 \ $から$ \ \pi \ $まで積分したものであるから，
\[
\begin{eqnarray}
\mathit {\Phi } &=& 2\pi \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
題意より解答候補は，（ト）ルーソー図，（チ）色度図，（リ）等光度図，になると思います。
問題に与えられている図をルーソー図といいます。専門用語ですから，本空欄は覚えておくしかありません。

(4)解答：カ
③式の両辺を微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}x }{\mathrm {d}\theta } &=& r\sin \theta \\[ 5pt ] \mathrm {d}x &=& r\sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] であり，$ \ x \ $が$ \ 0 \ $から$ \ 2r \ $まで変化するとき，$ \ \theta \ $は$ \ 0 \ $から$ \ \pi \ $まで変化するので，②式は，
\[
\begin{eqnarray}
S &=&r \int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
(4)解答式より，
\[
\begin{eqnarray}
\int _{0}^{\pi }I\left( \theta \right) \sin \theta \mathrm {d}\theta &=&\frac {S}{r} \\[ 5pt ] \end{eqnarray}
\] であるから，これを(2)解答式に代入すると，
\[
\begin{eqnarray}
\mathit {\Phi } &=& 2\pi \cdot \frac {S}{r} \\[ 5pt ] &=& \frac {2\pi }{r}S \\[ 5pt ] \end{eqnarray}
\] と求められる。