【問題】
【難易度】★★★★☆(やや難しい)
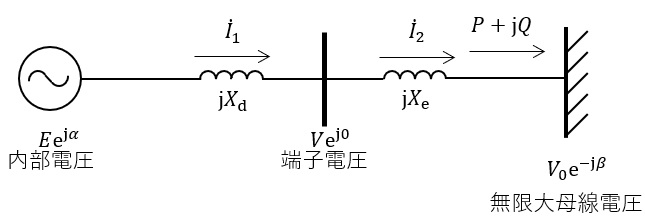
図に示す\( \ 1 \ \)機無限大母線系統において,発電所から無限大母線へと送電することを考える。発電機の内部電圧と端子電圧をそれぞれ\( \ E\mathrm {e}^{\mathrm {j}\alpha } \ \)及び\( \ V\mathrm {e}^{\mathrm {j}0 } \ \),無限大母線の電圧を\( \ V_{0}\mathrm {e}^{-\mathrm {j}\beta } \ \),発電機の同期リアクタンスを\( \ X_{\mathrm {d}} \ \),送電線のリアクタンスを\( \ X_{\mathrm {e}} \ \)とする(ただし,\( \ \alpha > 0 \ \),\( \ \beta > 0 \ \)とする)。無限大母線での受電電力を\( \ P+\mathrm {j}Q \ \)とする(ただし\( \ P > 0 \ \)。\( \ Q \ \)は遅れを正とする)。送電線の抵抗や静電容量は無視して良い。全ての変数は共通の基準値による単位法表現とし,以下の問に答えよ。なお,同期化力が\( \ 0 \ \)以上である場合には小じょう乱同期安定性(定態安定度)の観点から安定な送電は可能とする。
(1) 無限大母線の受電電力\( \ P \ \)及び\( \ Q \ \)を,それぞれ\( \ E \ \),\( \ V_{0} \ \),\( \ \alpha \ \),\( \ \beta \ \),\( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {e}} \ \)を用いて表せ。
(2) 同期化力により定まる小じょう乱同期安定性の観点から,安定な送電のために\( \ \alpha + \beta \ \)が満たすべき条件を示せ。
(3) 図の\( \ \mathrm {j}X_{\mathrm {d}} \ \)を流れる電流\( \ {\dot I}_{1} \ \)を,\( \ E \ \),\( \ V \ \),\( \ \alpha \ \),\( \ X_{\mathrm {d}} \ \)を用いて表せ。同様に,\( \ \mathrm {j}X_{\mathrm {e}} \ \)を流れる電流\( \ {\dot I}_{2} \ \)を,\( \ V \ \),\( \ V_{0} \ \),\( \ \beta \ \),\( \ X_{\mathrm {e}} \ \)を用いて表せ。
(4) 小問(2)で示した小じょう乱同期安定限界において\( \ V=V_{0} \ \)であるとき,発電機の内部電圧\( \ E \ \)を\( \ V_{0} \ \),\( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {e}} \ \)を用いて表せ。ここで,\( \ {\dot I}_{1}={\dot I}_{2} \ \)であり,かつ複素数\( \ a + \mathrm {j}b=c \left( a,b,c \right. \ \)は実数\( \left. \right) \ \)について\( \ a^{2} + b^{2}=c^{2} \ \)が成立することを用いよ。
(5) \( \ V=V_{0} \ \)かつ\( \ \displaystyle X_{\mathrm {e}}=\frac {1}{2}X_{\mathrm {d}} \ \)のとき,安定に送電できる有効電力の最大値を\( \ V_{0} \ \)と\( \ X_{\mathrm {d}} \ \)を用いて表せ。ただし,小じょう乱同期安定性以外の制約条件は無視せよ。
【ワンポイント解説】
発電所から無限大母線に接続する際の送電電力を検討する問題です。
考え方自体は難解ではなく(1)~(3)までは標準的な問題ですが,(4)の計算に時間を要する問題です。
\( \ 1 \ \)種受験生ですと(4)もある程度解ける受験生もいるかもしれませんが,合格を目指す上では(1)~(3)を確実に正答しておくことが重要となるかと思います。
1.複素平面における複素数の表記方法
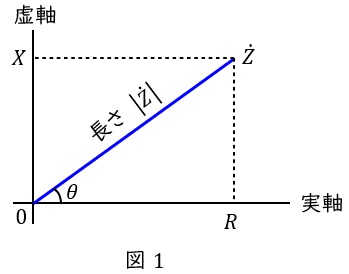
図1のような複素空間上の値\( \ \dot Z =R+\mathrm {j}X \ \)において,以下のような表記方法が定義されます。
ただし,\( \ \dot Z \ \)の絶対値\( \ \left| \dot Z\right| = \sqrt {R^{2}+X^{2}} \ \),\( \ \dot Z \ \)と実軸となす角を\( \ \theta \ \)とします。
①直交座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \left( \cos \theta +\mathrm {j}\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
②指数表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| \mathrm {e}^{\mathrm {j}\theta } \\[ 5pt ]
\end{eqnarray}
\]
ただし,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これをオイラーの公式といいます。
③極座標表記
\[
\begin{eqnarray}
\dot Z &=&\left| \dot Z\right| ∠\theta \\[ 5pt ]
\end{eqnarray}
\]
2.複素電力
三相線路において,送電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端電圧(相電圧)を\( \ {\dot E}_{\mathrm {r}} \ \mathrm {[V]} \ \),線路電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3{\dot E}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
3.無限大母線に接続するときの有効電力\( \ P \ \)と無効電力\( \ Q \ \)
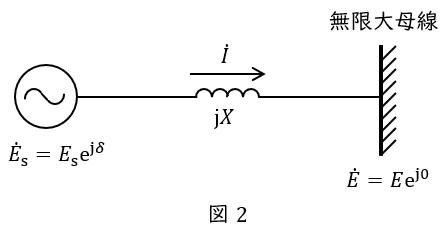
図2のような無限大母線(相電圧\( \ \dot E=E\mathrm {e}^{\mathrm {j}0}=E \ \))にリアクタンス\( \ X \ \)を介して接続する発電機(相電圧\( \ {\dot E}_{\mathrm {s}}=E_{\mathrm {s}}\mathrm {e}^{\mathrm {j}\delta } \ \))の三相の複素電力\( \ P+\mathrm {j}Q \ \)を考えます。ただし,線路等の抵抗分は十分小さく無視するものとします。
リアクタンスを流れる電流を\( \ \dot I \ \)とすると,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}-\dot E&=&\mathrm {j}X\dot I \\[ 5pt ]
\dot I&=&\frac {{\dot E}_{\mathrm {s}} -\dot E}{\mathrm {j}X} \\[ 5pt ]
\dot I&=&\frac {E_{\mathrm {s}}\mathrm {e}^{\mathrm {j}\delta } -E}{\mathrm {j}X} \\[ 5pt ]
\end{eqnarray}
\]
となり,複素電力\( \ P+\mathrm {j}Q \ \)は,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3\dot E\overline {\dot I} \\[ 5pt ]
&=&3E\cdot \frac {E_{\mathrm {s}}\mathrm {e}^{-\mathrm {j}\delta } -E}{-\mathrm {j}X} \\[ 5pt ]
&=&\mathrm {j}3E\cdot \frac {E_{\mathrm {s}}\left( \cos \delta -\mathrm {j}\sin \delta \right) -E}{X} \\[ 5pt ]
&=&\frac {\mathrm {j}3E_{\mathrm {s}}E\left( \cos \delta -\mathrm {j}\sin \delta \right) -\mathrm {j}3E^{2}}{X} \\[ 5pt ]
&=&\frac {\mathrm {j}3E_{\mathrm {s}}E\cos \delta +3E_{\mathrm {s}}E\sin \delta -\mathrm {j}3E^{2}}{X} \\[ 5pt ]
&=&\frac {3E_{\mathrm {s}}E\sin \delta + \mathrm {j}3\left( E_{\mathrm {s}}E\cos \delta -E^{2}\right) }{X} \\[ 5pt ]
&=&\frac {3E_{\mathrm {s}}E\sin \delta }{X}+\mathrm {j}\frac {3\left( E_{\mathrm {s}}E\cos \delta -E^{2}\right) }{X} \\[ 5pt ]
\end{eqnarray}
\]
となります。両辺比較すると,
\[
\begin{eqnarray}
P&=&\frac {3E_{\mathrm {s}}E\sin \delta }{X} \\[ 5pt ]
Q&=&\frac {3\left( E_{\mathrm {s}}E\cos \delta -E^{2}\right) }{X} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。ここで,線間電圧の大きさ\( \ V_{\mathrm {s}}=\sqrt {3}E_{\mathrm {s}} \ \),\( \ V=\sqrt {3}E \ \)とすれば,
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V\sin \delta }{X} \\[ 5pt ]
Q&=&\frac { V_{\mathrm {s}}V\cos \delta -V^{2} }{X} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)無限大母線の受電電力\( \ P \ \)及び\( \ Q \ \)を,\( \ E \ \),\( \ V_{0} \ \),\( \ \alpha \ \),\( \ \beta \ \),\( \ X_{\mathrm {d}} \ \),\( \ X_{\mathrm {e}} \ \)を用いて表す
ワンポイント解説「3.無限大母線に接続するときの有効電力\( \ P \ \)と無効電力\( \ Q \ \)」の通り,本問においては\( \ V_{\mathrm {s}}→E \ \),\( \ V→V_{\mathrm {0}} \ \),\( \ \delta →\alpha +\beta \ \),\( \ X→X_{\mathrm {d}}+X_{\mathrm {e}} \ \)として,同様に求めると,
\[
\begin{eqnarray}
P&=&\frac {EV_{\mathrm {0}}\sin \left( \alpha +\beta \right) }{X_{\mathrm {d}}+X_{\mathrm {e}}} \\[ 5pt ]
Q&=&\frac { EV_{\mathrm {0}}\cos \left( \alpha +\beta \right) -V_{\mathrm {0}}^{2} }{X_{\mathrm {d}}+X_{\mathrm {e}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)同期化力により定まる小じょう乱同期安定性の観点から,安定な送電のために\( \ \alpha + \beta \ \)が満たすべき条件
(1)解答式において,\( \ \alpha +\beta =\delta \ \)とおくと,
\[
\begin{eqnarray}
P&=&\frac {EV_{\mathrm {0}}}{X_{\mathrm {d}}+X_{\mathrm {e}}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,同期化力\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta } \ \)は,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta }&=&\frac {EV_{\mathrm {0}}}{X_{\mathrm {d}}+X_{\mathrm {e}}}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta }≧0 \ \)のとき安定な送電が可能なので,
\[
\begin{eqnarray}
\frac {EV_{\mathrm {0}}}{X_{\mathrm {d}}+X_{\mathrm {e}}}\cos \delta &≧&0 \\[ 5pt ]
\cos \delta &≧&0 \\[ 5pt ]
0<\delta &≦&\frac {\pi}{2} \\[ 5pt ]
0<\alpha +\beta &≦&\frac {\pi}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(\( \ 0 \ \)を含まないのは題意より\( \ \alpha > 0 \ \),\( \ \beta > 0 \ \)のためです。)
(3)図の\( \ \mathrm {j}X_{\mathrm {d}} \ \)を流れる電流\( \ {\dot I}_{1} \ \),\( \ \mathrm {j}X_{\mathrm {e}} \ \)を流れる電流\( \ {\dot I}_{2} \ \)
ワンポイント解説「3.無限大母線に接続するときの有効電力\( \ P \ \)と無効電力\( \ Q \ \)」と同様に考えれば,
\[
\begin{eqnarray}
E\mathrm {e}^{\mathrm {j}\alpha }-V\mathrm {e}^{\mathrm {j}0 }&=&\mathrm {j}X_{\mathrm {d}}{\dot I}_{1} \\[ 5pt ]
{\dot I}_{1}&=&\frac {E\mathrm {e}^{\mathrm {j}\alpha }-V}{\mathrm {j}X_{\mathrm {d}}} \\[ 5pt ]
V\mathrm {e}^{\mathrm {j}0 }-V_{0}\mathrm {e}^{-\mathrm {j}\beta }&=&\mathrm {j}X_{\mathrm {e}}{\dot I}_{2} \\[ 5pt ]
{\dot I}_{2}&=&\frac {V-V_{0}\mathrm {e}^{-\mathrm {j}\beta }}{\mathrm {j}X_{\mathrm {e}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)小じょう乱同期安定限界において\( \ V=V_{0} \ \)であるときの発電機の内部電圧\( \ E \ \)
(3)解答式において,題意より\( \ V=V_{0} \ \)かつ\( \ {\dot I}_{1}={\dot I}_{2} \ \)であるから,
\[
\begin{eqnarray}
\frac {E\mathrm {e}^{\mathrm {j}\alpha }-V_{0}}{\mathrm {j}X_{\mathrm {d}}}&=&\frac {V_{0}-V_{0}\mathrm {e}^{-\mathrm {j}\beta }}{\mathrm {j}X_{\mathrm {e}}} \\[ 5pt ]
\frac {E\mathrm {e}^{\mathrm {j}\alpha }-V_{0}}{X_{\mathrm {d}}}&=&\frac {V_{0}-V_{0}\mathrm {e}^{-\mathrm {j}\beta }}{X_{\mathrm {e}}} \\[ 5pt ]
\end{eqnarray}
\]
が成立する。これを整理していくと,
\[
\begin{eqnarray}
\frac {E\left( \cos \alpha +\mathrm {j}\sin \alpha \right) -V_{0}}{X_{\mathrm {d}}}&=&\frac {V_{0}-V_{0} \left( \cos \beta -\mathrm {j}\sin \beta \right) }{X_{\mathrm {e}}} \\[ 5pt ]
EX_{\mathrm {e}}\left( \cos \alpha +\mathrm {j}\sin \alpha \right) -V_{0}X_{\mathrm {e}}&=&V_{0}X_{\mathrm {d}}-V_{0}X_{\mathrm {d}}\left( \cos \beta -\mathrm {j}\sin \beta \right) \\[ 5pt ]
EX_{\mathrm {e}}\left( \cos \alpha +\mathrm {j}\sin \alpha \right) +V_{0}X_{\mathrm {d}}\left( \cos \beta -\mathrm {j}\sin \beta \right) &=&V_{0}X_{\mathrm {d}}+V_{0}X_{\mathrm {e}} \\[ 5pt ]
EX_{\mathrm {e}}\cos \alpha +V_{0}X_{\mathrm {d}}\cos \beta +\mathrm {j}\left( EX_{\mathrm {e}}\sin \alpha – V_{0}X_{\mathrm {d}}\sin \beta \right) &=&V_{0}\left( X_{\mathrm {d}}+X_{\mathrm {e}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,(2)解答式より,小じょう乱同期安定限界において\( \ \displaystyle \alpha + \beta =\frac {\pi}{2} \ \)であるから,
\[
\begin{eqnarray}
\cos \beta &=&\cos \left( \frac {\pi}{2}-\alpha \right) \\[ 5pt ]
&=&\cos \frac {\pi}{2}\cos \alpha +\sin \frac {\pi}{2}\sin \alpha \\[ 5pt ]
&=&\sin \alpha \\[ 5pt ]
\sin \beta &=&\sin \left( \frac {\pi}{2}-\alpha \right) \\[ 5pt ]
&=&\sin \frac {\pi}{2}\cos \alpha -\cos \frac {\pi}{2}\sin \alpha \\[ 5pt ]
&=&\cos \alpha \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,
\[
\begin{eqnarray}
EX_{\mathrm {e}}\cos \alpha +V_{0}X_{\mathrm {d}}\sin \alpha +\mathrm {j}\left( EX_{\mathrm {e}}\sin \alpha – V_{0}X_{\mathrm {d}}\cos \alpha \right) &=&V_{0}\left( X_{\mathrm {d}}+X_{\mathrm {e}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに問題文の通り,「複素数\( \ a + \mathrm {j}b=c \left( a,b,c \right. \ \)は実数\( \left. \right) \ \)について\( \ a^{2} + b^{2}=c^{2} \ \)が成立する」となっていることから,
\[
\begin{eqnarray}
\left( EX_{\mathrm {e}}\cos \alpha +V_{0}X_{\mathrm {d}}\sin \alpha \right) ^{2}+\left( EX_{\mathrm {e}}\sin \alpha – V_{0}X_{\mathrm {d}}\cos \alpha \right) ^{2} &=& V_{0}^{2}\left( X_{\mathrm {d}}+X_{\mathrm {e}}\right) ^{2} \\[ 5pt ]
E^{2}X_{\mathrm {e}}^{2}\cos ^{2}\alpha +2EV_{0}X_{\mathrm {d}}X_{\mathrm {e}}\sin \alpha \cos \alpha +V_{0}^{2}X_{\mathrm {d}}^{2}\sin ^{2}\alpha +E^{2}X_{\mathrm {e}}^{2}\sin ^{2}\alpha -2EV_{0}X_{\mathrm {d}}X_{\mathrm {e}}\sin \alpha \cos \alpha +V_{0}^{2}X_{\mathrm {d}}^{2}\cos ^{2}\alpha &=& V_{0}^{2}\left( X_{\mathrm {d}}+X_{\mathrm {e}}\right) ^{2} \\[ 5pt ]
E^{2}X_{\mathrm {e}}^{2}\left( \cos ^{2}\alpha +\sin ^{2}\alpha \right) +V_{0}^{2}X_{\mathrm {d}}^{2}\left( \sin ^{2}\alpha +\cos ^{2}\alpha \right) &=& V_{0}^{2}\left( X_{\mathrm {d}}+X_{\mathrm {e}}\right) ^{2} \\[ 5pt ]
E^{2}X_{\mathrm {e}}^{2}+V_{0}^{2}X_{\mathrm {d}}^{2}&=& V_{0}^{2}\left( X_{\mathrm {d}}+X_{\mathrm {e}}\right) ^{2} \\[ 5pt ]
E^{2}X_{\mathrm {e}}^{2}&=& V_{0}^{2}X_{\mathrm {d}}^{2}+2V_{0}^{2}X_{\mathrm {d}}X_{\mathrm {e}}+V_{0}^{2}X_{\mathrm {e}}^{2}-V_{0}^{2}X_{\mathrm {d}}^{2} \\[ 5pt ]
&=&2V_{0}^{2}X_{\mathrm {d}}X_{\mathrm {e}}+V_{0}^{2}X_{\mathrm {e}}^{2} \\[ 5pt ]
E^{2}&=&2V_{0}^{2}\frac {X_{\mathrm {d}}}{X_{\mathrm {e}}}+V_{0}^{2} \\[ 5pt ]
&=&V_{0}^{2}\left( \frac {2X_{\mathrm {d}}}{X_{\mathrm {e}}}+1\right) \\[ 5pt ]
E&=&V_{0}\sqrt { \frac {2X_{\mathrm {d}}}{X_{\mathrm {e}}}+1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ V=V_{0} \ \)かつ\( \ \displaystyle X_{\mathrm {e}}=\frac {1}{2}X_{\mathrm {d}} \ \)のとき,安定に送電できる有効電力の最大値
(1)解答式において,安定に送電できる有効電力の最大値\( \ P_{\mathrm {m}} \ \)は\( \ 0<\sin \left( \alpha +\beta \right) ≦1 \ \)より,
\[
\begin{eqnarray}
P_{\mathrm {m}} &=&\frac {EV_{\mathrm {0}}}{X_{\mathrm {d}}+X_{\mathrm {e}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。これに,(4)解答式及び\( \ \displaystyle X_{\mathrm {e}}=\frac {1}{2}X_{\mathrm {d}} \ \)を代入すると,
\[
\begin{eqnarray}
P_{\mathrm {m}} &=&\frac {\displaystyle V_{0}\sqrt { \frac {2X_{\mathrm {d}}}{X_{\mathrm {e}}}+1}\cdot V_{\mathrm {0}}}{\displaystyle X_{\mathrm {d}}+\frac {1}{2}X_{\mathrm {d}}} \\[ 5pt ]
&=&\frac {\displaystyle V_{0}^{2}\sqrt { \frac {2X_{\mathrm {d}}}{\displaystyle \frac {1}{2}X_{\mathrm {d}}}+1}}{\displaystyle \frac {3}{2}X_{\mathrm {d}}} \\[ 5pt ]
&=&\frac {\displaystyle V_{0}^{2}\sqrt { 4+1}}{\displaystyle \frac {3}{2}X_{\mathrm {d}}} \\[ 5pt ]
&=&\frac {2\sqrt {5}V_{0}^{2}}{3X_{\mathrm {d}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん