《機械》〈変圧器〉[H20:問3]主回路に過電流が発生した時の変流器の特性に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，「変流器（保護リレー用）」（以下「変流器」と略す。）の特性に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句を解答群の中から選び，その記号をマークシートに記入しなさい。

保護リレーと組み合わせて使用される変流器では，系統短絡事故時の過電流で変流比誤差が変化すると，保護リレーの誤・不動作の原因となるため，過電流域でも一次電流と二次電流の比例関係が良好に維持されることが必要である。

変流器の過電流域での特性の一つとして過電流定数がある。過電流定数は，電気学会　電気規格調査会標準規格$ \ \mathrm {JEC-1201-1996} \ $の中で，「定格二次負担（力率$ \ 0.8 \ $遅れ電流）のもとで，定格周波数の電流を流して比誤差を試験したとき，その値が$ \ \fbox {　（１）　} \ $になるときの一次電流を定格一次電流で除した値」と決められている。変流器の銘板に記載される過電流定数は，定格二次負担における数値で示される。

短絡電流が大きな回路に，定格一次電流の小さな変流器を用いる場合には，過電流定数の大きな変流器が必要で，定格一次電流での$ \ \fbox {　（２）　} \ $を小さくする必要がある。しかしながら，変流器の$ \ \fbox {　（３）　} \ $抵抗値が小さければ（過電流定数$ \ \times \fbox {　（４）　} \ $）の値はほぼ一定となるので，二次回路に接続される電線路や器具類のインピーダンスによって，実用的な過電流定数は変化する。

一般に，主回路の短絡事故電流には減衰する直流分が含まれる。この直流分電流によって変流器鉄心が偏磁や飽和を起こし，事故発生から数サイクルの間正確な変流器二次電流が得られない場合がある。このような短絡事故電流に対して，高速度で確実な保護リレーの動作を得るための変流器として，磁路にギャップを設ける等の対策を施した$ \ \fbox {　（５）　} \ $付変流器を使用することもある。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　定格二次負担　　　　　&（ロ）&　磁束密度　　　　　&（ハ）&　過渡特性 \\[ 5pt ] &（ニ）&　起電力　　　　　&（ホ）&　一次巻線　　　　　&（ヘ）&　-5.0 \ \mathrm {[％]} \\[ 5pt ] &（ト）&　定格二次電流　　　　　&（チ）&　定格負荷　　　　　&（リ）&　起磁力 \\[ 5pt ] &（ヌ）&　-10 \ \mathrm {[％]}　　　　　&（ル）&　励磁特性　　　　　&（ヲ）&　二次巻線 \\[ 5pt ] &（ワ）&　可飽和特性　　　　　&（カ）&　磁　気　　　　　&（ヨ）&　過電流定数値 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

変流器の過電流定数に関する問題です。
過電流定数に関しては現場のリレーを扱う方で見たことがある人も多いと思いますが，定義等をしっかりと理解されている方は少なかったと予想されます。
また，専門書からの引用かもしれませんが，問題分の言い回しが理解しにくいため，その辺りも受験生を悩ませた問題かと思います。

1.変流器の等価回路（二次換算）
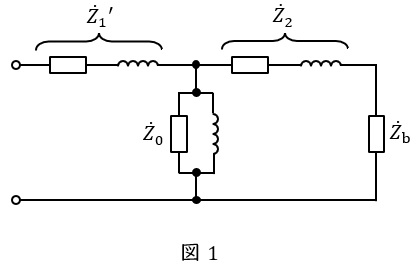
変流器の二次換算等価回路は図1のようになり，変圧器の等価回路とほぼ同じ形をしています。$ \ {\dot Z}_{0} \ \mathrm {[\Omega ]} \ $が励磁インピーダンス，$ \ {{\dot Z}_{1}}^{\prime } \ \mathrm {[\Omega ]} \ $が二次側に換算した一次側インピーダンス，$ \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ $が二次側インピーダンス，$ \ {\dot Z}_{\mathrm {b}} \ \mathrm {[\Omega ]} \ $が計器や保護リレー等の二次負担となります。
等価回路からもわかるように，励磁回路の分だけ測定値の誤差を生じることになります。

2.過電流定数
$ \ \mathrm {JEC} \ $において，「定格二次負担（力率$ \ 0.8 \ $遅れ電流）のもとで，定格周波数の電流を流して比誤差を試験したとき，その値が$ \ -10 \ \mathrm {％} \ $になるときの一次電流を定格一次電流で除した値」と定義される定数です。
理想的な変流器では，一次電流に比例して二次電流は増加していきますが，ある一定以上の過電流が流れると，鉄心の磁気飽和等により，二次電流が比例せずに小さくなっていき誤差が大きくなっていきます。この理想変流器との誤差が$ \ 10 \ \mathrm {％} \ $となるときの一次電流の定格一次電流に対する割合を過電流定数といいます。

【解答】

(1)解答：ヌ
題意より解答候補は，（ヘ）$ \ -5.0 \ \mathrm {[％]} \ $，（ヌ）$ \ -10 \ \mathrm {[％]} \ $，（ヨ）過電流定数値$ \ \mathrm {[％]} \ $，になると思います。
ワンポイント解説「2.過電流定数」の通り，過電流定数は定格二次負担（力率$ \ 0.8 \ $遅れ電流）のもとで，定格周波数の電流を流して比誤差を試験したとき，その値が$ \ -10 \ \mathrm {[％]} \ $になるときの一次電流を定格一次電流で除した値となります。

(2)解答：ロ
題意より解答候補は，（ロ）磁束密度，（ニ）起電力，（リ）起磁力，等になると思います。
ワンポイント解説「1.変流器の等価回路（二次換算）」及び「2.過電流定数」の通り，短絡電流が大きな回路に，定格一次電流の小さな変流器を用いる場合には，過電流定数の大きな変流器が必要となります。言い換えると，定格一次電流での磁束密度を小さくする必要があります。

(3)解答：ヲ
題意より解答候補は，（ホ）一次巻線，（ヲ）二次巻線，になると思います。
ワンポイント解説「1.変流器の等価回路（二次換算）」の通り，変流器の二次巻線抵抗値が小さければ，二次回路に接続される電線路や器具類のインピーダンスによって，実用的な過電流定数は変化することになります。

(4)解答：イ
題意より解答候補は，（イ）定格二次負担，（ト）定格二次電流，（チ）定格負荷，になると思います。
問題文に示されているように，過電流定数は定格二次負担における数値で示され，二次巻線抵抗値が小さければ過電流定数$ \ \times \ $定格二次負担はほぼ一定の値となります。

(5)解答：ハ
題意より解答候補は，（ハ）過渡特性，（ル）励磁特性，（ワ）可飽和特性，になると思います。
主回路の短絡事故電流には減衰する直流分が含まれることがあり，高速度で確実な保護リレーの動作を得るための変流器として，鉄心にギャップを設ける等の対策を施した変流器を過渡特性付変流器といいます。