《機械》〈回転機〉[H22:問1]かご形誘導電動機の始動時異常現象に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，かご形誘導電動機の始動時異常現象に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句を解答群の中から選びなさい。

誘導機のギャップの磁束密度分布は，基本波のほかに多くの高調波成分が含まれる。これらの高調波成分の作用によって下記のような始動時の電磁異常現象を発生することがある。

かご形回転子に固定子高調波回転磁界に起因する電流が流れ，その作用で誘導機性のトルクを生じる。このトルクを高調波$ \ \fbox {　（１）　} \ $という。このようなトルクが存在すると，これらが基本波によって発生するトルクと合成され，滑りの大きい付近でトルクの谷を生じることがあり，そのトルクの谷が負荷の要求するトルクよりも$ \ \fbox {　（２）　} \ $なると，始動時にはこの付近の速度までしか加速できなくなる。このような現象を$ \ \fbox {　（３）　} \ $といい，この状態が持続すると，電動機には始動電流に近い大きな電流が流れ続けるので焼損に至る。

ある高調波の固定子回転磁界と同じ速度をもつ回転子高調波回転磁界が存在すると，その回転速度に相当する滑りにおいて同期機性のトルクが発生する。これを高調波$ \ \fbox {　（４）　} \ $という。回転子高調波磁界の速度が固定子高調波磁界の速度から少しでも外れると，このトルクは失われる。このトルクが大きい場合はその滑りにおいて前述と同じような現象を生じる。

いずれの場合でも$ \ \fbox {　（５）　} \ $の採用はこの現象に対する有効な軽減策の一つである。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　脱出トルク　　　　　&（ロ）&　磁極ピッチ　　　　　&（ハ）&　斜めスロット \\[ 5pt ] &（ニ）&　ステッピング　　　　　　&（ホ）&　引入トルク　　　　　&（ヘ）&　高　く \\[ 5pt ] &（ト）&　クローリング　　　　　&（チ）&　小さく　　　　　&（リ）&　大きく \\[ 5pt ] &（ヌ）&　制動トルク　　　　　&（ル）&　サンプリング　　　　　　&（ヲ）&　巻線ピッチ \\[ 5pt ] &（ワ）&　始動トルク　　　　　&（カ）&　同期トルク　　　　　&（ヨ）&　非同期トルク \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

かご形誘導電動機の始動時異常現象に関する問題です。
クローリング現象は専門書を見ると数式等が掲載されていますが，電験対策としては概要を覚えておくだけで十分かと思います。

1.クローリング現象
かご形誘導電動機を全電圧始動する際に速度の低い領域で，それ以上加速しないで電流が大きい状態でとどまることをいいます。

三相巻線は，各巻線が対称的に配置されているため偶数次の高調波は発生せず，奇数次の高調波が発生します。そのうち，第$ \ 3 \ $，第$ \ 9 \ $，第$ \ 15 \ $調波等の第$ \ 3n \ $調波に関しては，各巻線の軸と同相となり，ギャップ中に回転磁界は生じません。

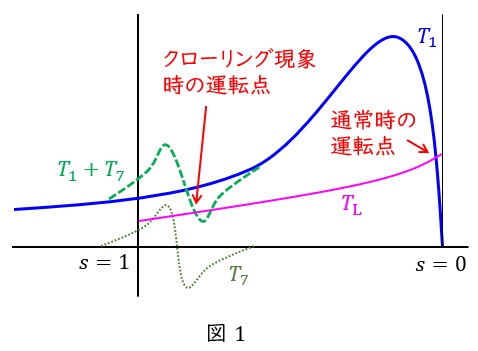
ワンポイント解説「2.空間高調波が含まれる際の回転磁界」の通り，第$ \ 5 \ $，第$ \ 11 \ $調波等の$ \ 6n-1 \ $成分の高調波は回転子とは逆向きに，第$ \ 7 \ $，第$ \ 13 \ $調波等の$ \ 6n+1 \ $成分の高調波は回転子と同じ向きに回転し，回転子に電流を誘導して，例えば第$ \ 7 \ $調波であれば図1に示すようなトルク$ \ T_{\mathrm {7}} \ $を発生します。

この$ \ T_{\mathrm {7}} \ $と基本波のトルク$ \ T_{\mathrm {1}} \ $が重畳されると，図1の$ \ T_{\mathrm {1}}+T_{\mathrm {7}} \ $に示すようなトルク曲線となり，これが負荷トルク$ \ T_{\mathrm {L}} \ $よりも小さくなると，この付近の速度までしか加速できなくなり，電動機には大きな電流が流れるので焼損する可能性があります。

2.空間高調波が含まれる際の回転磁界（参考）
$ \ \mathrm {a} \ $相を基準として，各相から発生された起磁力を，
\[
\begin{eqnarray}
F_{\mathrm {a}}&=&F\cos \omega t \\[ 5pt ] F_{\mathrm {b}}&=&F\cos \left( \omega t-\frac {2}{3}\pi \right) \\[ 5pt ] F_{\mathrm {c}}&=&F\cos \left( \omega t-\frac {4}{3}\pi \right) \\[ 5pt ] \end{eqnarray}
\] と置きます。第$ \ k \ $空間高調波による影響を考慮すると，
\[
\begin{eqnarray}
F_{\mathrm {ak}}&=&F\cos \omega t \sin k \theta \\[ 5pt ] F_{\mathrm {bk}}&=&F\cos \left( \omega t-\frac {2}{3}\pi \right) \sin k \left( \theta-\frac {2}{3}\pi \right) \\[ 5pt ] F_{\mathrm {ck}}&=&F\cos \left( \omega t-\frac {4}{3}\pi \right) \sin k \left( \theta-\frac {4}{3}\pi \right) \\[ 5pt ] \end{eqnarray}
\] となり，加法定理$ \ \sin \left( \alpha ±\beta \right) =\sin \alpha \cos \beta ±\cos \alpha \sin \beta \ $の関係より，
\[
\begin{eqnarray}
\cos \alpha \sin \beta &=&\frac {1}{2}\left[ \sin \left( \alpha +\beta \right) -\sin \left( \alpha -\beta \right) \right] \\[ 5pt ] \end{eqnarray}
\] が成り立つから，
\[
\begin{eqnarray}
F_{\mathrm {ak}}&=&\frac {F}{2}\left[ \sin \left( \omega t +k \theta \right) -\sin \left( \omega t -k \theta \right) \right] \\[ 5pt ] F_{\mathrm {bk}}&=&\frac {F}{2}\left[ \sin \left\{ \omega t-\frac {2}{3}\pi +k \left( \theta-\frac {2}{3}\pi \right) \right\} -\sin \left\{ \omega t-\frac {2}{3}\pi -k \left( \theta-\frac {2}{3}\pi \right) \right\} \right] \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {2}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {2}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] F_{\mathrm {ck}}&=&\frac {F}{2}\left[ \sin \left\{ \omega t-\frac {4}{3}\pi +k \left( \theta-\frac {4}{3}\pi \right) \right\} -\sin \left\{ \omega t-\frac {4}{3}\pi -k \left( \theta-\frac {4}{3}\pi \right) \right\} \right] \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {4}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {4}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] \end{eqnarray}
\] となります。それぞれの起磁力を足し合わせると，
\[
\begin{eqnarray}
F_{\mathrm {k}}&=&F_{\mathrm {ak}}+F_{\mathrm {bk}}+F_{\mathrm {ck}} \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left( \omega t +k \theta \right) -\sin \left( \omega t -k \theta \right) \right]+\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {2}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {2}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] &&+\frac {F}{2}\left[ \sin \left\{ \omega t+k\theta -\frac {4}{3}\left( 1+k \right) \pi \right\} -\sin \left\{ \omega t-k\theta -\frac {4}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] &=&\frac {F}{2}\left[ \sin \left( \omega t +k \theta \right)+\sin \left\{ \omega t+k\theta -\frac {2}{3}\left( 1+k \right) \pi \right\} +\sin \left\{ \omega t+k\theta -\frac {4}{3}\left( 1+k \right) \pi \right\} \right] \\[ 5pt ] &&-\frac {F}{2}\left[ \sin \left( \omega t -k \theta \right)+\sin \left\{ \omega t-k\theta -\frac {2}{3}\left( 1-k \right) \pi \right\} +\sin \left\{ \omega t-k\theta -\frac {4}{3}\left( 1-k \right) \pi \right\} \right] \\[ 5pt ] \end{eqnarray}
\] と整理できます。上式は第一項が逆方向成分，第二項が順方向成分になることがわかります。$ \ k=7，13，・・・ \ $を代入すると，第一項の逆方向成分が零となり順方向の回転磁界が発生し，$ \ k=5，11，・・・ \ $を代入すると，第二項の順方向成分が零となり逆方向の回転磁界が発生し，$ \ k=3，9，・・・ \ $を代入すると，第一項，第二項とも零となり，回転磁界が発生しないことが分かります。

【解答】

(1)解答：ヨ
題意より解答候補は，（イ）脱出トルク，（ホ）引入トルク，（ヌ）制動トルク，（ワ）始動トルク，（カ）同期トルク，（ヨ）非同期トルク，になると思います。
かご形回転子に固定子高調波回転磁界に起因する電流が流れ，これにより生じる誘導機性のトルクは，主に滑り$ \ s=1 \ $付近に現れるトルクで高調波非同期トルクといいます。

(2)解答：チ
題意より解答候補は，（ヘ）高く，（チ）小さく，（リ）大きく，になると思います。
ワンポイント解説「1.クローリング現象」の通り，基本波と高調波のトルクが重畳することでトルクの谷を生じることがあり，そのトルクの谷が負荷の要求するトルクよりも小さくなると，この付近の速度までしか加速できなくなります。

(3)解答：ト
題意より解答候補は，（ニ）ステッピング，（ト）クローリング，（ル）サンプリング，になると思います。
ワンポイント解説「1.クローリング現象」の通り，問題文の現象をクローリング現象といいます。

(4)解答：カ
題意より解答候補は，（イ）脱出トルク，（ホ）引入トルク，（ヌ）制動トルク，（ワ）始動トルク，（カ）同期トルク，（ヨ）非同期トルク，になると思います。
ある高調波の固定子回転磁界と同じ速度をもつ回転子高調波回転磁界が存在すると，その回転速度に相当する滑りにおいて同期機性のトルクが発生し，これを高調波同期トルクといいます。

(5)解答：ハ
題意より解答候補は，（ロ）磁極ピッチ，（ハ）斜めスロット，（ヲ）巻線ピッチ，になると思います。
このうち，斜めスロットの採用はクローリング現象の軽減に有効とされています。