《機械》〈同期機〉[H20:問5]交流回転機の分布係数に関する計算・空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，交流回転機の分布係数に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句又は式を解答群の中から選び，その記号を記述用紙の解答欄に記入しなさい。

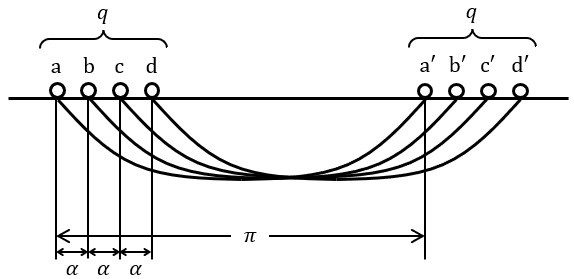
交流回転機の固定子又は回転子に電気角\( \ \displaystyle \frac {2\pi }{3} \ \mathrm {[rad]} \ \)の間隔で\( \ 3 \ \)個の等しい巻線を配置する。ただし，巻数はすべて\( \ W \ \)とし，\( \ 1 \ \)個の巻線は一つのスロットに収められた集中巻とする。これらに角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)，実効値\( \ I \ \mathrm {[A]} \ \)の対称三相交流電流を流した場合，\( \ 1 \ \)個の巻線によって生じる回転方向に沿った起磁力の空間分布は\( \ \fbox {　 （１） 　} \ \)波となり，その最大値は\( \ W \left( \sqrt {2}I \right) \ \mathrm {[A]} \ \)である。\( \ 3 \ \)個の巻線によって生じる合成起磁力の基本波成分は，電気角で表した進行速度が\( \ \omega \ \mathrm {[rad / s]} \ \)，最大値が\( \ \displaystyle \frac {4}{\pi }W\left( \sqrt {2}I \right) \frac {3}{2} \ \mathrm {[A]} \ \)の正弦波進行波となる。そのほかに\( \ \fbox {　 （２） 　} \ \)次の空間高調波起磁力も生じ，回転機の特性を害する原因ともなる。これらの空間高調波を低減する巻線法として，分布巻がある。これは巻線が図のように\( \ q \ \)個のスロットに分布され，これらが直列に接続されているような巻線法である。スロットピッチを\( \ \alpha \ \mathrm {[rad]} \ \)とし，\( \ \mathrm {aa^{\prime }} \ \)，\( \ \mathrm {bb^{\prime }} \ \)，\( \ \mathrm {cc^{\prime }} \ \)，\( \ \cdots \ \)に収められた各コイルの電流によって生じる基本波起磁力は大きさが等しく，空間で順次\( \ \alpha \ \)の位相差を持った正弦波であるから，これらをベクトルで表すと，\( \ {\dot f}_{1}=f \ \)，\( \ {\dot f}_{2}=fe^{-j\alpha } \ \)，\( \ {\dot f}_{3}=fe^{-j2\alpha } \ \)，\( \ \cdots \ \)，\( \ {\dot f}_{q}=fe^{-j\left( q-1\right) \alpha } \ \)となる。ただし，基本波起磁力の大きさを\( \ f \ \)とする。これらのベクトル和である合成起磁力ベクトル\( \ \dot F \ \)は，公比を\( \ e^{-j\alpha } \ \)とする等比級数であるから，\( \ \dot F= \ \fbox {　 （３） 　} \ \)となる。その大きさを\( \ F \ \)とすると，集中巻の基本波起磁力の大きさは\( \ qf \ \)であるから，集中巻に比べて\( \ \displaystyle \frac {F}{qf} \ \)に減少する。この比を分布係数\( \ k_{d1} \ \)といい，\( \ 1 \ \)より小さく，\( \ k_{d1}= \ \fbox {　 （４） 　} \ \)となる。第\( \ n \ \)次空間高調波に対する分布係数\( \ k_{dn} \ \)は\( \ k_{dn}= \ \fbox {　 （５） 　} \ \)となり，個数\( \ q \ \)が増加すると，高調波成分は急激に減少し，また，高調波次数が高いほど減少が顕著となり，集中巻に比べ分布巻の合成起磁力は正弦波に近づく。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　実　数　　　　　&（ロ）&　三　角　　　　　&（ハ）&　方　形 \\[ 5pt ] &（ニ）&　偶　数　　　　　&（ホ）&　のこぎり　　　　　&（ヘ）&　奇　数 \\[ 5pt ] &（ト）&　f\frac {1-e^{-jq\alpha }}{1+e^{-j\alpha }}　　　　　&（チ）&　\frac {\displaystyle \cos \left( \frac {q\alpha }{2}\right) }{\displaystyle q\sin \left( \frac {\alpha }{2}\right) }　　　　　&（リ）&　\frac {\displaystyle \sin \left( \frac {qn\alpha }{2}\right) }{\displaystyle q\sin \left( \frac {n\alpha }{2}\right) } \\[ 5pt ] &（ヌ）&　\frac {\displaystyle \sin \left( \frac {qn\alpha }{2}\right) }{ q\sin \left( n\alpha \right) }　　　　　&（ル）&　\frac {\displaystyle \sin \left( \frac {q\alpha }{2}\right) }{\displaystyle q\sin \left( \frac {\alpha }{2}\right) }　　　　　&（ヲ）&　f\frac {1+e^{-jq\alpha }}{1-e^{-j\alpha }} \\[ 5pt ] &（ワ）&　\frac {\displaystyle \cos \left( \frac {qn\alpha }{2}\right) }{\displaystyle q\sin \left( \frac {n\alpha }{2}\right) }　　　　　&（カ）&　f\frac {1-e^{-jq\alpha }}{1-e^{-j\alpha }}　　　　　&（ヨ）&　\frac {\displaystyle \sin \left( \frac {q\alpha }{2}\right) }{ q\sin \left( \alpha \right) } \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流回転機に採用される分布巻に関する問題です。
前半の(1)や(2)は\( \ 2 \ \)種や\( \ 3 \ \)種でも出題されたことがある問題なのでできれば正答しておきたい空欄，後半の(3)からは数学力が問われている空欄です。数学が苦手な方の\( \ 1 \ \)種攻略はかなり厳しいので，しっかりと数学の基礎を固めて試験に挑むようにして下さい。

1.同期発電機のコイルの巻き方の違い
同期発電機の電機子巻線の巻き方や接続方法は大きく分けて集中巻と分布巻，全節巻と短節巻とに分けられます。

①集中巻と分布巻
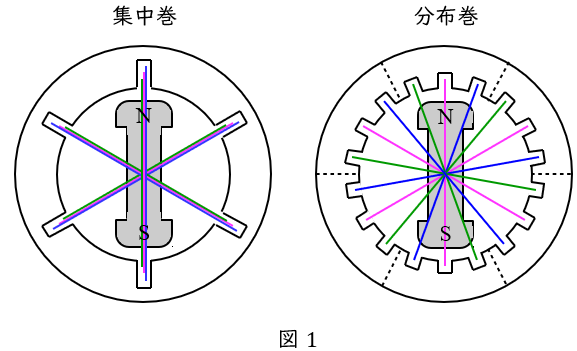
図1のような相数\( \ 3 \ \)の\( \ 2 \ \)極機の同期発電機について考えます。
集中巻は電機子巻線を一つのスロットに集中して巻き付ける巻線方式で，それぞれの起電力の向きが同じ向きであるため大きな起電力が得られることになりますが，奇数次の高調波を含むようになるため，磁束密度の分布が台形に近い形になってしまいます。
一方，分布巻は電機子巻線を複数のスロットに巻き付ける巻線方式で，電機子巻線に発生する誘導起電力の波形を正弦波に近づけることができるようになります。合成の起電力はそれぞれの巻線の起電力の向きが異なるため，それぞれの起電力のベクトル和となり，集中巻と比べて小さくなります。

②全節巻と短節巻
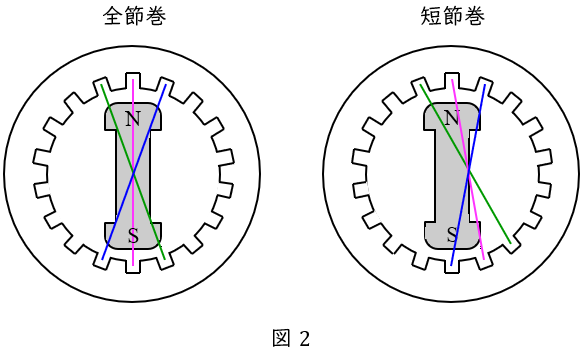
図2のように，\( \ 1 \ \)相分の巻線について，全節巻と短節巻の違いを示します。
全節巻では，コイルの間隔を\( \ \pi \ \mathrm {[rad]} \ \)として，短節巻ではコイルの間隔を\( \ \pi \ \mathrm {[rad]} \ \)より小さくして配置します。
短節巻の方がコイルの起電力は小さくなりますが，電機子巻線に発生する誘導起電力は正弦波に近づけることができるようになります。

2.等比数列の和（数学）
初項が\( \ a \ \)，公比が\( \ r \ \)の等比数列，
\[
\begin{eqnarray}
a，ar，ar^{2}，\cdots ，ar^{n-1} \\[ 5pt ] \end{eqnarray}
\] があるときその和\( \ S_{\mathrm {n}} \ \)は，
\[
\begin{eqnarray}
S_{\mathrm {n}}&=&a+ar+ar^{2}+\cdots +ar^{n-1} \ 　・・・・・・・・・・　①　\\[ 5pt ] \end{eqnarray}
\] となります。両辺\( \ r \ \)倍すると，
\[
\begin{eqnarray}
rS_{\mathrm {n}}&=&ar+ar^{2}+ar^{3}+\cdots +ar^{n}　・・・・・・・・・・　②　 \\[ 5pt ] \end{eqnarray}
\] となるので，\( \ ①-② \ \)より，
\[
\begin{eqnarray}
\left( 1-r\right) S_{\mathrm {n}}&=&a-ar^{n}　\\[ 5pt ] S_{\mathrm {n}}&=&\frac {a\left( 1-r^{n}\right) }{1-r}　\\[ 5pt ] \end{eqnarray}
\] で求められます。\( \ r ＜ 1 \ \)であると仮定して\( \ n → \infty \ \)であるとすると，
\[
\begin{eqnarray}
S_{\infty}&=&\frac {a}{1-r}　\\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ハ
題意より解答候補は，（ロ）三角，（ハ）方形，（ホ）のこぎり，になると思います。
ワンポイント解説「1.同期発電機のコイルの巻き方の違い」の通り，集中巻の場合，起磁力の空間分布は方形波となります。

(2)解答：ヘ
題意より解答候補は，（イ）実数，（ニ）偶数，（ヘ）奇数，になると思います。
ワンポイント解説「1.同期発電機のコイルの巻き方の違い」の通り，集中巻の場合，奇数次の空間高調波起磁力も生じることになります。

(3)解答：カ
題意より，合成起磁力ベクトル\( \ \dot F \ \)は，初項\( \ f \ \)，公比\( \ e^{-j\alpha } \ \)の等比級数であるから，ワンポイント解説「2.等比数列の和（数学）」の通り，
\[
\begin{eqnarray}
\dot F&=&f\frac {1-e^{-jq\alpha }}{1-e^{-j\alpha }}　\\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
オイラーの公式\( \ e^{-j\theta }=\cos \theta -j\sin \theta \ \)より，\( \ \left| 1-e^{-jq\alpha }\right| \ \)は，
\[
\begin{eqnarray}
\left| 1-e^{-jq\alpha }\right| &=&\left| 1-\left( \cos q\alpha -j\sin q\alpha \right) \right|　\\[ 5pt ] &=&\left| 1-\cos q\alpha +j\sin q\alpha \right|　\\[ 5pt ] &=&\sqrt {\left( 1-\cos q\alpha \right) ^{2} +\sin ^{2} q\alpha }　\\[ 5pt ] &=&\sqrt {1-2\cos q\alpha +\cos ^{2} q\alpha +\sin ^{2} q\alpha }　\\[ 5pt ] &=&\sqrt {1-2\cos q\alpha +1}　\\[ 5pt ] &=&\sqrt {2-2\cos q\alpha }　\\[ 5pt ] \end{eqnarray}
\] となり，半角の公式\( \ \displaystyle \sin ^{2} \theta =\frac {1-\cos 2\theta }{2} \ \)より，
\[
\begin{eqnarray}
\left| 1-e^{-jq\alpha }\right| &=&\sqrt {2-2\cos q\alpha }　\\[ 5pt ] &=&\sqrt {4\cdot \frac {1-\cos q\alpha }{2}}　\\[ 5pt ] &=&\sqrt {4\sin ^{2} \left( \frac {q\alpha }{2}\right) }　\\[ 5pt ] &=&2\sin \left( \frac {q\alpha }{2}\right) \\[ 5pt ] \end{eqnarray}
\] となる。同様に，\( \ \displaystyle \left| 1-e^{-j\alpha }\right| =2\sin \left( \frac {\alpha }{2}\right) \ \)となるから，
\[
\begin{eqnarray}
F&=&\left| f\frac {1-e^{-jq\alpha }}{1-e^{-j\alpha }} \right| \\[ 5pt ] &=&f\frac {\displaystyle 2\sin \left( \frac {q\alpha }{2}\right) }{\displaystyle 2\sin \left( \frac {\alpha }{2}\right) } \\[ 5pt ] &=&f\frac {\displaystyle \sin \left( \frac {q\alpha }{2}\right) }{\displaystyle \sin \left( \frac {\alpha }{2}\right) } \\[ 5pt ] \end{eqnarray}
\] となるので，分布係数\( \ k_{d1} \ \)は，
\[
\begin{eqnarray}
k_{d1}&=&\frac {F}{qf} \\[ 5pt ] &=&\frac {\displaystyle f\frac {\displaystyle \sin \left( \frac {q\alpha }{2}\right) }{\displaystyle \sin \left( \frac {\alpha }{2}\right) }}{qf} \\[ 5pt ] &=&\frac {\displaystyle \sin \left( \frac {q\alpha }{2}\right) }{\displaystyle q\sin \left( \frac {\alpha }{2}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：リ
第\( \ n \ \)次空間高調波に対する分布係数\( \ k_{dn} \ \)は，(4)解答式を\( \ \alpha → n\alpha \ \)とすれば良いので，
\[
\begin{eqnarray}
k_{dn}&=&\frac {\displaystyle \sin \left( \frac {qn\alpha }{2}\right) }{\displaystyle q\sin \left( \frac {n\alpha }{2}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。