【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,点電荷による直交する\( \ 2 \ \)枚の接地導体上の誘導電荷密度に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
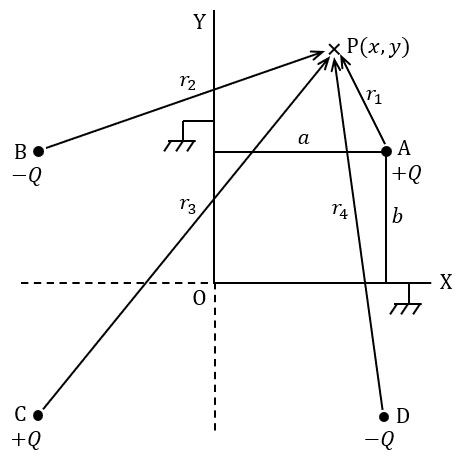
互いに直交している\( \ 2 \ \)枚の無限に広い導体平面を接地し,図のように\( \ \mathrm {O} \ \)を原点とした\( \ \mathrm {XY} \ \)二次元座標\( \ (a, b) \ \)の点\( \ \mathrm {A} \ \)に点電荷\( \ +Q \ \)を置いたとき,導体平面の\( \ \mathrm {OX} \ \)及び\( \ \mathrm {OY} \ \)軸上の誘導電荷密度を求めてみよう。
点\( \ \mathrm {A} \ \)に点電荷\( \ +Q \ \)を置くとき,導体平面上の\( \ \mathrm {OY} \ \),\( \ \mathrm {OX} \ \)に関する点\( \ \mathrm {A} \ \)の鏡像になる点\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)及び\( \ \mathrm {D} \ \)にはそれぞれ\( \ -Q \ \),\( \ +Q \ \)及び\( \ -Q \ \)の点電荷が存在しているとみなして誘導電荷密度を計算することができる。したがって,\( \ \mathrm {XY} \ \)二次元平面上の任意の点\( \ \mathrm {P} (x, y) \ \)の電位\( \ V \ \)は\( \ \fbox { (1) } \ \)となる。また,そこでの電界\( \ E \ \)の\( \ x \ \)軸方向成分\( \ E_{x} \ \),\( \ y \ \)軸方向成分\( \ E_{y} \ \)はそれぞれ\( \ \fbox { (2) } \ \)として求められる。そこで,導体平面の\( \ \mathrm {OX} \ \)軸上の誘導電荷密度\( \ \sigma _{x} \ \)並びに\( \ \mathrm {OY} \ \)軸上の誘導電荷密度\( \ \sigma _{y} \ \)は\( \ \fbox { (2) } \ \)を使って\( \ \fbox { (3) } \ \)として計算される。ところで,導体平面の\( \ \mathrm {OX} \ \)軸上では\( \ r_{1}=r_{4} \ \),\( \ r_{2}=r_{3} \ \)であることに注目すれば,\( \ \mathrm {OX} \ \)軸上の誘導電荷密度\( \ \sigma _{x} \ \)は\( \ \fbox { (4) } \ \)となる。例えば,導体平面の\( \ \mathrm {OX} \ \)軸上で点\( \ \mathrm {A} \ \)の真下の点\( \ (a, 0) \ \)の誘導電荷密度は\( \ \fbox { (5) } \ \)と計算される。ただし,導体の置かれている空間の誘電率を\( \ \varepsilon \ \)とする。また,\( \ r_{1}=\sqrt {\left( x-a\right) ^{2}+\left( y-b\right) ^{2} } \ \),\( \ r_{2}=\sqrt {\left( x+a\right) ^{2}+\left( y-b\right) ^{2} } \ \),\( \ r_{3}=\sqrt {\left( x+a\right) ^{2}+\left( y+b\right) ^{2} } \ \),\( \ r_{4}=\sqrt {\left( x-a\right) ^{2}+\left( y+b\right) ^{2} } \ \)とする。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {bQ}{2\pi }\left[ \frac {1}{b^{3}}-\frac {1}{\left( \sqrt {4a^{2}+b^{2}}\right) ^{3}}\right] &(ロ)& E_{x}=-\frac{ \partial V }{ \partial x },E_{y}=-\frac{ \partial V }{ \partial y } \\[ 5pt ]
&(ハ)& \frac {Q}{4\pi \varepsilon }\left( \frac {1}{r_{1}}-\frac {1}{r_{2}}+\frac {1}{r_{3}}-\frac {1}{r_{4}}\right) &(ニ)& \sigma _{x}=\varepsilon \left( \frac{ \partial V }{ \partial y }\right) _{y=0},\sigma _{y}=\varepsilon \left( \frac{ \partial V }{ \partial x }\right) _{x=0} \\[ 5pt ]
&(ホ)& -\frac {bQ}{2\pi }\left( \frac {1}{{r_{1}}^{3}}-\frac {1}{{r_{2}}^{3}}\right) &(ヘ)& E_{x}=-\frac{ \partial V }{ \partial y },E_{y}=-\frac{ \partial V }{ \partial x } \\[ 5pt ]
&(ト)& \sigma _{x}=-\varepsilon \left( \frac{ \partial V }{ \partial x }\right) _{y=0},\sigma _{y}=-\varepsilon \left( \frac{ \partial V }{ \partial y }\right) _{x=0} &(チ)& \frac {Q^{2}}{4\pi \varepsilon }\left( \frac {1}{r_{1}}-\frac {1}{r_{2}}+\frac {1}{r_{3}}-\frac {1}{r_{4}}\right) \\[ 5pt ]
&(リ)& -\frac {bQ}{2\pi }\left[ \frac {1}{b^{3}}-\frac {1}{\left( \sqrt {4a^{2}+b^{2}}\right) ^{3}}\right] &(ヌ)& \frac {bQ}{2\pi }\left( \frac {1}{{r_{1}}^{3}}-\frac {1}{{r_{2}}^{3}}\right) \\[ 5pt ]
&(ル)& \sigma _{x}=-\varepsilon \left( \frac{ \partial V }{ \partial y }\right) _{y=0},\sigma _{y}=-\varepsilon \left( \frac{ \partial V }{ \partial x }\right) _{x=0} &(ヲ)& E_{x}=\frac{ \partial V }{ \partial x },E_{y}=\frac{ \partial V }{ \partial y } \\[ 5pt ]
&(ワ)& -\frac {bQ}{2\pi \varepsilon }\left[ \frac {1}{b^{3}}-\frac {1}{\left( \sqrt {4a^{2}+b^{2}}\right) ^{3}}\right] &(カ)& -\frac {bQ}{2\pi \varepsilon }\left( \frac {1}{{r_{1}}^{3}}-\frac {1}{{r_{2}}^{3}}\right) \\[ 5pt ]
&(ヨ)& \frac {Q}{4\pi \varepsilon }\left( \frac {1}{{r_{1}}^{2}}-\frac {1}{{r_{2}}^{2}}+\frac {1}{{r_{3}}^{2}}-\frac {1}{{r_{4}}^{2}}\right) && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
点電荷による\( \ 2 \ \)枚の接地導体上の誘導電荷密度を求める問題です。
条件は比較的単純ですが,(4)からの計算量が多くさすが\( \ 1 \ \)種らしい問題と言えると思います。他の問題がスムーズに進み残りがこの問題のみであれば問題ありませんが,時間が足りない場合には,例え解けそうと思っても捨てる勇気も重要です。
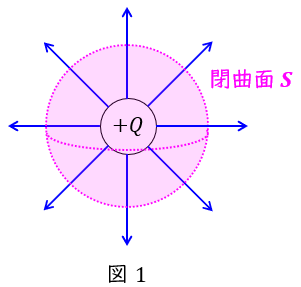
1.ガウスの法則
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの法則といいます。閉曲面が球で,点電荷に蓄えられている電荷\( \ Q \ \mathrm {[C]} \ \)があれば,電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
4\pi r^{2} \cdot E &=& \frac {Q}{\varepsilon } \\[ 5pt ]
E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
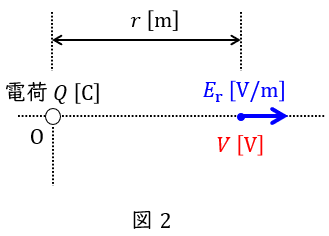
2.空間上の電位\( \ V \ \)
中心からの距離\( \ r \ \mathrm {[m]} \ \)に関する電界\( \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ \)が与えられている時,その場所の電位\( \ V \ \mathrm {[V]} \ \)は無限遠を基準とすると,
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ]
\end{eqnarray}
\]
で求められます。仮に図2のように,誘電率が\( \ \varepsilon \ \mathrm {[F / m]} \ \)の空間に電荷\( \ Q \ \mathrm {[C]} \ \)の電荷があるとき,\( \ r \ \mathrm {[m]} \ \)離れた場所の電位\( \ V \ \mathrm {[V]} \ \)は
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}\frac {Q}{4\pi \varepsilon r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon }\int _{\infty }^{r}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon }\left[ -\frac {1}{r}\right] _{\infty }^{r} \\[ 5pt ]
&=&-\frac {Q}{4\pi \varepsilon }\left( -\frac {1}{r}\right) \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.空間中の電束密度の大きさ
真空中に電荷\( \ Q \ \mathrm {[C]} \ \)をおいた時,電荷から距離\( \ r \ \mathrm {[m]} \ \)離れた場所の電束密度の大きさ\( \ D \ \mathrm {[C / m^{2}]} \ \)は,ガウスの法則より,
\[
\begin{eqnarray}
D &=&\frac {Q}{4\pi r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。空間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると,電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。
【解答】
(1)解答:ハ
電位はスカラー量であり,点\( \ \mathrm {P} (x, y) \ \)の電位\( \ V \ \)はそれぞれの電荷による電位のスカラー和となるので,ワンポイント解説「2.空間上の電位\( \ V \ \)」の通り,
\[
\begin{eqnarray}
V&=&\frac {Q}{4\pi \varepsilon r_{1}}-\frac {Q}{4\pi \varepsilon r_{2}}+\frac {Q}{4\pi \varepsilon r_{3}}-\frac {Q}{4\pi \varepsilon r_{4}} \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon }\left( \frac {1}{r_{1}}-\frac {1}{r_{2}}+\frac {1}{r_{3}}-\frac {1}{r_{4}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ロ
ワンポイント解説「2.空間上の電位\( \ V \ \)」より,電位\( \ V \ \)は電界\( \ E \ \)の積分,すなわち電界\( \ E \ \)は電位\( \ V \ \)の微分であるので,その\( \ x \ \)軸方向成分\( \ E_{x} \ \)及び\( \ y \ \)軸方向成分\( \ E_{y} \ \)はそれぞれ\( \ \displaystyle E_{x}=-\frac{ \partial V }{ \partial x },E_{y}=-\frac{ \partial V }{ \partial y } \ \)と求められる。
(3)解答:ル
導体平面の\( \ \mathrm {OX} \ \)軸上の誘導電荷密度\( \ \sigma _{x} \ \)は\( \ y=0 \ \)の場所における誘導電荷密度であり,その大きさは電束密度と等しい。\( \ \mathrm {OX} \ \)軸上の電束密度は垂直方向なので,ワンポイント解説「3.空間中の電束密度の大きさ」の通り,
\[
\begin{eqnarray}
\sigma _{x}&=&\left( \varepsilon E _{y} \right) _{y=0} \\[ 5pt ]
&=&-\varepsilon \left( \frac{ \partial V }{ \partial y }\right) _{y=0} \\[ 5pt ]
\end{eqnarray}
\]
となり,同様に,
\[
\begin{eqnarray}
\sigma _{y}&=&\left( \varepsilon E _{x} \right) _{x=0} \\[ 5pt ]
&=&-\varepsilon \left( \frac{ \partial V }{ \partial x }\right) _{x=0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ホ
(1)解答式に\( \ r_{1}=\sqrt {\left( x-a\right) ^{2}+\left( y-b\right) ^{2} } \ \),\( \ r_{2}=\sqrt {\left( x+a\right) ^{2}+\left( y-b\right) ^{2} } \ \),\( \ r_{3}=\sqrt {\left( x+a\right) ^{2}+\left( y+b\right) ^{2} } \ \),\( \ r_{4}=\sqrt {\left( x-a\right) ^{2}+\left( y+b\right) ^{2} } \ \)を代入すると,
\[
\begin{eqnarray}
V&=&\frac {Q}{4\pi \varepsilon }\left( \frac {1}{\sqrt {\left( x-a\right) ^{2}+\left( y-b\right) ^{2} }}-\frac {1}{\sqrt {\left( x+a\right) ^{2}+\left( y-b\right) ^{2} }}+\frac {1}{\sqrt {\left( x+a\right) ^{2}+\left( y+b\right) ^{2} }}-\frac {1}{\sqrt {\left( x-a\right) ^{2}+\left( y+b\right) ^{2} }}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ A=y-b \ \),\( \ B=\left( x-a\right) ^{2}+A ^{2} \ \),\( \ \displaystyle C=\frac {1}{\sqrt {B}}=\frac {1}{\sqrt {\left( x-a\right) ^{2}+\left( y-b\right) ^{2} }} \ \)とおけば,
\[
\begin{eqnarray}
\frac{ \partial C}{ \partial y } &=&\frac { \partial C}{ \partial B }\cdot \frac { \partial B}{ \partial A }\cdot \frac { \partial A}{ \partial y } \\[ 5pt ]
&=&-\frac {1}{2}\frac {1}{\sqrt {B^{3}}}\cdot 2A\cdot 1 \\[ 5pt ]
&=&-\frac {A}{\sqrt {B^{3}}} \\[ 5pt ]
&=&-\frac {y-b}{\sqrt {\left\{ \left( x-a\right) ^{2}+A ^{2}\right\} ^{3}}} \\[ 5pt ]
&=&-\frac {y-b}{\sqrt {\left\{ \left( x-a\right) ^{2}+\left( y-b\right) ^{2}\right\} ^{3}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。同様に各項も計算できるので,
\[
\begin{eqnarray}
\frac{ \partial V}{ \partial y } &=&\frac {Q}{4\pi \varepsilon }\left[ -\frac {y-b}{\sqrt {\left\{ \left( x-a\right) ^{2}+\left( y-b\right) ^{2}\right\} ^{3}}}+\frac {y-b}{\sqrt {\left\{ \left( x+a\right) ^{2}+\left( y-b\right) ^{2}\right\} ^{3}}}-\frac {y+b}{\sqrt {\left\{ \left( x+a\right) ^{2}+\left( y+b\right) ^{2}\right\} ^{3}}}+\frac {y+b}{\sqrt {\left\{ \left( x-a\right) ^{2}+\left( y+b\right) ^{2}\right\} ^{3}}}\right] \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ y=0 \ \)を代入すれば,
\[
\begin{eqnarray}
\left( \frac{ \partial V}{ \partial y }\right) _{y=0} &=&\frac {Q}{4\pi \varepsilon }\left[ -\frac {0-b}{\sqrt {\left\{ \left( x-a\right) ^{2}+\left( 0-b\right) ^{2}\right\} ^{3}}}+\frac {0-b}{\sqrt {\left\{ \left( x+a\right) ^{2}+\left( 0-b\right) ^{2}\right\} ^{3}}}-\frac {0+b}{\sqrt {\left\{ \left( x+a\right) ^{2}+\left( 0+b\right) ^{2}\right\} ^{3}}}+\frac {0+b}{\sqrt {\left\{ \left( x-a\right) ^{2}+\left( 0+b\right) ^{2}\right\} ^{3}}}\right] \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon }\left[ \frac {b}{\sqrt {\left\{ \left( x-a\right) ^{2}+b^{2}\right\} ^{3}}}-\frac {b}{\sqrt {\left\{ \left( x+a\right) ^{2}+b^{2}\right\} ^{3}}}-\frac {b}{\sqrt {\left\{ \left( x+a\right) ^{2}+b^{2}\right\} ^{3}}}+\frac {b}{\sqrt {\left\{ \left( x-a\right) ^{2}+b^{2}\right\} ^{3}}}\right] \\[ 5pt ]
&=&\frac {Q}{4\pi \varepsilon }\left[ \frac {2b}{\sqrt {\left\{ \left( x-a\right) ^{2}+b^{2}\right\} ^{3}}}-\frac {2b}{\sqrt {\left\{ \left( x+a\right) ^{2}+b^{2}\right\} ^{3}}}\right] \\[ 5pt ]
&=&\frac {bQ}{2\pi \varepsilon }\left( \frac {1}{{r_{1}}^{3}}-\frac {1}{{r_{2}}^{3}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ \mathrm {OX} \ \)軸上の誘導電荷密度\( \ \sigma _{x} \ \)は,
\[
\begin{eqnarray}
\sigma _{x}&=&-\varepsilon \left( \frac{ \partial V }{ \partial y }\right) _{y=0} \\[ 5pt ]
&=&-\frac {bQ}{2\pi }\left( \frac {1}{{r_{1}}^{3}}-\frac {1}{{r_{2}}^{3}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:リ
点\( \ \mathrm {A} \ \)の真下の点\( \ (a, 0) \ \)において,
\[
\begin{eqnarray}
r_{1}&=&\sqrt {\left( x-a\right) ^{2}+\left( y-b\right) ^{2} } \\[ 5pt ]
&=&\sqrt {\left( a-a\right) ^{2}+\left( 0-b\right) ^{2} } \\[ 5pt ]
&=&b \\[ 5pt ]
r_{2}&=&\sqrt {\left( x+a\right) ^{2}+\left( y-b\right) ^{2} } \\[ 5pt ]
&=&\sqrt {\left( a+a\right) ^{2}+\left( 0-b\right) ^{2} } \\[ 5pt ]
&=&\sqrt {4a^{2}+b^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,誘導電荷密度\( \ \sigma _{x} \ \)は,
\[
\begin{eqnarray}
\sigma _{x}&=&-\frac {bQ}{2\pi }\left( \frac {1}{{r_{1}}^{3}}-\frac {1}{{r_{2}}^{3}}\right) \\[ 5pt ]
&=&-\frac {bQ}{2\pi }\left[ \frac {1}{b^{3}}-\frac {1}{\left( \sqrt {4a^{2}+b^{2}}\right) ^{3}}\right] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん