【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,水力発電所の設計手順に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
\( 1. \ \)計画地点の発電所の諸元データ(発電所型式,使用水量,有効落差など)を得る。
\( 2. \ \)有効落差\( \ \mathrm {[m]} \ \),使用水量\( \ \mathrm {[m^{3} / s]} \ \)から次式で与えられる発電所の\( \ \fbox { (1) } \ \mathrm {[kW]} \ \)を算出する。
\[
\begin{eqnarray}
\ \fbox { (1) } \ &=& 9.8 \times 使用水量\times 有効落差 \\[ 5pt ]
\end{eqnarray}
\]
\( 3. \ \)\( \ \fbox { (1) } \ \)と有効落差から型式選定図などを用いて,\( \ \fbox { (2) } \ \)を選定する。
\( 4. \ \)仮水車出力\( \ P \ \mathrm {[kW]} \ \)を算出する。
\[
\begin{eqnarray}
仮水車出力P &=& 9.8\times 使用水量\times 有効落差 \times 水車効率 \\[ 5pt ]
\end{eqnarray}
\]
(水車効率は,予想される最高効率を用いる。)
\( 5. \ \)有効落差\( \ H \ \mathrm {[m]} \ \)から水車の\( \ \fbox { (3) } \ \)の限界を算出する。
例えば,フランシス水車の場合,
\[
\begin{eqnarray}
\ \fbox { (3) } \ &≦& 21 \ 000 / (H+25) +35 \\[ 5pt ]
\end{eqnarray}
\]
\( 6. \ \)回転速度\( \ \mathrm {[{min}^{-1}]} \ \)の限界を求める。
\[
\begin{eqnarray}
回転速度 &=& \ \fbox { (3) } \ \times H^{ \ \fbox { (4) } \ } / P^{\frac {1}{2}} \\[ 5pt ]
\end{eqnarray}
\]
\( 7. \ \)次式から前述の回転速度の限界以下となる同期の回転速度\( \ \mathrm {[{min}^{-1}]} \ \)を選定する。
\[
\begin{eqnarray}
回転速度 &=& 120f / p \\[ 5pt ]
\end{eqnarray}
\]
(ここで,\( \ f \ \):周波数,\( \ p \ \):発電機極数)
\( 8. \ \)水車の「出力-効率曲線」から水車効率を求め,発電機の「負荷-効率曲線」から発電機効率を求める。
\( 9. \ \)得られた効率特性から,水車出力,発電機容量などを決定する。
\( 10. \ \)水車発電機の概略寸法,概略重量を算出し,発電所レイアウトを設計する。
\( 11. \ \)水車の設置レベルの決定に当たり,キャビテーション防止を考慮した\( \ \fbox { (5) } \ \)を水頭換算で算出する。
\[
\begin{eqnarray}
\ \fbox { (5) } \ &=& 大気圧(水頭換算値) -飽和蒸気圧(水頭換算値)-キャビテーション係数\times 有効落差 \\[ 5pt ]
\end{eqnarray}
\]
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 定格出力 &(ロ)& \frac {5}{4} &(ハ)& 発電出力 \\[ 5pt ]
&(ニ)& 運転方式 &(ホ)& 水車型式 &(ヘ)& 入口弁型式 \\[ 5pt ]
&(ト)& \frac {3}{4} &(チ)& 理論出力 &(リ)& 無拘束速度 \\[ 5pt ]
&(ヌ)& 吸出し高さ &(ル)& 取水口水位 &(ヲ)& 同期速度 \\[ 5pt ]
&(ワ)& 比速度 &(カ)& 放出口水位 &(ヨ)& \frac {4}{5} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
水力発電所の設計手順に関する問題です。
設計手順なので一見すると専門性が高く難易度も高そうな内容ですが,中身は水力発電所の設備や公式を理解していれば解けるように工夫されています。
わかりにくい空欄も消去法で解いていき高得点を目指すようにして下さい。
1.水力発電所の出力\( \ P \ \)
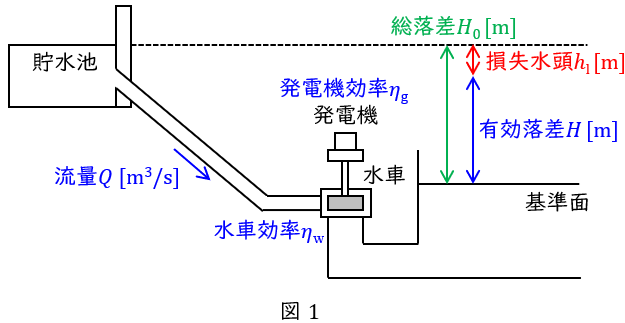
水力発電所の使用水量\( \ Q \ \mathrm {[m^{3}/s]} \ \),有効落差\( \ H \ \mathrm {[m]} \ \)とすると,理論水力\( \ P_{0} \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P_{0} &=&9.8QH \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となり,水車効率\( \ \eta _{\mathrm {w}} \ \),発電機効率\( \ \eta _{\mathrm {g}} \ \)とすると,発電機の出力\( \ P \ \mathrm {[kW]} \ \)は,
\[
\begin{eqnarray}
P &=&9.8QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。これは重力加速度\( \ g=9.8 \ \mathrm {[m/s^{2}]} \ \)及び水の密度\( \ \rho =1 \ 000 \ \mathrm {[kg/m^{3}]} \ \)を使用した時の発電機の出力である
\[
\begin{eqnarray}
P &=&\rho gQH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
に各値を代入し,
\[
\begin{eqnarray}
P &=&1 \ 000 \times 9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[W]} \\[ 5pt ]
&=&9.8 QH\eta _{\mathrm {w}}\eta _{\mathrm {g}} \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
として導出したものです。
2.比速度の定義
水車の形状を相似に保ったまま大きさを小さくし,\( \ 1 \ \mathrm {m} \ \)の有効落差で\( \ 1 \ \mathrm {kW} \ \)の出力を発生するときの回転速度を言います。定格回転数を\( \ n \ \mathrm {[min^{-1}]} \ \),水車の出力を\( \ P \ \mathrm {[kW]} \ \),有効落差を\( \ H \ \mathrm {[m]} \ \)とすると,比速度\( \ n_{\mathrm {s}} \ \mathrm {[m\cdot kW]} \ \)は,
\[
\begin{eqnarray}
n_{\mathrm {s}} &=&n \cdot \frac {\displaystyle P^{\frac {1}{2}}}{\displaystyle H^{\frac {5}{4}}} \\[ 5pt ]
\end{eqnarray}
\]
となります。なお,経験則として比速度には上限値が\( \ \mathrm {JEC} \ \)で定められており,フランシス水車においては以下の式となっています。(原則暗記不要。改定の可能性あり。)
\[
\begin{eqnarray}
n_{\mathrm {s}} &≦&\frac {21 \ 000}{H+25}+35 \\[ 5pt ]
\end{eqnarray}
\]
3.各水車の落差と比速度の関係
各水車の落差と比速度の関係は下表の通りとなり,一般に高落差の物ほど比速度は小さくなります。
\[
\begin{array}{|c|c|c|}
\hline
& 落差 \ \mathrm {[m]} & 比速度 \ \mathrm {[m\cdot kW]} \\
\hline
ペルトン水車 & 150 ~ 800 & 小 \\
\hline
フランシス水車 & 40 ~ 500 & 小~中 \\
\hline
{\displaystyle 斜流水車}\atop {\displaystyle (デリア水車)} & 40 ~ 180 & 中~大 \\
\hline
{\displaystyle プロペラ水車}\atop {\displaystyle (カプラン水車)} & 5 ~ 80 & 中~大 \\
\hline
\end{array}
\]
4.三相同期発電機の同期速度\( \ N_{\mathrm {s}} \ \)
三相同期発電機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。同期機は同期速度で回転します。
5.吸出し管
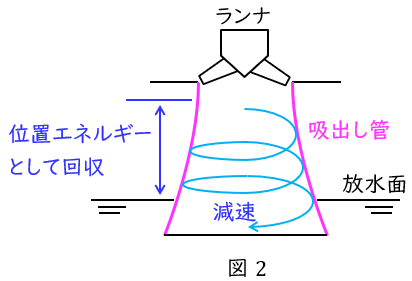
フランシス水車をはじめとする水が充満されている反動水車の出口に設けられる管で,図2に示すようなラッパ状の形をしたものが一般的です。
ランナで仕事をした水をそのまま放水口に出すのではなく,ランナから出た水の流路を広げランナ出口の圧力を大気圧以下に保持し,ラッパ状に広げ流速を落とすことで運動エネルギーを位置エネルギーとして回収します。
理論上の吸出し管の高さは大気圧(1気圧)である約\( \ 10.33 \ \mathrm {m} \ \)までですが,実際にはキャビテーション発生防止のため\( \ 7 \ \mathrm {m} \ \)程度までとしています。
【解答】
(1)解答:チ
題意より解答候補は,(イ)定格出力,(ハ)発電出力,(チ)理論出力,になると思います。
ワンポイント解説「1.水力発電所の出力\( \ P \ \)」の通り,有効落差\( \ \mathrm {[m]} \ \),使用水量\( \ \mathrm {[m / s]} \ \)から与えられる式は理論出力となります。
(2)解答:ホ
題意より解答候補は,(ニ)運転方式,(ホ)水車型式,(ヘ)入口弁型式,になると思います。
ワンポイント解説「3.各水車の落差と比速度の関係」の通り,理論出力と有効落差から選定するのは水車型式が最も適当となります。
(3)解答:ワ
題意より解答候補は,(リ)無拘束速度,(ヲ)同期速度,(ワ)比速度,になると思います。
ワンポイント解説「2.比速度の定義」の通り,有効落差から算出するのは比速度の限界でフランシス水車の場合は,比速度\( \ ≦ 21 \ 000 / (H+25) +35 \ \)となります。
(4)解答:ロ
題意より解答候補は,(ロ)\( \ \displaystyle \frac {5}{4} \ \),(ト)\( \ \displaystyle \frac {3}{4} \ \),(ヨ)\( \ \displaystyle \frac {4}{5} \ \),になると思います。
ワンポイント解説「2.比速度の定義」の通り,比速度と回転速度の関係は,
\[
\begin{eqnarray}
回転速度 &=& 比速度 \ \times H^{ \frac {5}{4} } / P^{\frac {1}{2}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
(5)解答:ヌ
題意より解答候補は,(ヌ)吸出し高さ,(ル)取水口水位,(カ)放出口水位,になると思います。
ワンポイント解説「5.吸出し管」の通り,水車の設置レベルの決定に当たり,キャビテーション防止を考慮した吸出し高さを算定します。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん