【問題】
【難易度】★★★☆☆(普通)
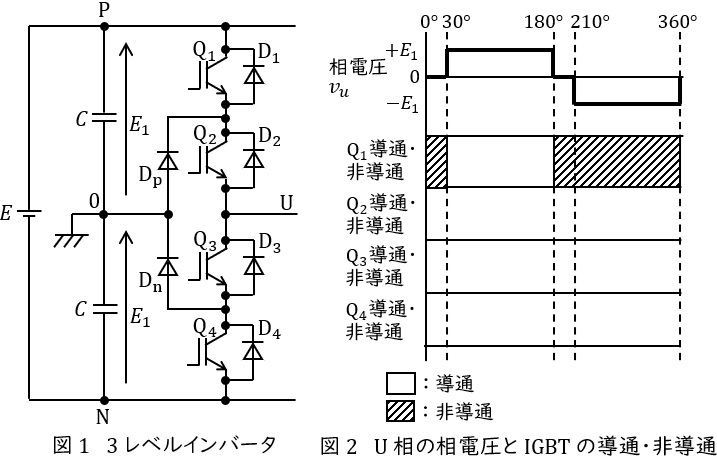
図1には\( \ \mathrm {IGBT} \ \)を用いた三相出力\( \ 3 \ \)レベルインバータの\( \ \mathrm {U} \ \)相分を示す。直流電源のプラス電位,中性点電位及びマイナス電位の三つを出力できることからその名前が付けられ,近年多くの用途に用いられるようになった。\( \ \mathrm {IGBT} \ \)のスイッチング時サージ電圧及びデッドタイムを無視した理想的なインバータとしたとき,次の問に答えよ。
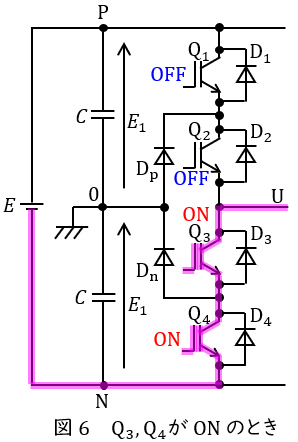
(1) 図1の\( \ 3 \ \)レベルインバータにおいて,プラス電位,中性点電位及びマイナス電位の三つの電位を出力するそれぞれのときに導通するパワーデバイスはどれか。
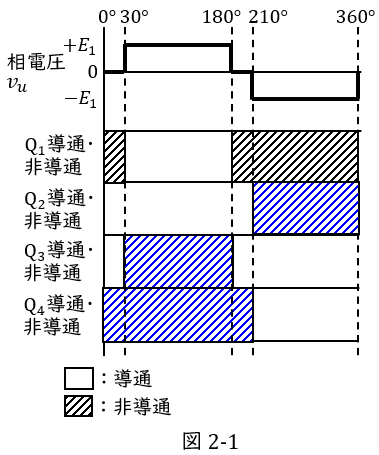
(2) 直流電源の中間点を零電位とした場合,図2に\( \ \mathrm {U} \ \)相の相電圧を示す。図2を答案用紙に写し取り,\( \ \mathrm {Q_{1}} \ \)の例にならって,\( \ \mathrm {Q_{2}} \ \),\( \ \mathrm {Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が導通・非道通の期間を\( \ 1 \ \)サイクルにわたって示せ。なお,\( \ \mathrm {Q_{1}} \ \)の\( \ \mathrm {IGBT} \ \)は\( \ 30^{\circ }\sim 180^{\circ } \ \)で導通,\( \ 0^{\circ }\sim 30^{\circ } \ \)と\( \ 180^{\circ }\sim 360^{\circ } \ \)で非導通であるので,図2には例として,導通期間を空白のまま,非導通期間をハッチングで示している。
(3) 上記(2)の相電圧波形の実効値を求めよ。
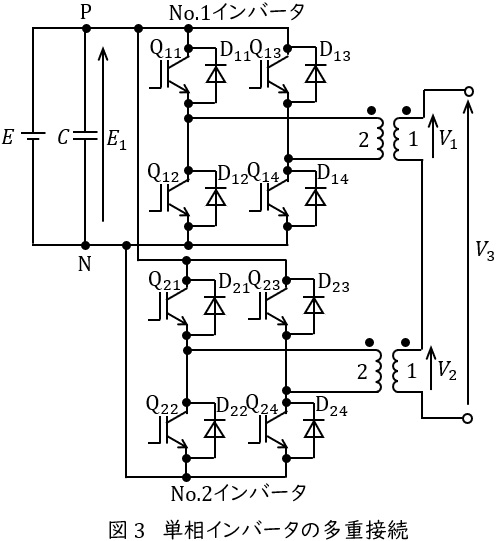
(4) 図3には,\( \ \mathrm {IGBT} \ \)を用いた単相インバータの多重接続によって三相出力インバータの一相分を実現している例を示す。\( \ 3 \ \)レベルインバータと同様に出力波形を改善できる回路構成であるが,始動あるいは零速度運転を含む広い可変速範囲で,大容量電動機を駆動する用途には\( \ 3 \ \)レベルインバータが使われることが多い。その理由を述べよ。
【ワンポイント解説】
\( \ 3 \ \)レベルインバータの動作と出力電圧に関する問題です。
(4)は難易度が高いですが,(3)までは比較的取り組みやすい問題です。(3)まで正答できれば十分合格圏内となりますので,(3)までは確実に解けるようになりましょう。
1.単相\( \ 3 \ \)レベルインバータの動作
本問の単相\( \ 3 \ \)レベルインバータは,\( \ \mathrm {Q_{1}} \ \)~\( \ \mathrm {Q_{4}} \ \)をオンオフ制御することで,以下の\( \ 3 \ \)パターンの電圧を出力し,交流を得ることができるインバータです。
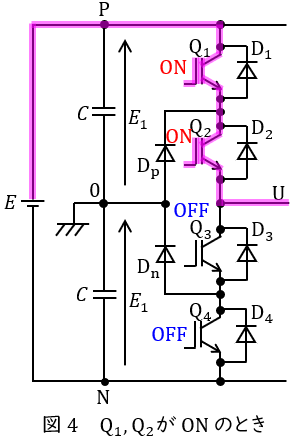
① \( \ \mathrm {Q_{1}} \ \)と\( \ \mathrm {Q_{2}} \ \)が\( \ \mathrm {ON} \ \),\( \ \mathrm {Q_{3}} \ \)と\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {OFF} \ \)
図4のように導通するため,端子\( \ \mathrm {U} \ \)には正の電圧\( \ E_{1} \ \)が加わり,電位は\( \ v_{\mathrm {U}}=E_{1} \ \)となります。
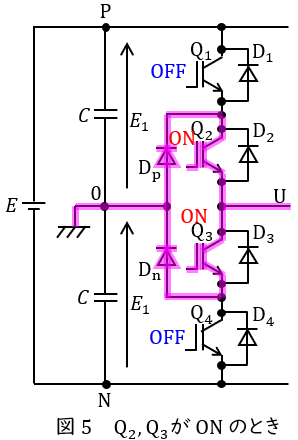
② \( \ \mathrm {Q_{2}} \ \)と\( \ \mathrm {Q_{3}} \ \)が\( \ \mathrm {ON} \ \),\( \ \mathrm {Q_{1}} \ \)と\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {OFF} \ \)
図5のように導通するため,端子\( \ \mathrm {U} \ \)の電位は\( \ v_{\mathrm {U}}=0 \ \)となります。
③ \( \ \mathrm {Q_{3}} \ \)と\( \ \mathrm {Q_{4}} \ \)が\( \ \mathrm {ON} \ \),\( \ \mathrm {Q_{1}} \ \)と\( \ \mathrm {Q_{2}} \ \)が\( \ \mathrm {OFF} \ \)
図6のように導通するため,端子\( \ \mathrm {U} \ \)には負の電圧\( \ -E_{1} \ \)が加わり,電位は\( \ v_{\mathrm {U}}=-E_{1} \ \)となります。
2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき,平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は,
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
E_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }E_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ]
&=&\frac {2}{\pi }E_{\mathrm {m}}
\end{eqnarray}
\]
となります。
②実効値\( \ F \ \)
定義式は,
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ]
\end{eqnarray}
\]
であり,これを正弦波\( \ e\left( t \right) =E_{\mathrm {m}}\sin \omega t \ \)に適用すると,
\[
\begin{eqnarray}
E &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{E_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ]
&=&E_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ]
&=&\frac {E_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\]
となります。
【解答】
(1)プラス電位,中性点電位及びマイナス電位の三つの電位を出力するそれぞれのときに導通するパワーデバイス
(ポイント)
・ワンポイント解説「1.単相\( \ 3 \ \)レベルインバータの動作」の通りです。
(試験センター解答例)
プラス電位では\( \ \mathrm {Q_{1}} \ \)と\( \ \mathrm {Q_{2}} \ \),中性点電位では\( \ \mathrm {Q_{2}} \ \)と\( \ \mathrm {Q_{3}} \ \),マイナス電位では\( \ \mathrm {Q_{3}} \ \)と\( \ \mathrm {Q_{4}} \ \)が同時に導通する。
(2)\( \ \mathrm {Q_{2}} \ \),\( \ \mathrm {Q_{3}} \ \)及び\( \ \mathrm {Q_{4}} \ \)が導通・非道通の期間
プラス電位,中性点電位及びマイナス電位の各電位について導通するのは(1)の通りなので,図2-1に示す期間となる。
(3)(2)の相電圧波形の実効値
実効値は\( \ 0^{\circ }\sim 180^{\circ } \ \)の期間で考えれば良いので,その大きさ\( \ V_{U} \ \)は,ワンポイント解説「2.平均値と実効値の定義」の通り,
\[
\begin{eqnarray}
V_{U}&=&\sqrt {\frac {1}{\pi } \int _{\frac {\pi }{6}}^{\pi } {E_{1}} ^{2} \mathrm {d}\theta } \\[ 5pt ]
&=&E_{1}\sqrt {\frac {1}{\pi } \int _{\frac {\pi }{6}}^{\pi } 1 \mathrm {d}\theta } \\[ 5pt ]
&=&E_{1}\sqrt {\frac {1}{\pi } \left[ \theta \right] _{\frac {\pi }{6}}^{\pi } } \\[ 5pt ]
&=&E_{1}\sqrt {\frac {1}{\pi } \left( \pi -\frac {\pi }{6} \right) } \\[ 5pt ]
&=&\sqrt {\frac {5}{6}}E_{1} \\[ 5pt ]
&≒&0.913E_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)始動あるいは零速度運転を含む広い可変速範囲で,大容量電動機を駆動する用途に\( \ 3 \ \)レベルインバータが使われることが多い理由
(ポイント)
・出力変圧器は基本的に交流のみに使用でき,周波数が非常に小さい場合磁気飽和が発生しやすくなり,周波数が零の場合には使用することができません。
・通常のインバータの場合高電圧を取り出す場合出力変圧器が必要となり,重量・体積の分不利となります。
(試験センター解答例)
・単相インバータの多重接続において,電動機を始動あるいは零速度運転するときの出力変圧器の電圧周波数比は,電動機の定格回転速度の電圧周波数比に対して,抵抗による電圧降下分を補償する必要があるためにかなり大きくなる。したがって,出力変圧器が飽和しないように設計しなければならず,重量・体積が大きくなりコストが上昇する。また,出力周波数が完全に零の場合の運転では,出力変圧器は使用できない。\( \ 3 \ \)レベルインバータにはこのような出力変圧器がないため,広い可変速範囲の運転に有利である。
・\( \ 3 \ \)レベルインバータでは,出力波形を改善する効果は同等でありながら,出力変圧器を用いなくても直接高電圧(同じ定格電圧の\( \ \mathrm {IGBT} \ \)を使用する通常のインバータと比べて\( \ 2 \ \)倍の電圧)が出力できる。したがって,回路構成全体ではほぼ出力変圧器に相当する重量・体積分が小さくなって,大きな出力が達成できる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん