【問題】
【難易度】★★☆☆☆(やや易しい)
図は三相円筒形同期電動機の\( \ \mathrm {V} \ \)曲線である。図中の運転点(\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \),\( \ \mathrm {C} \ \)点)における同期機の諸量に関して,次の問に答えよ。
ただし,端子電圧は\( \ V_{\mathrm {n}} \ \mathrm {[p.u.]} \ \)一定であり,同期機の同期リアクタンスは\( \ X_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)とする。また,鉄心の磁気飽和は無視し,無負荷誘導起電力\( \ E \ \mathrm {[p.u.]} \ \)は界磁電流\( \ I_{\mathrm {f}} \ \mathrm {[p.u.]} \ \)に比例して\( \ E=kI_{\mathrm {f}} \ \)で表されるものとする。巻線抵抗や各種損失は無視する。
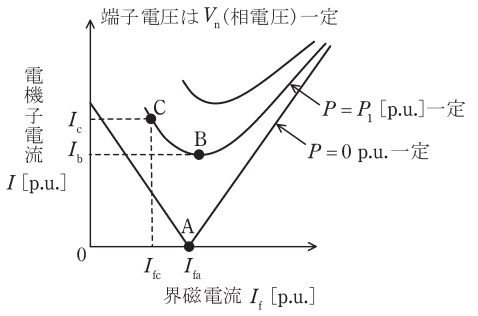
(1) 図中の出力\( \ P=0 \ \mathrm {p.u.} \ \)の\( \ \mathrm {V} \ \)曲線上の運転において,界磁電流\( \ I_{\mathrm {f}} \ \)を変化させると,図中の\( \ \mathrm {A} \ \)点にて電機子電流\( \ I \ \)が\( \ 0 \ \mathrm {p.u.} \ \)となった。このときの界磁電流\( \ I_{\mathrm {fa}} \ \mathrm {[p.u.]} \ \)を\( \ k \ \)と\( \ V_{\mathrm {n}} \ \)を用いて表せ。
(2) 図中の出力\( \ P=P_{1} \ \mathrm {[p.u.]} \ \)の\( \ \mathrm {V} \ \)曲線上の運転において,界磁電流\( \ I_{\mathrm {f}} \ \)を変化させると,図中の\( \ \mathrm {B} \ \)点にて電機子電流\( \ I \ \)の値が最小となった。このときの電機子電流\( \ I_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)を\( \ P_{1} \ \)と\( \ V_{\mathrm {n}} \ \)で表せ。
(3) 図中の出力\( \ P=P_{1} \ \)の\( \ \mathrm {V} \ \)曲線上の運転において,界磁電流を\( \ I_{\mathrm {fc}} \ \mathrm {[p.u.]} \ \)とすると,図中の\( \ \mathrm {C} \ \)点の運転状態となり,このとき電機子電流は\( \ I_{\mathrm {c}} \ \mathrm {[p.u.]} \ \),無負荷誘導起電力は\( \ E_{\mathrm {c}} \ \mathrm {[p.u.]} \ \),力率角は\( \ \theta _{\mathrm {c}} \ \)(遅れ),負荷角(内部相差角)は\( \ \delta _{\mathrm {c}} \ \)であった。\( \ \mathrm {C} \ \)点の運転状態における,\( \ {\dot E}_{\mathrm {c}} \ \),\( \ {\dot V}_{\mathrm {n}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \),\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {c}} \ \),力率角\( \ \theta _{\mathrm {c}} \ \),負荷角\( \ \delta _{\mathrm {c}} \ \)を記入したフェーザ図を描け。ただし,基準フェーザは\( \ {\dot V}_{\mathrm {n}} \ \)とする。
(4) 図中の\( \ \mathrm {C} \ \)点の運転状態における電機子電流\( \ I_{\mathrm {c}} \ \)を,\( \ E_{\mathrm {c}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ V_{\mathrm {n}} \ \),\( \ \cos \delta _{\mathrm {c}} \ \)で表す式を示せ。
(5) 小問(4)で求めた\( \ I_{\mathrm {c}} \ \)を表す式から\( \ \cos \delta _{\mathrm {c}} \ \)と\( \ E_{\mathrm {c}} \ \)を消去して,電機子電流\( \ I_{\mathrm {c}} \ \)を\( \ V_{\mathrm {n}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ P_{1} \ \)及び\( \ kI_{\mathrm {fc}} \ \)で表す式(すなわち\( \ \mathrm {V} \ \)曲線を表す式)を示せ。
【ワンポイント解説】
同期機の\( \ \mathrm {V} \ \)曲線からの出題となります。(1),(2)はフェーザ図を描かなくても解くことができますが,本問のような問題は(1)からベクトル図をきちんと描いて解いた方が間違いが少なくなると思います。
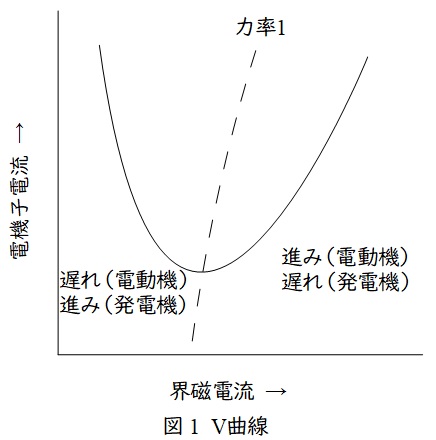
1.同期機の\( \ \mathrm {V} \ \)曲線
同期機の\( \ \mathrm {V} \ \)曲線は図1の通りとなります。図の通り界磁電流を増加させると電機子電流は力率\( \ 1 \ \)を最下点として\( \ \mathrm {V} \ \)字に上昇していくという特性があります。発電機と電動機では遅れと進みが逆になります。
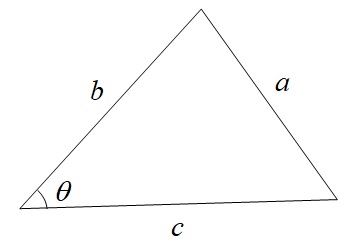
2.余弦定理
下図のような三角形において,
\[
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立します。
【解答】
(1)電機子電流\( \ I \ \)が\( \ 0 \ \mathrm {[p.u.]} \ \)となったときの界磁電流\( \ I_{\mathrm {fa}} \ \mathrm {[p.u.]} \ \)
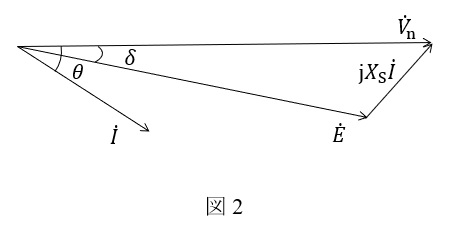
題意に沿ってベクトル図を描くと図2のようになる。
電機子電流\( \ I \ \)が\( \ 0 \ \mathrm {[p.u.]} \ \)なので,\( \ E=V_{\mathrm {n}} \ \)となる。
よって,\( \ E=kI_{\mathrm {f}} \ \)の関係より,
\[
\begin{eqnarray}
I_{\mathrm {fa}}&=&\frac {E}{k} \\[ 5pt ]
&=&\frac {V_{\mathrm {n}}}{k} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)電機子電流\( \ I \ \)が最小となったときの電機子電流\( \ I_{\mathrm {b}} \ \mathrm {[p.u.]} \ \)
図2より,同期機の出力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&V_{\mathrm {n}}I\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
であるので,力率\( \ 1 \ \)である\( \ \mathrm {B} \ \)点での出力\( \ P_{1} \ \)は,
\[
\begin{eqnarray}
P_{1}&=&V_{\mathrm {n}}I_{\mathrm {b}} \\[ 5pt ]
I_{\mathrm {b}}&=&\frac {P_{1}}{V_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)図中の\( \ \mathrm {C} \ \)点の運転状態となったときのフェーザ図
ワンポイント解説「1.同期機の\( \ \mathrm {V} \ \)曲線」の通り,\( \ \mathrm {C} \ \)点における力率は遅れ力率であるから,フェーザ図は図3のようになる。

(4)\( \ \mathrm {C} \ \)点の運転状態における電機子電流\( \ I_{\mathrm {c}} \ \)を,\( \ E_{\mathrm {c}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ V_{\mathrm {n}} \ \),\( \ \cos \delta _{\mathrm {c}} \ \)で表す式
図3に余弦定理を適用すると,
\[
\begin{eqnarray}
\left( X_{\mathrm {S}}I_{\mathrm {c}} \right) ^{2}&=&V_{\mathrm {n}}^{2}+E_{\mathrm {c}}^{2}-2V_{\mathrm {n}}E_{\mathrm {c}}\cos \delta _{\mathrm {c}} \\[ 5pt ]
I_{\mathrm {c}}^{2}&=&\frac {V_{\mathrm {n}}^{2}+E_{\mathrm {c}}^{2}-2V_{\mathrm {n}}E_{\mathrm {c}}\cos \delta _{\mathrm {c}} }{X_{\mathrm {S}}^{2}} \\[ 5pt ]
I_{\mathrm {c}}&=&\frac {\sqrt {V_{\mathrm {n}}^{2}+E_{\mathrm {c}}^{2}-2V_{\mathrm {n}}E_{\mathrm {c}}\cos \delta _{\mathrm {c}} }}{X_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ I_{\mathrm {c}} \ \)を\( \ V_{\mathrm {n}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ P_{1} \ \)及び\( \ kI_{\mathrm {fc}} \ \)で表す式
同期電動機の出力は,
\[
\begin{eqnarray}
P_{1}&=&\frac {E_{\mathrm {c}}V_{\mathrm {n}}}{X_{\mathrm {s}}}\sin \delta _{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
であるので,この式を\( \ \sin \delta \ \)について整理すると,
\[
\begin{eqnarray}
\sin \delta _{\mathrm {c}}&=&\frac {P_{1}X_{\mathrm {s}}}{E_{\mathrm {c}}V_{\mathrm {n}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \cos \delta _{\mathrm {c}}\ \)は,
\[
\begin{eqnarray}
\cos \delta _{\mathrm {c}}&=&\sqrt {1-\sin ^{2}\delta _{\mathrm {c}}} \\[ 5pt ]
&=&\sqrt {1-\left( \frac {P_{1}X_{\mathrm {s}}}{E_{\mathrm {c}}V_{\mathrm {n}}}\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを(4)の解答式に代入して整理すると,
\[
\begin{eqnarray}
I_{\mathrm {c}}&=&\frac {\sqrt {V_{\mathrm {n}}^{2}+E_{\mathrm {c}}^{2}-2V_{\mathrm {n}}E_{\mathrm {c}}\cos \delta _{\mathrm {c}} }}{X_{\mathrm {S}}} \\[ 5pt ]
&=&\frac {\sqrt {\displaystyle V_{\mathrm {n}}^{2}+E_{\mathrm {c}}^{2}-2V_{\mathrm {n}}E_{\mathrm {c}}\sqrt {1-\left( \frac {P_{1}X_{\mathrm {s}}}{E_{\mathrm {c}}V_{\mathrm {n}}}\right) ^{2}}}}{X_{\mathrm {S}}} \\[ 5pt ]
&=&\frac {\sqrt {\displaystyle V_{\mathrm {n}}^{2}+E_{\mathrm {c}}^{2}-2\sqrt {\left( E_{\mathrm {c}}V_{\mathrm {n}}\right) ^{2}-\left( P_{1}X_{\mathrm {s}}\right) ^{2}}}}{X_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より\( \ E_{\mathrm {c}}=kI_{\mathrm {fc}} \ \)であるから,
\[
\begin{eqnarray}
I_{\mathrm {c}}&=&\frac {\sqrt {\displaystyle V_{\mathrm {n}}^{2}+\left( kI_{\mathrm {fc}}\right) ^{2}-2\sqrt {\left( kI_{\mathrm {fc}}V_{\mathrm {n}}\right) ^{2}-\left( P_{1}X_{\mathrm {s}}\right) ^{2}}}}{X_{\mathrm {S}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん