《機械》〈パワーエレクトロニクス〉[R01:問3]自励式無効電力補償装置に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，自励式無効電力補償装置$ \ \mathrm {STATCOM} \ $に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

自励式無効電力補償装置$ \ \mathrm {STATCOM} \ $は，$ \ \fbox {　（１）　} \ $の交流端子を連系リアクトルを介して交流系統に，直流端子を直流コンデンサに接続して構成する。$ \ \fbox {　（１）　} \ $の交流端子電圧の振幅，周波数及び位相を系統電圧と等しくすれば，交流側電流は零となる。この状態から，系統電圧に比べて，交流端子電圧の$ \ \fbox {　（２）　} \ $すると，$ \ \mathrm {STATCOM} \ $は進相コンデンサのように振る舞い，進み無効電力を吸収する。また，系統電圧に比べて，交流端子電圧の$ \ \fbox {　（３）　} \ $すると，$ \ \fbox {　（１）　} \ $に有効電力が流入するので，$ \ \mathrm {STATCOM} \ $ではこれが零となるように制御する。

変換器の$ \ \mathrm {PWM} \ $制御により変調率を調節して無効電力を制御することもできるが，変調率を一定としたままで，直流コンデンサ電圧を調節することでも無効電力を制御できる。$ \ 120 \ $度通電の三相方形波変換器の直流コンデンサ電圧を$ \ V_{\mathrm {d}} \ $とすると，変換器の交流端子の線間電圧の基本波成分実効値は$ \ \displaystyle V_{l}=\frac {\sqrt{6}}{\pi}V_{\mathrm {d}} \ $である。この変換器を$ \ X=0.3 \ \mathrm {p.u.} \ $の連系リアクトルを介して$ \ 6.6 \ \mathrm {kV} \ $の三相正弦波交流系統に接続して定格の進み無効電力を吸収する場合，連系リアクトルでの電圧降下を補償するため，変換器の交流端子の線間電圧基本波成分実効値を$ \ 1.3 \ \mathrm {p.u.} \ $とする必要があるので，直流コンデンサ電圧を$ \ \fbox {　（４）　} \ $にすればよい。このとき，$ \ 5 \ $次高調波に対する連系リアクトルのリアクタンスは，$ \ X_{5}=5X=5\times 0.3=1.5 \ \mathrm {p.u.} \ $であり，変換器の交流端子の線間電圧の$ \ 5 \ $次高調波成分は基本波成分の$ \ \displaystyle \frac {1}{5} \ $であるので，交流側電流の$ \ 5 \ $次高調波成分は基本波成分の$ \ \fbox {　（５）　} \ $程度であり，サイリスタを用いた他励式無効電力補償装置に比べて，高調波発生量は少ない。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　20.0 \ ％　　　　　&（ロ）&　周波数を低く　　　　　&（ハ）&　位相を遅れに \\[ 5pt ] &（ニ）&　振幅を小さく　　　　　&（ホ）&　電流形変換器　　　　　&（ヘ）&　16.7 \ ％ \\[ 5pt ] &（ト）&　17.3 \ ％　　　　　&（チ）&　位相を進みに　　　　　&（リ）&　周波数を高く \\[ 5pt ] &（ヌ）&　9.33 \ \mathrm {kV}　　　　　&（ル）&　交流直接変換器　　　　　&（ヲ）&　8.58 \ \mathrm {kV} \\[ 5pt ] &（ワ）&　振幅を大きく　　　　　&（カ）&　11.0 \ \mathrm {kV}　　　　　&（ヨ）&　電圧形変換器 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {STATCOM} \ $に関する問題で，近年１種や２種においても頻出の分野となっています。自励式$ \ \mathrm {SVC} \ $は系統電圧低下時にも高い補償能力が得られるため，電圧安定性を高める効果が他励式$ \ \mathrm {SVC} \ $と比較して優れるという特徴があります。

1.$ \ \mathrm {STATCOM} \ $
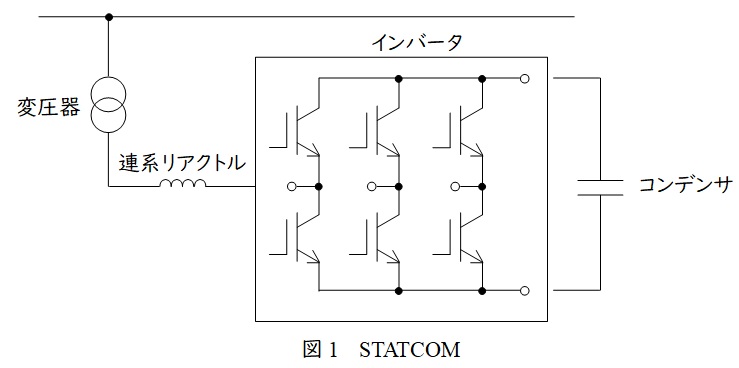
図1のようにインバータを用いることにより，進みから遅れまで無効電力を連続的に制御する方式で，$ \ \mathrm {PWM} \ $制御により低次高調波の抑制を図ることができます。
$ \ \mathrm {STATCOM} \ $は変圧器，連系リアクトル，$ \ \mathrm {IGBT} \ $等の自己消弧形の素子及びコンデンサから構成された電圧形インバータ等から構成されます。

【解答】

(1)解答：ヨ
題意より，解答候補は（ホ）電流形変換器，（ル）交流直接変換器，（ヨ）電圧形変換器，となると思います。$ \ \mathrm {STATCOM} \ $は直流端子に直流コンデンサを接続し，直流側の電圧を$ \ \mathrm {IGBT} \ $等のスイッチング素子により交流側に伝達するので，電圧形変換器となります。

(2)解答：ワ
題意より，解答候補は（ロ）周波数を低く，（ハ）位相を遅れに，（ニ）振幅を小さく，（チ）位相を進みに，（リ）周波数を高く，（ワ）振幅を大きく，となると思います。
系統電圧を$ \ V=一定 $とし，インバータの電圧を$ \ V_{\mathrm {i}} \ $，連系リアクトルのリアクタンスを$ \ X \ $，リアクタンスを流れる電流を$ \ I \ $とすると，
\[
\begin{eqnarray}
V &=&V_{\mathrm {i}}+\mathrm {j}XI \\[ 5pt ] I&=&\frac {V-V_{\mathrm {i}}}{\mathrm {j}X} \\[ 5pt ] &=&-\mathrm {j}\frac {V-V_{\mathrm {i}}}{X} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ V＜V_{\mathrm {i}} \ $となると，$ \ I=\mathrm {j}I_{\mathrm {q}} \ $（ただし，$ \ I_{\mathrm {q}} ＞0 \ $となり，進み電流になります。よって，進み無効電力を吸収することになります。）したがって，振幅を大きくが正答となります。

(3)解答：ハ
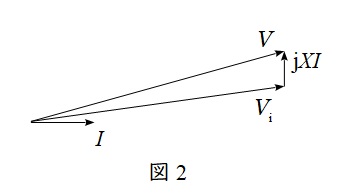
題意より，解答候補は（ロ）周波数を低く，（ハ）位相を遅れに，（ニ）振幅を小さく，（チ）位相を進みに，（リ）周波数を高く，（ワ）振幅を大きく，となると思います。系統から有効電力が流入した時のベクトル図は図2のようになります。このとき，交流端子電圧は系統電圧より遅れ位相となります。

(4)解答：カ
題意より，交流端子電圧の基本波成分の実効値は$ \ 1.3 \ \mathrm {p.u.} \ $であり，$ \ \displaystyle V_{l}=\frac {\sqrt{6}}{\pi}V_{\mathrm {d}} \ $の関係があるので，
\[
\begin{eqnarray}
V_{\mathrm {d}} &=&\frac {\pi}{\sqrt{6}}V_{l} \\[ 5pt ] &=&\frac {\pi}{\sqrt{6}}\times 1.3 \\[ 5pt ] &≒&1.6673 \ \mathrm {[p.u.]} \\[ 5pt ] &≒&11.004　→　11.0 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
題意より，交流端子電圧の第$ \ 5 \ $調波成分の実効値は$ \ \displaystyle \frac {1.3}{5}=0.26 \ \mathrm {p.u.} \ $であり，系統の第$ \ 5 \ $調波成分は零であるとすると，
\[
\begin{eqnarray}
V_{5} &=& V_{\mathrm {l5}}+\mathrm {j}5XI_{\mathrm {5}} \\[ 5pt ] 0 &=& 0.26+\mathrm {j}5\times 0.3I_{\mathrm {5}} \\[ 5pt ] I_{\mathrm {5}}&≒&\mathrm {j}0.17333 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。一方，基本波成分においては，
\[
\begin{eqnarray}
V &=&V_{\mathrm {l}}+\mathrm {j}XI \\[ 5pt ] 1 &=&1.3+\mathrm {j}0.3I \\[ 5pt ] I&=&\mathrm {j}1.0 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となるので，交流側電流の第$ \ 5 \ $次高調波成分は基本波成分に対して，
\[
\begin{eqnarray}
\frac {I_{\mathrm {5}}}{I} &=&\frac {\mathrm {j}0.17333}{\mathrm {j}1.0} \\[ 5pt ] &=&0.17333　→　17.3 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。