【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相誘導電動機の最大トルクに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
一定電圧\( \ V_{1} \ \)(線間電圧),一定周波数の電源に接続した三相誘導電動機の星形結線\( \ 1 \ \)相分の\( \ \mathrm {L} \ \)形等価回路において,一次抵抗\( \ r_{1} \ \),二次抵抗の一次側換算値\( \ r_{2}^{\prime } \ \),一次漏れリアクタンス\( \ x_{1} \ \),二次漏れリアクタンスの一次側換算値\( \ x_{2}^{\prime } \ \)とすると,任意の滑り\( \ s \ \)における一次換算の二次電流\( \ I_{2} \ \)は,
\[
I_{2}=\fbox { (1) } ・・・・・・・・・・・・・①
\]
となる。二次入力\( \ P_{2} \ \)は,
\[
P_{2}=3\frac {r_{2}^{\prime }}{s}{I_{2}}^{2} ・・・・・・・・・・・・・②
\]
で表される。同期角速度を\( \ \omega _{s} \ \)とすれば,任意の滑り\( \ s \ \)における発生トルク\( \ T \ \)は,①式及び②式を用いて,
\[
T=\fbox { (2) } ・・・・・・・・・・・・・③
\]
で表される。③式において,滑りに対するトルク特性でピークとなる最大トルク\( \ T_{\mathrm {m}} \ \)を停動トルクといい,\( \ T_{\mathrm {m}} \ \)を発生するときの滑り\( \ s_{\mathrm {m}} \ \)を求めると,
\[
s_{\mathrm {m}}=\fbox { (3) } ・・・・・・・・・・・・・④
\]
となる。このときの\( \ T_{\mathrm {m}} \ \)は,④式を③式に代入して,
\[
T_{\mathrm {m}}=\fbox { (4) } ・・・・・・・・・・・・・⑤
\]
である。
③式において,\( \ \displaystyle \frac {r_{2}^{\prime }}{s} \ \)が一定である限り\( \ T \ \)は一定となる。これを利用して,上記の\( \ \mathrm {L} \ \)形等価回路定数をもつ巻線形誘導電動機の二次側に抵抗器を挿入し,その抵抗1相分の一次側換算値を\( \ R \ \)とすれば,\( \ r_{2}^{\prime }+R \ \)を変化させることにより同一トルクを発生する\( \ s \ \)を変えることができる。例えば,巻線形誘導電動機で始動時にトルクを最大とするための\( \ r_{2}^{\prime }+R \ \)は,
\[
r_{2}^{\prime }+R=\fbox { (5) }
\]
で与えられる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 2\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} &(ロ)& \frac {V_{1}}{\sqrt {\left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
&(ハ)& \frac {3{V_{1}}^{2}}{2\omega _{s}\left[ r_{1}+\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right] } &(ニ)& \frac {r_{2}^{\prime }}{\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
&(ホ)& \frac {V_{1} / \sqrt {3}}{\sqrt {\left( r_{1}+sr_{2}^{\prime }\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} &(ヘ)& \sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
&(ト)& \frac {3{V_{1}}^{2}}{\omega _{s}\left[ r_{1}+\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right] } &(チ)& \frac {1}{2}\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
&(リ)& \frac {V_{1} / \sqrt {3}}{\sqrt {\left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} &(ヌ)& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}s\left[ \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&(ル)& \frac {r_{2}^{\prime }}{s\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} &(ヲ)& \frac {{V_{1}}^{2}}{2\omega _{s}\left[ r_{1}+\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right] } \\[ 5pt ]
&(ワ)& \frac {sr_{2}^{\prime }}{\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} &(カ)& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}s\left[ \left( r_{1}+sr_{2}^{\prime }\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&(ヨ)& \frac {3r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}s\left[ \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] }
\end{eqnarray}
\]
【ワンポイント解説】
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は一次試験,二次試験共非常によく出題されます。本問の内容もそのまま二次試験に出題されてもおかしくない問題です。確実にマスターし,早く正確に計算できるようにしましょう。
1.電動機の\( \ \mathrm {L} \ \)形等価回路
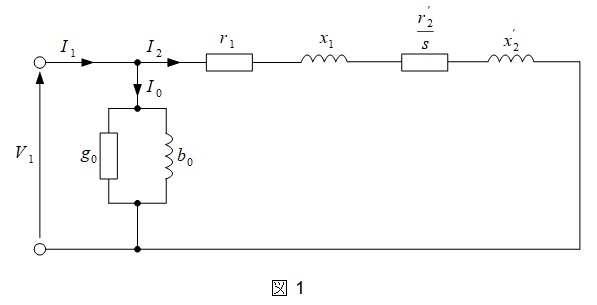
電動機の一相あたりの\( \ \mathrm {L} \ \)形等価回路は図1のようになります。\( \ \mathrm {L} \ \)形等価回路は確実に描けるようにしておきましょう。本問では励磁回路は関係ありません。また,図1での\( \ V_{1} \ \)は相電圧です。問題文との相違に注意して下さい。
\[
\begin{eqnarray}
V_{1}&:&一次電圧(相電圧) \\[ 5pt ]
I_{1}&:&一次電流 \\[ 5pt ]
I_{0}&:&励磁電流 \\[ 5pt ]
I^{\prime}_{2}&:&一次側に換算した二次電流 \\[ 5pt ]
r_{1}&:&一次抵抗 \\[ 5pt ]
x_{1}&:&一次リアクタンス \\[ 5pt ]
r_{2}^{\prime}&:&一次側に換算した二次抵抗 \\[ 5pt ]
x_{2}^{\prime}&:&一次側に換算した二次リアクタンス \\[ 5pt ]
g_{0}&:&励磁コンダクタンス \\[ 5pt ]
b_{0}&:&励磁サセプタンス \\[ 5pt ]
s&:&滑り
\end{eqnarray}
\]
2.掛算,割算の微分の公式
\( \ x \ \)の関数\( \ f (x ) \ \)と\( \ g (x ) \ \)が与えられるとき,
\[
\begin{eqnarray}
\left[ f (x )g (x ) \right] ^{\prime } &=& f^{\prime } (x )g (x ) + f (x )g^{\prime } (x )\\[ 5pt ]
\left[ \frac {f (x )}{g (x )} \right] ^{\prime } &=& \frac {f^{\prime } (x )g (x ) – f (x )g^{\prime } (x )}{g (x ) ^{2}}
\end{eqnarray}
\]
となります。
【解答】
(1)解答:リ
\( \ \mathrm {L} \ \)形等価回路より,一次換算の二次側電流\( \ I_{2} \ \)は,
\[
\begin{eqnarray}
I_{2} &=& \left| \frac {V_{1} / \sqrt {3}}{r_{1}+\frac {r_{2}^{\prime}}{s}+\mathrm {j}x_{1}+\mathrm {j}x_{2}^{\prime}}\right| \\[ 5pt ]
&=& \frac {V_{1} / \sqrt {3}}{\sqrt {\left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}
\end{eqnarray}
\]
と求められる。
(2)解答:ヌ
任意の滑り\( \ s \ \)において,トルク\( \ T \ \)は,
\[
\begin{eqnarray}
T &=& \frac {P}{\omega } \\[ 5pt ]
&=& \frac {P_{2}\left( 1-s\right) }{\omega _{s} \left( 1-s \right) } \\[ 5pt ]
&=& \frac {P_{2}}{\omega _{s} }
\end{eqnarray}
\]
の関係があるから,これに問題の①,②を代入すると,
\[
\begin{eqnarray}
T &=& \frac {P_{2}}{\omega _{s} } \\[ 5pt ]
&=& \frac {3r_{2}^{\prime}}{\omega _{s}s }{I_{2}}^{2} \\[ 5pt ]
&=& \frac {3r_{2}^{\prime}}{\omega _{s}s }{\left( \frac {V_{1} / \sqrt {3}}{\sqrt {\left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}\right) }^{2} \\[ 5pt ]
&=& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}s\left[ \left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] }
\end{eqnarray}
\]
と求められる。
(3)解答:ニ
(2)解答式の分母の分数をなくすため,分母分子に\( \ s \ \)をかけると,
\[
\begin{eqnarray}
T &=& \frac {sr_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}\left[ \left( sr_{1}+r_{2}^{\prime }\right) ^{2}+s ^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&=& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}}\frac {s}{\left( sr_{1}+r_{2}^{\prime }\right) ^{2}+s ^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2} }
\end{eqnarray}
\]
と整理できる。\( \ T_{\mathrm {m}} \ \)を発生するときの滑り\( \ s_{\mathrm {m}} \ \)は,\( \ \displaystyle \frac {\mathrm {d}T}{\mathrm {d}s}=0 \ \)の時の\( \ s \ \)の値であるから,ワンポイント解説「2.掛算,割算の微分の公式」により,上式の両辺を微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}T}{\mathrm {d}s} &=& \frac {\mathrm {d}}{\mathrm {d}s}\left[ \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}}\frac {s}{\left( sr_{1}+r_{2}^{\prime }\right) ^{2}+s ^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2} }\right] \\[ 5pt ]
&=& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}}\frac {\left( sr_{1}+r_{2}^{\prime }\right) ^{2}+s ^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2}-s\cdot \left[ 2r_{1}\left( sr_{1}+r_{2}^{\prime }\right) +2s \left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] }{\left[ \left( sr_{1}+r_{2}^{\prime }\right) ^{2}+s ^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] ^{2} } \\[ 5pt ]
&=& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}}\frac {-s^{2}r_{1}^{2}+{r_{2}^{\prime }}^{2}-s^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2} }{\left[ \left( sr_{1}+r_{2}^{\prime }\right) ^{2}+s ^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] ^{2} }
\end{eqnarray}
\]
となる。ここで,滑り\( \ s_{\mathrm {m}} \ \)は,\( \ \displaystyle \frac {\mathrm {d}T}{\mathrm {d}s}=0 \ \)となる時の滑りであるため,
\[
\begin{eqnarray}
-s_{\mathrm {m}}^{2}r_{1}^{2}+{r_{2}^{\prime }}^{2}-s_{\mathrm {m}}^{2}\left( x_{1}+x_{2}^{\prime }\right) ^{2}&=&0 \\[ 5pt ]
s_{\mathrm {m}}^{2}\left[ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] &=&{r_{2}^{\prime }}^{2} \\[ 5pt ]
s_{\mathrm {m}}^{2} &=&\frac {{r_{2}^{\prime }}^{2}}{ r_{1}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
s_{\mathrm {m}} &=&\frac {r_{2}^{\prime }}{\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}
\end{eqnarray}
\]
と求められる。
(4)解答:ヲ
\( \ T_{\mathrm {m}} \ \)は滑り\( \ s_{\mathrm {m}} \ \)の時のトルクであるから,
\[
\begin{eqnarray}
T_{\mathrm {m}} &=& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}s_{\mathrm {m}}\left[ \left( r_{1}+\frac {r_{2}^{\prime }}{s_{\mathrm {m}}}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&=& \frac {r_{2}^{\prime }{V_{1}}^{2}}{\omega _{s}\frac {r_{2}^{\prime }}{\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}}\left[ \left( r_{1}+\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&=& \frac {\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}{V_{1}}^{2}}{\omega _{s}\left[ \left( r_{1}+\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&=& \frac {\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}{V_{1}}^{2}}{2\omega _{s}\left[ r_{1}\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}+{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}\right] } \\[ 5pt ]
&=& \frac {{V_{1}}^{2}}{2\omega _{s}\left[ r_{1}+\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}\right] }
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
誘導電動機の始動時の滑りは\( \ 1 \ \)であるため,(3)の解答式に\( \ s_{\mathrm {m}}=1 \ \),\( \ r_{2}^{\prime } → r_{2}^{\prime }+R \ \)を代入すると,
\[
\begin{eqnarray}
1 &=&\frac {r_{2}^{\prime }+R}{\sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}} \\[ 5pt ]
r_{2}^{\prime }+R &=& \sqrt {{r_{1}}^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}}
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん