【問題】
【難易度】★★★★☆(やや難しい)
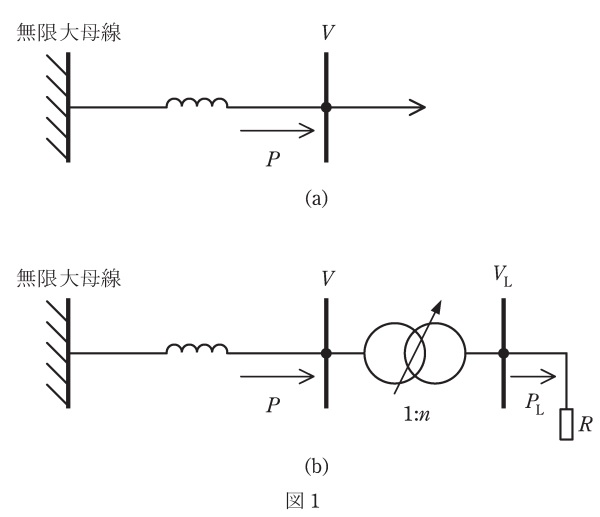
図1に示すように無限大母線からリアクタンスを介して抵抗負荷に電力を供給している場合について考える。ただし,各変数は単位法で表されているものとする。
(1) 図1(a)の系統に対して,受電端母線の電圧の大きさ\( \ V \ \)と受電端有効電力\( \ P \ \)の間の関係(\( \ P-V \ \)カーブ)の概形を図示せよ。図の縦軸・横軸が何を表すかとともに,電圧高め解,電圧低め解の範囲を図中に示せ。
(2) 図1(b)に示すように,電圧\( \ V \ \)の受電端母線に抵抗負荷(抵抗は\( \ R \ \))がタップ切換変圧器(タップ比\( \ 1:n \ \))を介して接続された場合を考える。\( \ V \ \)を負荷消費電力\( \ P_{\mathrm {L}} \ \)と\( \ R \ \),\( \ n \ \)で表す式を求めよ。ただし,変圧器は理想変圧器とする。
(3) 小問(2)の条件のもと,\( \ R \ \)が小さい場合に,さらに\( \ R \ \)が小さくなった場合を考える。このとき,負荷端電圧の大きさ\( \ V_{\mathrm {L}} \ \)を一定に保とうとしてタップ比\( \ n \ \)を増加させると,かえって\( \ V_{\mathrm {L}} \ \)が低下する場合がある(変圧器タップの逆動作現象)。タップ比\( \ n \ \)を増やすと受電端電圧\( \ V \ \)と負荷消費電力\( \ P_{\mathrm {L}} \ \)がどのように変化するかについて,\( \ P-V \ \)カーブに負荷の\( \ P_{\mathrm {L}}-V \ \)特性,又は\( \ P-V_{\mathrm {L}} \ \)カーブに負荷の\( \ P_{\mathrm {L}}-V_{\mathrm {L}} \ \)特性を重ねて図示して\( \ 300 \ \)字程度以内で説明せよ。
【ワンポイント解説】
ノーズカーブを用いた電圧安定性に関する問題です。
ノーズカーブ自体の導出は,少し専門性が強くなるのでなかなか出題されにくいとは思いますが,ノーズカーブの特性自体は2種の平成29年問7でも出題されているので,今後再出題も有り得ると考えておく必要があると思います。
1.受電端母線の電圧の大きさ\( \ V_{\mathrm {r}} \ \)と受電端有効電力\( \ P \ \)の間の関係(\( \ P-V \ \)カーブ)
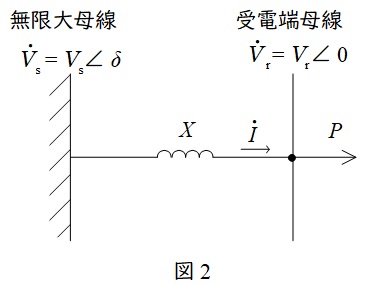
図2のような無限大母線(電圧\( \ {\dot V}_{\mathrm {s}}=V_{\mathrm {s}}∠\delta \ \))からリアクタンス\( \ X \ \)及び受電側母線(電圧\( \ {\dot V}_{\mathrm {r}}=V_{\mathrm {r}}∠0 \ \))を介して抵抗負荷に電力\( \ P \ \)を供給している系統を考えます。
(ここでは,簡単のため抵抗負荷を使用していますが,ノーズカーブの形は抵抗負荷以外でも同じとなります。さらに詳しく知りたい方は専門書を探して見て下さい。)
リアクタンスを流れる電流を\( \ \dot I \ \)とすると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}-{\dot V}_{\mathrm {r}}&=&\mathrm {j}X\dot I \\[ 5pt ]
\dot I&=&\frac {V_{\mathrm {s}}∠\delta -V_{\mathrm {r}}}{\mathrm {j}X} \\[ 5pt ]
\end{eqnarray}
\]
となり,受電端複素電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
&=&V_{\mathrm {r}}\cdot \frac {V_{\mathrm {s}}∠\left( -\delta \right) -V_{\mathrm {r}}}{-\mathrm {j}X} \\[ 5pt ]
&=&\mathrm {j}V_{\mathrm {r}}\cdot \frac {V_{\mathrm {s}}∠\left( -\delta \right) -V_{\mathrm {r}}}{X} \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}∠\left( -\delta +\displaystyle \frac {\pi }{2}\right) -\mathrm {j}V_{\mathrm {r}}^{2}}{X} \\[ 5pt ]
P+\mathrm {j}\frac {V_{\mathrm {r}}^{2}}{X}&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}∠\left( -\delta +\displaystyle \frac {\pi }{2}\right) }{X} \\[ 5pt ]
\end{eqnarray}
\]
となります。両辺の大きさ(絶対値)は等しいので,
\[
\begin{eqnarray}
P^{2}+\left( \frac {V_{\mathrm {r}}^{2}}{X}\right) ^{2}&=&\left( \frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを\( \ V_{\mathrm {r}} \ \)について整理して\( \ V_{\mathrm {r}} \ \)を求めると,
\[
\begin{eqnarray}
\frac {V_{\mathrm {r}}^{4}}{X^{2}}-\frac {V_{\mathrm {s}}^{2}V_{\mathrm {r}}^{2}}{X^{2}}+P^{2}&=&0 \\[ 5pt ]
V_{\mathrm {r}}^{4}-V_{\mathrm {s}}^{2}V_{\mathrm {r}}^{2}+X^{2}P^{2}&=&0 \\[ 5pt ]
V_{\mathrm {r}}^{2}&=&\frac {V_{\mathrm {s}}^{2}±\sqrt {V_{\mathrm {s}}^{4}-4X^{2}P^{2}}}{2} \\[ 5pt ]
V_{\mathrm {r}}&=&\sqrt {\frac {V_{\mathrm {s}}^{2}±\sqrt {V_{\mathrm {s}}^{4}-4X^{2}P^{2}}}{2}} \\[ 5pt ]
\end{eqnarray}
\]
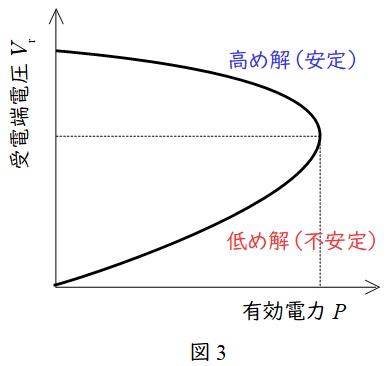
と求められます。上式について,受電端母線の電圧\( \ V_{\mathrm {r}} \ \)と受電端電力\( \ P \ \)の間の関係(\( \ P-V \ \)カーブ)を描くと図3のようになり,これをノーズカーブと呼びます。
図3より,同じ電力において電圧が\( \ 2 \ \)点ある(上式の\( \ 2 \ \)つの解)ことが分かり,電圧が高い方を高め解(安定),電圧が低い方を低め解(不安定)と言います。
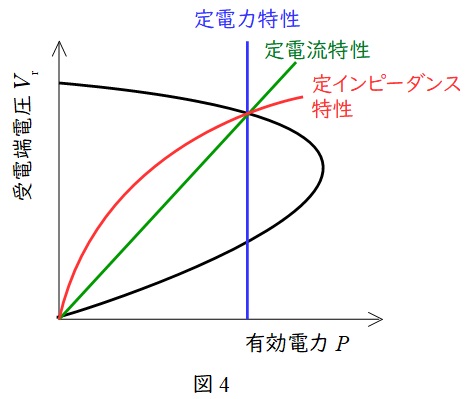
2.\( \ P-V \ \)カーブにおける定電力,定電流,定インピーダンス特性
定電力特性はその名の通り\( \ P \ \)一定の特性なので,図4の青線のような特性となり,定電流特性は\( \ \displaystyle V∝\frac {P}{I} \ \)の関係より図4の緑線のような特性,定インピーダンス特性は,\( \ \displaystyle P∝\frac {V^{2}}{Z} \ \)すなわち\( \ V∝\sqrt {ZP} \ \)の関係があるので,図4の赤線のような特性となります。
3.タップ比\( \ n \ \)を増大させたときの特性の変化
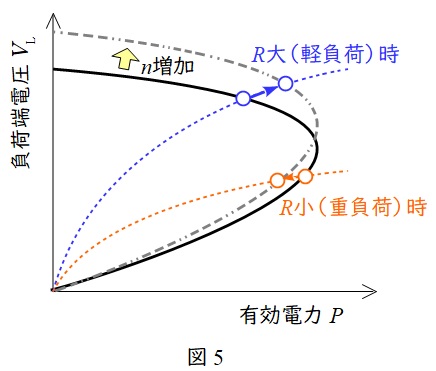
図1(b)の系統において,タップ比\( \ n \ \)を増大させたときの特性変化は図5のようになります。(詳細は電気の神髄をご確認下さい。)
図5より,軽負荷時の電圧高め解においては,\( \ n \ \)を増大させると負荷電力\( \ P_{\mathrm {L}} \ \),負荷端電圧\( \ V_{\mathrm {L}} \ \)ともに増大します。これがタップ切換え時のあってほしい状態となります。
一方,重負荷時の電圧低め解においては,\( \ n \ \)を増大させると負荷電力\( \ P_{\mathrm {L}} \ \),負荷端電圧\( \ V_{\mathrm {L}} \ \)ともに減少し,変圧器タップの本来の目的とは逆の動作が発生します。これを逆動作現象いいます。
【関連する「電気の神髄」記事】
電力系統のP-V曲線と電圧安定性
変圧器タップの逆動作現象(電圧不安定現象)
【解答】
(1)\( \ P-V \ \)カーブ)の概形を図示し,縦軸・横軸,電圧高め解,電圧低め解の範囲を示す
(ポイント)
・ワンポイント解説「1.受電端母線の電圧の大きさ\( \ V_{\mathrm {r}} \ \)と受電端有効電力\( \ P \ \)の間の関係(\( \ P-V \ \)カーブ)」の通りです。
・今回の試験では導出を問われていないので,ノーズカーブを覚えておいて解くようにした方が良いと思います。
(試験センター解答)
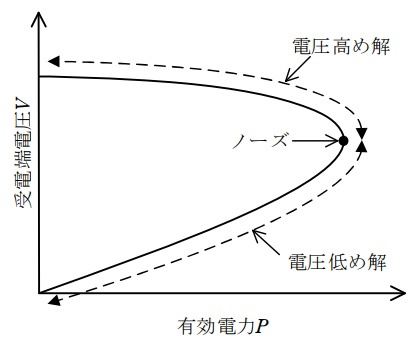
受電端母線の電圧と受電端有効電力の間の関係(\( \ P-V \ \)カーブ)の概形を図に示す。カーブの頂点(ノーズ)より電圧が高い側を電圧高め解,低い側を電圧低め解と呼ぶ。
(2)\( \ V \ \)を負荷消費電力\( \ P_{\mathrm {L}} \ \)と\( \ R \ \),\( \ n \ \)で表す式
図1(b)において,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&\frac {V_{\mathrm {L}}^{2}}{R} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ V_{\mathrm {L}}=nV \ \)であるので,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&\frac {n^{2}V^{2}}{R} \\[ 5pt ]
V^{2}&=&\frac {RP_{\mathrm {L}}}{n^{2}} \\[ 5pt ]
V&=&\frac {\sqrt {RP_{\mathrm {L}}}}{n} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)タップ比\( \ n \ \)を増やすと受電端電圧\( \ V \ \)と負荷消費電力\( \ P_{\mathrm {L}} \ \)がどのように変化するかを説明
(ポイント)
・ワンポイント解説「3.タップ比\( \ n \ \)を増大させたときの特性の変化」の通りです。
・問題文に\( \ 300 \ \)字以内程度となっているので,等価回路を描いて導出する等のいわゆる専門的なメカニズムの説明は不要です。
(試験センター解答)
\( \ P_{\mathrm {L}}-V \ \)特性
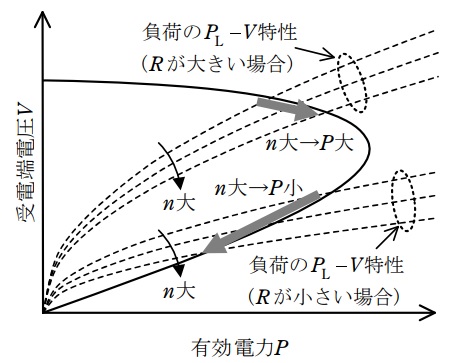
負荷消費電力と受電端電圧は,上述の\( \ P-V \ \)カーブと\( \ P_{\mathrm {L}}-V \ \)特性を表すカーブの交点として定まる。このため,図に示すように,負荷が比較的小さく(\( \ R \ \)が比較的大きく),動作点が電圧高め解にあたる場合には,タップ比\( \ n \ \)を増加すると負荷消費電力は増大する。抵抗負荷であるため,これは負荷端電圧\( \ V_{\mathrm {L}} \ \)が上昇することを表している。
しかし,図中に示すように,負荷が大きい(\( \ R \ \)が小さい)場合に,タップ比\( \ n \ \)が大きくなると,動作点は電圧低め解となることがある。電圧低め解では,タップ比\( \ n \ \)を増大すると受電端電圧とともに負荷消費電力が減少するが,これは負荷端電圧\( \ V_{\mathrm {L}} \ \)が低下することに対応する。これが変圧器タップの逆動作現象である。
\( \ P_{\mathrm {L}}-V_{\mathrm {L}} \ \)特性
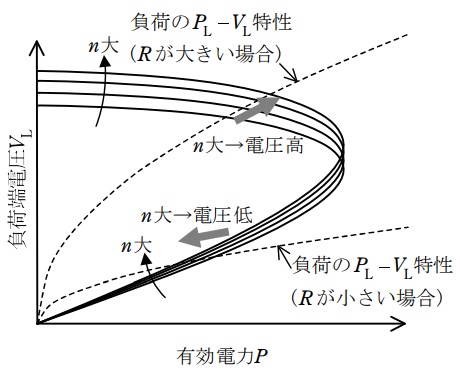
負荷消費電力と負荷端電圧は,\( \ P-V_{\mathrm {L}} \ \)カーブと\( \ P_{\mathrm {L}}-V_{\mathrm {L}} \ \)特性を表すカーブの交点として定まる。ここにタップ比\( \ n \ \)を変化させた場合,図3のように,\( \ P-V_{\mathrm {L}} \ \)カーブは負荷端電圧がタップ比\( \ n \ \)に応じて電圧方向に拡大・縮小した形状を呈する。
負荷が比較的小さい(\( \ R \ \)が比較的大きい)場合には,動作点が電圧高め解にあり,タップ比\( \ n \ \)を増加すると負荷端電圧\( \ V_{\mathrm {L}} \ \)と負荷消費電力\( \ P_{\mathrm {L}} \ \)はともに増大する。
しかし,負荷が大きい(\( \ R \ \)が小さい)場合には,動作点は電圧低め解となることがある。この場合,図中に示すように,タップ比\( \ n \ \)を増大すると,負荷端電圧\( \ V_{\mathrm {L}} \ \)と負荷消費電力\( \ P_{\mathrm {L}} \ \)はともに減少する。これが変圧器タップの逆動作現象である。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん