【問題】
【難易度】★★☆☆☆(やや易しい)
送電線の抵抗とリアクタンスを考慮した送電電力に関して,次の問に答えよ。
ただし,送電端電圧\( \ {\dot V}_{1} \ \)の大きさを\( \ V_{1} \ \),位相を\( \ \delta \ \),受電端電圧\( \ {\dot V}_{2} \ \)の大きさを\( \ V_{2} \ \),位相を零,送電線の抵抗を\( \ r \ \),リアクタンスを\( \ x \ \),送電線電流を\( \ \dot I \ \)とし,電力や電流は送電端から受電端への向きを正,無効電力は遅れを正とする。
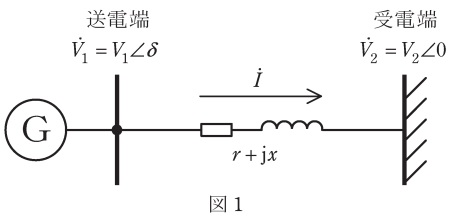
(1) \( \ {\dot V}_{1} \ \)と\( \ {\dot V}_{2} \ \)の関係を答案用紙に印刷されている図2のベクトル図に\( \ {\dot V}_{1} \ \),\( \ r{\dot I} \ \),\( \ \delta \ \)及び\( \ \mathrm {j}x{\dot I} \ \)を追加して示せ。

(2) 送電端から受電端への潮流の送電端側の有効電力を\( \ P \ \),無効電力を\( \ Q \ \)として,\( \ \dot I \ \)を\( \ P \ \),\( \ Q \ \),\( \ {\dot V}_{1} \ \)を用いて表せ。
(3) \( \ r \ \)及び\( \ x \ \)を\( \ V_{1} \ \),\( \ V_{2} \ \),\( \ \delta \ \),\( \ P \ \),\( \ Q \ \)を用いて表せ。なお,\( \ P≠0 \ \)あるいは\( \ Q≠0 \ \)とする。
(4) \( \ r=0.041 \ 4 \ \mathrm {p.u.} \ \),\( \ x=0.245 \ \mathrm {p.u.} \ \)と与えられたとき,\( \ V_{1}=1.08 \ \mathrm {p.u.} \ \),\( \ V_{2}=1.02 \ \mathrm {p.u.} \ \),\( \ P=1.20 \ \mathrm {p.u.} \ \),\( \ Q=0.215 \ \mathrm {p.u.} \ \)となった。この場合の\( \ \sin \delta \ \),\( \ \cos \delta \ \)の値を求めよ。
【ワンポイント解説】
送電線の送電電力に関する問題です。
令和元年度の電験1種と電験2種両方に類題が出題されているので,かなりの受験生が対策をとっていた問題かと思います。
\( \ 1 \ \)種の問題らしく後半の計算がやや多めですが,電力管理科目の中でも最も出題されやすく得点もしやすい内容の一つなので,確実に理解するようにしましょう。
1.オイラーの公式
極座標空間において,
\[
\begin{eqnarray}
\mathrm {e}^{\mathrm {j}\theta }&=&\cos \theta +\mathrm {j}\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
という関係があり,これをオイラーの公式といいます。したがって,\( \ {\dot V}_{\mathrm {s}}= V_{\mathrm {s}}∠\delta \ \),\( \ {\dot V}_{\mathrm {r}}= V_{\mathrm {r}}∠0 \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&V_{\mathrm {s}}\mathrm {e}^{\mathrm {j}\delta } \\[ 5pt ]
&=&V_{\mathrm {s}}\left( \cos \delta +\mathrm {j}\sin \delta \right) \\[ 5pt ]
{\dot V}_{\mathrm {r}}&=&V_{\mathrm {r}}\mathrm {e}^{\mathrm {j}0 } \\[ 5pt ]
&=&V_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.複素電力
送電端電圧を\( \ {\dot V}_{\mathrm {s}} \ \),受電端電圧を\( \ {\dot V}_{\mathrm {r}} \ \),送電線電流を\( \ \dot I \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
【解答】
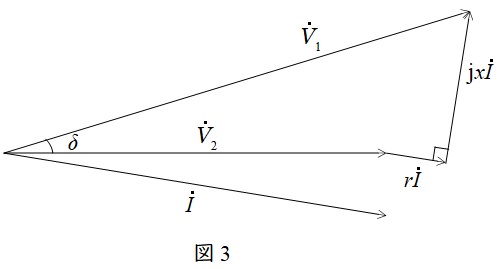
(1)図2のベクトル図に\( \ {\dot V}_{1} \ \),\( \ r{\dot I} \ \),\( \ \delta \ \)及び\( \ \mathrm {j}x{\dot I} \ \)を追加する
抵抗分の電圧降下\( \ r{\dot I} \ \)は\( \ \dot I \ \)と同相,リアクタンス分の電圧降下\( \ \mathrm {j}x{\dot I} \ \)は\( \ \dot I \ \)より\( \ 90° \ \)進みであり,図1より\( \ {\dot V}_{1}={\dot V}_{2}+\left( r+\mathrm {j}x\right) {\dot I} \ \)なので,ベクトル図は図3のようになる。
(2)\( \ \dot I \ \)を\( \ P \ \),\( \ Q \ \),\( \ {\dot V}_{1} \ \)を用いて表す
ワンポイント解説「2.複素電力」の通り,送電端側の送電電力は,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {1}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\overline {\dot I}&=&\frac {P+\mathrm {j}Q}{{\dot V}_{\mathrm {1}}} \\[ 5pt ]
\dot I&=&\frac {\overline {P+\mathrm {j}Q}}{\overline {{\dot V}_{\mathrm {1}}}} \\[ 5pt ]
&=&\frac {P-\mathrm {j}Q}{\overline {{\dot V}_{\mathrm {1}}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ r \ \)及び\( \ x \ \)を\( \ V_{1} \ \),\( \ V_{2} \ \),\( \ \delta \ \),\( \ P \ \),\( \ Q \ \)を用いて表す
図3より,
\[
\begin{eqnarray}
{\dot V}_{1}&=&{\dot V}_{2}+\left( r+\mathrm {j}x\right) {\dot I} \\[ 5pt ]
r+\mathrm {j}x&=&\frac {{\dot V}_{1}-{\dot V}_{2}}{\dot I} \\[ 5pt ]
&=&\frac {{\dot V}_{1}-{\dot V}_{2}}{\displaystyle \frac {P-\mathrm {j}Q}{\overline {{\dot V}_{\mathrm {1}}}}} \\[ 5pt ]
&=&\frac {\left( {\dot V}_{1}-{\dot V}_{2}\right) \overline {{\dot V}_{\mathrm {1}}}}{P-\mathrm {j}Q} ・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「1.オイラーの公式」の通り,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {1}}&=&V_{\mathrm {1}}\left( \cos \delta +\mathrm {j}\sin \delta \right) \\[ 5pt ]
{\dot V}_{\mathrm {2}}&=&V_{\mathrm {2}} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
r+\mathrm {j}x&=&\frac {\left\{ V_{\mathrm {1}}\left( \cos \delta +\mathrm {j}\sin \delta \right) -V_{\mathrm {2}}\right\} V_{\mathrm {1}}\left( \cos \delta -\mathrm {j}\sin \delta \right) }{P-\mathrm {j}Q} \\[ 5pt ]
&=&\frac {V_{\mathrm {1}}^{2} \left( \cos \delta +\mathrm {j}\sin \delta \right) \left( \cos \delta -\mathrm {j}\sin \delta \right) -V_{\mathrm {1}}V_{\mathrm {2}}\left( \cos \delta -\mathrm {j}\sin \delta \right) }{P-\mathrm {j}Q} \\[ 5pt ]
&=&\frac {V_{\mathrm {1}}^{2} \left( \cos ^{2}\delta +\sin ^{2}\delta \right) -V_{\mathrm {1}}V_{\mathrm {2}}\left( \cos \delta -\mathrm {j}\sin \delta \right) }{P-\mathrm {j}Q} \\[ 5pt ]
&=&\frac {V_{\mathrm {1}}^{2} -V_{\mathrm {1}}V_{\mathrm {2}} \cos \delta +\mathrm {j}V_{\mathrm {1}}V_{\mathrm {2}}\sin \delta }{P-\mathrm {j}Q}\cdot \frac {P+\mathrm {j}Q}{P+\mathrm {j}Q} \\[ 5pt ]
&=&\frac {P\left( V_{\mathrm {1}}^{2} -V_{\mathrm {1}}V_{\mathrm {2}} \cos \delta \right) -QV_{\mathrm {1}}V_{\mathrm {2}}\sin \delta +\mathrm {j} \left\{ PV_{\mathrm {1}}V_{\mathrm {2}}\sin \delta +Q\left( V_{\mathrm {1}}^{2} -V_{\mathrm {1}}V_{\mathrm {2}} \cos \delta \right) \right\} }{P^{2}+Q^{2}} \\[ 5pt ]
&=&\frac {PV_{\mathrm {1}}\left( V_{\mathrm {1}} -V_{\mathrm {2}} \cos \delta \right) -QV_{\mathrm {1}}V_{\mathrm {2}}\sin \delta +\mathrm {j} \left\{ PV_{\mathrm {1}}V_{\mathrm {2}}\sin \delta +QV_{\mathrm {1}}\left( V_{\mathrm {1}} -V_{\mathrm {2}} \cos \delta \right) \right\} }{P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,実数部と虚数部を比較すると,
\[
\begin{eqnarray}
r&=&\frac {PV_{\mathrm {1}}\left( V_{\mathrm {1}} -V_{\mathrm {2}} \cos \delta \right) -QV_{\mathrm {1}}V_{\mathrm {2}}\sin \delta }{P^{2}+Q^{2}} \\[ 5pt ]
x&=&\frac {PV_{\mathrm {1}}V_{\mathrm {2}}\sin \delta +QV_{\mathrm {1}}\left( V_{\mathrm {1}} -V_{\mathrm {2}} \cos \delta \right) }{P^{2}+Q^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ \sin \delta \ \),\( \ \cos \delta \ \)の値
①式を変形すると,
\[
\begin{eqnarray}
r+\mathrm {j}x&=&\frac {\left( {\dot V}_{1}-{\dot V}_{2}\right) \overline {{\dot V}_{\mathrm {1}}}}{P-\mathrm {j}Q} \\[ 5pt ]
\left( r+\mathrm {j}x\right) \left( P-\mathrm {j}Q\right) &=&{\dot V}_{1}\overline {{\dot V}_{\mathrm {1}}}-{\dot V}_{2}\overline {{\dot V}_{\mathrm {1}}} \\[ 5pt ]
Pr+Qx+\mathrm {j}\left( Px-Qr\right) &=&V_{1} ^{2}-V_{\mathrm {1}}V_{\mathrm {2}}\left( \cos \delta -\mathrm {j}\sin \delta \right) \\[ 5pt ]
&=&\left(V_{1} ^{2}-V_{\mathrm {1}}V_{\mathrm {2}}\cos \delta \right) +\mathrm {j}V_{\mathrm {1}}V_{\mathrm {2}}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,実数部と虚数部を比較すると,
\[
\begin{eqnarray}
Pr+Qx&=&V_{1} ^{2}-V_{\mathrm {1}}V_{\mathrm {2}}\cos \delta \\[ 5pt ]
\cos \delta &=&\frac {V_{1} ^{2}-\left( Pr+Qx\right) }{V_{\mathrm {1}}V_{\mathrm {2}}} \\[ 5pt ]
Px-Qr&=&V_{\mathrm {1}}V_{\mathrm {2}}\sin \delta \\[ 5pt ]
\sin \delta &=&\frac {Px-Qr}{V_{\mathrm {1}}V_{\mathrm {2}}} \\[ 5pt ]
\end{eqnarray}
\]
と整理できるので,各値を代入すると,
\[
\begin{eqnarray}
\cos \delta &=&\frac {1.08 ^{2}-\left( 1.20\times 0.0414 +0.215\times 0.245\right) }{1.08\times 1.02} \\[ 5pt ]
&≒&0.966 \\[ 5pt ]
\sin \delta &=&\frac {1.20\times 0.245-0.215\times 0.0414}{1.08\times 1.02} \\[ 5pt ]
&≒&0.259 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん