《電力》〈送電〉[R05:問6]電線のたるみの公式の導出に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電線のたるみに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

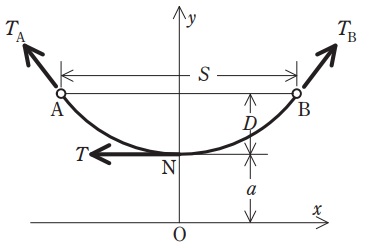
電線のたるみは，電線の材質が一様でたわみ性があるものとみなせば，理論的には\( \ \fbox {　 （１） 　} \ \)曲線となる。電線支持点に高低差のない径間の場合，図において点\( \ \mathrm {O} \ \)を原点とする\( \ \fbox {　 （１） 　} \ \)曲線は次式であらわされる。
\[
\begin{eqnarray}
y &=& \ \fbox {　 （２） 　} \ =a\left( 1+\frac {x^{2}}{2!a^{2}}+\frac {x^{4}}{4!a^{4}}+\frac {x^{6}}{6!a^{6}}+\cdots \right) \\[ 5pt ] \end{eqnarray}
\] 実際の送電線路では，たるみ\( \ D \ \mathrm {[m]} \ \)が径間\( \ S \ \mathrm {[m]} \ \)に比べて十分に小さいため，放物線とみなして\( \ y= \ \fbox {　 （３） 　} \ \)を活用する。

ここに\( \ a \ \)は定数で，曲線の最低点\( \ \mathrm {N} \ \)の\( \ y \ \)座標を示す。\( \ a \ \)は，単位長あたりの電線重量を\( \ W_{\mathrm {c}} \ \mathrm {[kg / m]} \ \)，電線の水平張力\( \ T \ \mathrm {[kg]} \ \)を用いて\( \ \fbox {　 （４） 　} \ \)と表せる。

原点を\( \ \mathrm {O} \ \)から点\( \ \mathrm {N} \ \)に移せば，\( \ y= \ \fbox {　 （５） 　} \ \)となり，\( \ \displaystyle x=\frac {S}{2} \ \)，\( \ a=\fbox {　 （４） 　} \ \)を代入すると，たるみ\( \ D=\fbox {　 （６） 　} \ \)となる。

図において，電線の支持点\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)における張力\( \ T_{\mathrm {A}} \ \)，\( \ T_{\mathrm {B}} \ \)は，最低点における水平張力\( \ T \ \)と\( \ W_{\mathrm {c}} \ \)と\( \ D \ \)を用いて，\( \ T_{\mathrm {A}}=T_{\mathrm {B}}= \ \fbox {　 （７） 　} \ \)であり，電線の各点の張力を全て水平張力と同一として設計しても大差はない。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　T\times W_{\mathrm {c}}D　　　　　&（ロ）&　T+ W_{\mathrm {c}}D　　　　　&（ハ）&　\frac {T}{W_{\mathrm {c}}} \\[ 5pt ] &（ニ）&　\frac {W_{\mathrm {c}}}{T}　　　　　&（ホ）&　\frac {x}{a}　　　　　&（ヘ）&　a\cos \frac {x}{a} \\[ 5pt ] &（ト）&　a+\frac {x}{a}　　　　　&（チ）&　a\cosh \frac {x}{a}　　　　　&（リ）&　\frac {x^{2}}{2a} \\[ 5pt ] &（ヌ）&　a+\frac {x^{2}}{4a}　　　　　&（ル）&　\frac {W_{\mathrm {c}}S}{8T}　　　　　&（ヲ）&　a\sinh \frac {x}{a} \\[ 5pt ] &（ワ）&　カテナリ　　　　　&（カ）&　\frac {8T}{W_{\mathrm {c}}S^{2}}　　　　　&（ヨ）&　\frac {x^{2}}{4a} \\[ 5pt ] &（タ）&　\frac {W_{\mathrm {c}}S^{2}}{8T}　　　　　&（レ）&　T+8W_{\mathrm {c}}D　　　　　&（ソ）&　正弦波 \\[ 5pt ] &（ツ）&　a+\frac {x^{2}}{2a}　　　　　&（ネ）&　2 \ 次　　　　　&& \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電線のたるみの式の導出に関する問題です。
カテナリ曲線を数学で学習されていた方は問題なく解けるかと思いますが，そうでない方は(6)の式を暗記しておき，それ以外の選択肢は(6)の式が成立するようにして導出していくと知識がなくても解けるかと思います。電験では本問のように他の空欄がヒントとなっている場合もありますので，諦めずに解くようにして下さい。

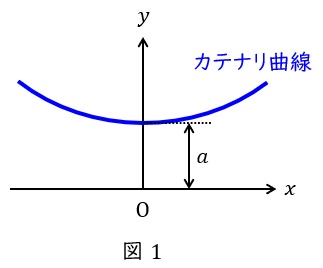
1.カテナリ曲線
一般に図1のように，紐の両端を持って垂らしたときにできる曲線をカテナリ曲線と呼び，
\[
\begin{eqnarray}
y &=& a\cosh \frac {x}{a}=\frac {a\left( \mathrm {e}^{\frac {x}{a}}+\mathrm {e}^{-\frac {x}{a}}\right) }{2} \\[ 5pt ] \end{eqnarray}
\] となります。ただし，単位長さあたりの質量を\( \ \rho \ \mathrm {[kg / m]} \ \)，重力加速度を\( \ g \ \mathrm {[m / s^{2}]} \ \)，\( \ x=0 \ \)での張力を\( \ T_{0} \ \mathrm {[N]} \ \)とすると，\( \ \displaystyle a=\frac {T_{0}}{\rho g} \ \)となります。（カテナリ曲線の導出は微分方程式を用いて導出することができますが，電験対策としては不要です。）これをマクローリン展開\( \ \displaystyle \mathrm {e}^{x}=1+x+\frac {x^{2}}{2!}+\frac {x^{3}}{3!}+\cdots \ \)を用いて展開すると，
\[
\begin{eqnarray}
y &=& \frac {a}{2}\left[ \left\{ 1+\frac {x}{a}+\frac {\displaystyle \left( \frac {x}{a}\right)^{2}}{2!}+\frac {\displaystyle \left( \frac {x}{a}\right)^{3}}{3!}+\cdots \right\} + \left\{ 1-\frac {x}{a}+\frac {\displaystyle \left( \frac {x}{a}\right)^{2}}{2!}-\frac {\displaystyle \left( \frac {x}{a}\right)^{3}}{3!}+\cdots \right\} \right] \\[ 5pt ] &=& a\left\{ 1+\frac {\displaystyle \left( \frac {x}{a}\right)^{2}}{2!}+\frac {\displaystyle \left( \frac {x}{a}\right)^{4}}{4!}+\frac {\displaystyle \left( \frac {x}{a}\right)^{6}}{6!}+\cdots \right\} \\[ 5pt ] &=&a\left( 1+\frac {x^{2}}{2!a^{2}}+\frac {x^{4}}{4!a^{4}}+\frac {x^{6}}{6!a^{6}}+\cdots \right) \\[ 5pt ] &≃&a\left( 1+\frac {x^{2}}{2a^{2}}\right) \\[ 5pt ] &=&a+\frac {x^{2}}{2a} \\[ 5pt ] \end{eqnarray}
\] と二次曲線に近似することができます。

【解答】

(1)解答：ワ
題意より解答候補は，（ワ）カテナリ，（ソ）正弦波，（ネ）\( \ 2 \ \)次，になると思います。
ワンポイント解説「1.カテナリ曲線」の通り，電線のたるみはカテナリ曲線となります。

(2)解答：チ
カテナリ曲線は，ワンポイント解説「1.カテナリ曲線」の通り，
\[
\begin{eqnarray}
y &=& a\cosh \frac {x}{a} \\[ 5pt ] \end{eqnarray}
\] で表される。

(3)解答：ツ
\[
\begin{eqnarray}
y &=& a\cosh \frac {x}{a}=a\left( 1+\frac {x^{2}}{2!a^{2}}+\frac {x^{4}}{4!a^{4}}+\frac {x^{6}}{6!a^{6}}+\cdots \right) \\[ 5pt ] \end{eqnarray}
\] の第\( \ 3 \ \)項以降は十分に小さいとして無視すると，
\[
\begin{eqnarray}
y &=& a\left( 1+\frac {x^{2}}{2!a^{2}} \right) \\[ 5pt ] &=& a\left( 1+\frac {x^{2}}{2a^{2}} \right) \\[ 5pt ] &=& a+\frac {x^{2}}{2a} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ハ
ワンポイント解説「1.カテナリ曲線」の通り，\( \ \displaystyle a=\frac {T}{W_{\mathrm {c}}} \ \)となる。

(5)解答：リ
(3)解答式より，原点を\( \ \mathrm {O} \ \)から点\( \ \mathrm {N} \ \)に移せば，
\[
\begin{eqnarray}
y &=& \frac {x^{2}}{2a} \\[ 5pt ] \end{eqnarray}
\] となる。

(6)解答：タ
(5)解答式に\( \ \displaystyle x=\frac {S}{2} \ \)，\( \ \displaystyle y=D \ \)及び\( \ \displaystyle a=\frac {T}{W_{\mathrm {c}}} \ \)を代入すれば，
\[
\begin{eqnarray}
D &=& \frac {\displaystyle \left( \frac {S}{2}\right) ^{2}}{\displaystyle 2\cdot \frac {T}{W_{\mathrm {c}}}} \\[ 5pt ] &=& \frac {W_{\mathrm {c}}S ^{2}}{8T} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(7)解答：ロ
\( \ \displaystyle a=\frac {T}{W_{\mathrm {c}}} \ \)の関係より，
\[
\begin{eqnarray}
a+D &=& \frac {T_{\mathrm {A}}}{W_{\mathrm {c}}} \\[ 5pt ] T_{\mathrm {A}}&=& W_{\mathrm {c}}\left( a+D\right) \\[ 5pt ] &=& W_{\mathrm {c}}a+W_{\mathrm {c}}D \\[ 5pt ] &=& T+W_{\mathrm {c}}D \\[ 5pt ] \end{eqnarray}
\] と求められる。