【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,対称座標法に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
電力系統の故障電流は,故障点に\( \ \fbox { (1) } \ \)を適用し,電力系統側を電圧源とインピーダンスからなる等価回路で表現して計算するのが一般的である。その際には,故障点に仮想的に設けた端子での三相電圧・電流を対称座標変換し,故障点から見た電力系統を発電機の基本式を用いて表すことにより故障電流を計算することが多い。
対称座標法では,三相(\( \ \mathrm {a} \ \),\( \ \mathrm {b} \ \),\( \ \mathrm {c} \ \)で表す)の電圧・電流を零相,正相,逆相(それぞれ\( \ 0 \ \),\( \ 1 \ \),\( \ 2 \ \)で表す)の電圧・電流に変換する。例えば正相電流\( \ {\dot I}_{1} \ \)は,三相電流を\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)とすれば,\( \ \displaystyle a=-\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \ \)を用いて\( \ \fbox { (2) } \ \)となる。
故障前における故障点の\( \ \mathrm {a} \ \)相電圧を\( \ {\dot E}_{\mathrm {a}} \ \),故障点から見た零相,正相,逆相インピーダンスをそれぞれ\( \ {\dot Z}_{\mathrm {0}} \ \),\( \ {\dot Z}_{\mathrm {1}} \ \),\( \ {\dot Z}_{\mathrm {2}} \ \)とするとき,\( \ 1 \ \)線地絡時(故障相は\( \ \mathrm {a} \ \)相)及び\( \ 3 \ \)線地絡時の故障点電流は次のとおりとなる。ただし,故障点抵抗は\( \ 0 \ \)とする。
・\( \ 1 \ \)線地絡時:\( \ \fbox { (3) } \ \)
・\( \ 3 \ \)線地絡時:\( \ \fbox { (4) } \ \)
上記の計算のためには発電機等の対称分インピーダンスが必要である。発電機,送電線,変圧器の直列インピーダンスは以下の特徴を有する。
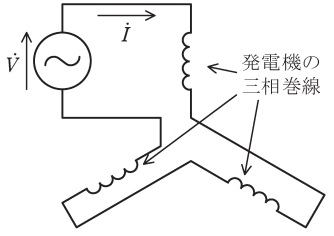
① 発電機:正相の電機子電流は発電機内に機械的な回転方向と同じ方向に回転する回転磁界を,逆相の電機子電流はそれと反対方向に回転する回転磁界を作るのに対して,零相の電機子電流は発電機内に回転磁界を作らない。これらにより,発電機の零相,正相,逆相インピーダンスは異なる値をとる。図は,単相の外部電源(電圧\( \ \dot V \ \))に発電機の三相巻線を直列に接続することにより,発電機の零相インピーダンスを測定する回路である。この場合,\( \ \dot V \ \)は三相電圧の和となるため零相電圧の\( \ \fbox { (5) } \ \)となり,電流\( \ \dot I \ \)は三相電流が等しいため零相電流だけとなる。このため,\( \ \dot V \ \)と\( \ \dot I \ \)より零相インピーダンスが求められる。
② 送電線:正相及び逆相電流が作る電線周辺の磁界の大きさはどちらでも同じとなるため,正相及び逆相インピーダンスは同一となる。また,零相インピーダンスは,零相電流が大地を帰路として各相導体に同位相で流れるため,正相,逆相インピーダンス\( \ \fbox { (6) } \ \)。
③ 変圧器:正相,逆相インピーダンスとしては変圧器の漏れリアクタンスを考慮する必要がある。また零相インピーダンスには,変圧器の結線方式とともにその\( \ \fbox { (7) } \ \)が大きく影響する。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 3 \ 倍 &(ロ)& \frac {{\dot I}_{\mathrm {a}}+a^{2}{\dot I}_{\mathrm {b}}+a{\dot I}_{\mathrm {c}}}{3} \\[ 5pt ]
&(ハ)& {\dot I}_{\mathrm {a}}+a^{2}{\dot I}_{\mathrm {b}}+a{\dot I}_{\mathrm {c}} &(ニ)& \frac {1}{3} \ 倍 \\[ 5pt ]
&(ホ)& より大きい &(ヘ)& ノートンの定理 \\[ 5pt ]
&(ト)& \frac {3{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {1}}} &(チ)& より小さい \\[ 5pt ]
&(リ)& テブナンの定理 &(ヌ)& \frac {3{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
&(ル)& \frac {{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}} &(ヲ)& \frac {\sqrt {3}{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
&(ワ)& 励磁アドミタンス &(カ)& \frac {{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
&(ヨ)& 1 \ 倍 &(タ)& \frac {{\dot I}_{\mathrm {a}}+a{\dot I}_{\mathrm {b}}+a^{2}{\dot I}_{\mathrm {c}}}{3} \\[ 5pt ]
&(レ)& と同一になる &(ソ)& \frac {{\dot E}_{\mathrm {a}}}{{\dot Z}_{\mathrm {1}}} \\[ 5pt ]
&(ツ)& テレヘンの定理 &(ネ)& 中性点接地インピーダンス \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
対称座標法に関する問題です。
基本的に対称座標法は二次試験で計算問題が出題されることが多かったですが,令和3年は一次試験で出題されました。
一次試験としてはやや難しい内容ですが,対称座標法の計算は慣れの部分が大きいため,(3),(4)の導出は覚えるのではなくできるようにしておきましょう。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。上記より,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
1+a+a^{2}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
2.対称座標法
故障計算をする際に非常に便利な方法で,以下のように定義し対称座標変換されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:リ
題意より解答候補は,(ヘ)ノートンの定理,(リ)テブナンの定理,(ツ)テレヘンの定理,になると思います。
対称座標法は故障点にテブナンの定理を適用し,開放電圧と故障点から見たインピーダンスからなる等価回路で表現して計算したものが一般的となります。
(2)解答:タ
ワンポイント解説「2.対称座標法」の通り,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}
\end{eqnarray}
\]
であるため,\( \ {\dot I}_{\mathrm {a}}+a{\dot I}_{\mathrm {b}}+a^{2}{\dot I}_{\mathrm {c}} \ \)を計算し,\( \ {\dot I}_{1} \ \)について整理すると,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}+a{\dot I}_{\mathrm {b}}+a^{2}{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2}+a\left( {\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}\right) +a^{2}\left( {\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}\right) \\[ 5pt ]
&=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2}+a{\dot I}_{0}+ {\dot I}_{1} + a^{2}{\dot I}_{2} +a^{2}{\dot I}_{0}+ {\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
&=&\left( 1+a+a^{2}\right) {\dot I}_{0}+ 3{\dot I}_{1} + \left( 1+a+a^{2}\right) {\dot I}_{2} \\[ 5pt ]
&=&3{\dot I}_{1} \\[ 5pt ]
{\dot I}_{1}&=&\frac {{\dot I}_{\mathrm {a}}+a{\dot I}_{\mathrm {b}}+a^{2}{\dot I}_{\mathrm {c}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヌ
\( \ \mathrm {a} \ \)相に\( \ 1 \ \)線地絡事故が発生すると,ワンポイント解説「2.対称座標法」で定義する電圧・電流において,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2}=0 &・・・・・・ ①& \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}=0 &・・・・・・ ②& \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}=0 &・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
が成立する。②,③より,
\[
\begin{eqnarray}
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
a^{2}{\dot I}_{1} + a{\dot I}_{2} &=& a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\left( a^{2}-a \right) {\dot I}_{1}&=&\left( a^{2}-a \right) {\dot I}_{2} \\[ 5pt ]
{\dot I}_{1}&=& {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}&=&0 \\[ 5pt ]
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{1}&=&0 \\[ 5pt ]
{\dot I}_{0}+ \left( a^{2}+a \right) {\dot I}_{1}&=&0 \\[ 5pt ]
{\dot I}_{0}- {\dot I}_{1}&=&0 \\[ 5pt ]
{\dot I}_{0} &=&{\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
&=&3{\dot I}_{0} \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,対称座標法の関係式を満たす回路は図1のようになり,図1より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}} &=&\left( {\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}\right) \frac {{\dot I}_{\mathrm {a}}}{3} \\[ 5pt ]
{\dot I}_{\mathrm {a}} &=&\frac {3{\dot E}_{\mathrm {a}}}{ {\dot Z}_{\mathrm {0}}+{\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(4)解答:ソ
\( \ 3 \ \)線地絡事故が発生すると,ワンポイント解説「2.対称座標法」で定義する電圧・電流において,
\[
\begin{eqnarray}
&&{\dot V}_{\mathrm {a}} ={\dot V}_{\mathrm {b}}={\dot V}_{\mathrm {c}}=0 &・・・・・・ ④& \\[ 5pt ]
&&{\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} =0 &・・・・・・ ⑤& \\[ 5pt ]
\end{eqnarray}
\]
が成立しなければならないので,⑤より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} &=&0 \\[ 5pt ]
{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} +{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}+{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}&=&0 \\[ 5pt ]
3{\dot I}_{0}+ \left( 1+a+a^{2}\right) {\dot I}_{1} +\left( 1+a+a^{2}\right) {\dot I}_{2} &=&0 \\[ 5pt ]
{\dot I}_{0} &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。これと発電機の基本式から,
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となるので,④式は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} ={\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2}&=&0 \\[ 5pt ]
{\dot V}_{1} + {\dot V}_{2}&=&0 \\[ 5pt ]
{\dot V}_{1} &=& -{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} ={\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2}&=&0 \\[ 5pt ]
a^{2}{\dot V}_{1} – a{\dot V}_{1}&=&0 \\[ 5pt ]
\left( a^{2}-a\right) {\dot V}_{1} &=&0 \\[ 5pt ]
{\dot V}_{1} &=&0 \\[ 5pt ]
{\dot V}_{2} &=&-{\dot V}_{1}=0 \\[ 5pt ]
\end{eqnarray}
\]
となり,発電機の基本式から,
\[
\begin{eqnarray}
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
0&=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot I}_{1}&=&\frac {{\dot E}_{\mathrm {a}}}{Z_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:イ
題意より,\( \ \dot V \ \)は三相電圧の和となるため,ワンポイント解説「2.対称座標法」より,
\[
\begin{eqnarray}
\dot V&=&{\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}} \\[ 5pt ]
&=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2}+{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2}+{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
&=&3{\dot V}_{0}+ \left( 1+a+a^{2}\right) {\dot V}_{1} + \left( 1+a+a^{2}\right) {\dot V}_{2} \\[ 5pt ]
&=&3{\dot V}_{0} \\[ 5pt ]
\end{eqnarray}
\]
となり,零相電圧の\( \ 3 \ \)倍となる。
(6)解答:ホ
題意より解答候補は,(ホ)より大きい,(チ)より小さい,(レ)と同一になる,になると思います。
平衡した三相線路での各線路のインピーダンスを\( \ {\dot Z}_{\mathrm {a}}={\dot Z}_{\mathrm {b}}={\dot Z}_{\mathrm {c}}={\dot Z}_{\mathrm {l}} \ \),各相の相互インダクタンスによる各線路のインピーダンスを\( \ {\dot Z}_{\mathrm {m}} \ \)とすると,零相,正相,逆相の電圧降下\( \ \Delta {\dot V}_{\mathrm {0}} \ \),\( \ \Delta {\dot V}_{\mathrm {1}} \ \),\( \ \Delta {\dot V}_{\mathrm {2}} \ \)は,
\[
\begin{eqnarray}
\Delta {\dot V}_{\mathrm {0}} &=&\left( {\dot Z}_{\mathrm {l}}+2{\dot Z}_{\mathrm {m}}\right) {\dot I}_{\mathrm {0}} \\[ 5pt ]
\Delta {\dot V}_{\mathrm {1}} &=&\left( {\dot Z}_{\mathrm {l}}-{\dot Z}_{\mathrm {m}}\right) {\dot I}_{\mathrm {1}} \\[ 5pt ]
\Delta {\dot V}_{\mathrm {2}} &=&\left( {\dot Z}_{\mathrm {l}}-{\dot Z}_{\mathrm {m}}\right) {\dot I}_{\mathrm {2}} \\[ 5pt ]
\end{eqnarray}
\]
で表され,零相インピーダンスは正相,逆相インピーダンスより大きくなります。
(専門書には導出過程等の記載もありますので,ご興味のある方は調べてみて下さい。)
(7)解答:ネ
題意より解答候補は,(ワ)励磁アドミタンス,(ネ)中性点接地インピーダンス,になると思います。
変圧器の零相インピーダンスは,変圧器の結線方式とともに中性点接地インピーダンスが大きく影響します。
(こちらも専門書には結線方式毎の導出過程等の記載もありますので,ご興味のある方は調べてみて下さい。)






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん