【問題】
【難易度】★★★☆☆(普通)
次の文章は,誘導発電機に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句を解答群の中から選び,その記号をマークシートに記入しなさい。
三相誘導電動機の固定子を電源に接続して,固定子が作る回転磁界の回転方向と同一方向に,他の原動機を用いて\( \ \fbox { (1) } \ \)で回転させると,滑りは負の値となる。このとき,回転子巻線は電動機の場合と逆方向に回転磁束を切り,二次巻線の誘導起電力及び二次電流の方向は,電動機の場合と逆になる。したがって,二次電流と回転磁束とによる\( \ \fbox { (2) } \ \)の方向は,回転子の回転方向と逆になる。固定子電流の方向も電動機の場合と逆になるから,原動機から回転子への機械的入力は,電気的出力となって固定子から電源に送り出されることになる。すなわち,誘導発電機としての動作となる。
このタイプの誘導発電機は以下のような特徴がある。 回転磁束を作るための\( \ \fbox { (3) } \ \)は,誘導発電機が接続されている電源から供給を受けなければならない。周波数は,\( \ \fbox { (4) } \ \)の周波数で定まる。誘導発電機の出力を増加するには,原動機の回転速度を増さなければならない。同期発電機と異なり,始動が簡単で,\( \ \fbox { (5) } \ \)の必要がない。線路に三相短絡を生じた場合,励磁が失われるので,短絡電流は同期機に比べて小さく,持続時間も短い。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& 平滑化 &(ロ)& トルク &(ハ)& 同期速度以下の速度 \\[ 5pt ]
&(ニ)& 有効電力 &(ホ)& 同期速度 &(ヘ)& 励磁電流 \\[ 5pt ]
&(ト)& 無効電力 &(チ)& 乱 調 &(リ)& 電 源 \\[ 5pt ]
&(ヌ)& 二次電流 &(ル)& 電機子電流 &(ヲ)& 同期速度を超える速度 \\[ 5pt ]
&(ワ)& 回転子 &(カ)& 二次入力 &(ヨ)& 同期化 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
誘導発電機の特性や特徴に関する問題です。
誘導発電機を考える上で最大のポイントとなるのはトルクと滑りの関係です。
できるだけ丸暗記に頼るのではなく,等価回路からトルクと滑りの関係を理解していくようにして下さい。
1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \),電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は,
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ]
&=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ]
&=&\frac {4\pi f}{p} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min} ^{-1}]} \ \),回転速度が\( \ N \ \mathrm {[{min} ^{-1}]} \ \)である時,誘導機の滑り\( \ s \ \)は,
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ]
\end{eqnarray}
\]
と定義されるので,\( \ N \ \)について整理すると,
\[
\begin{eqnarray}
s N_{\mathrm {s}}&=&N_{\mathrm {s}}-N \\[ 5pt ]
N&=&\left( 1-s\right) N_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
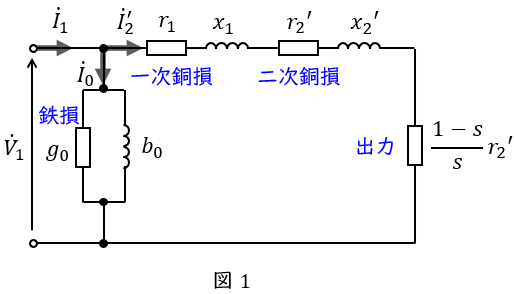
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において,\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧(相電圧),\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流,\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算,\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流,\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗,\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算,\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス,\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算,\( \ s \ \)は滑りとなります。
図1より,出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \),二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ]
P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \),出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \),二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には,
\[
\begin{eqnarray}
P_{2}:P_{\mathrm {o}}:P_{\mathrm {c2}} &=& 1:(1-s):s \\[ 5pt ]
\end{eqnarray}
\]
の関係があることが分かります。
4.滑りの違いによる誘導機の動作の違い
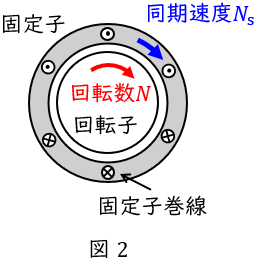
①\( \ s<0 \ \)のとき
\( \ N>N_{\mathrm {s}} \ \)となるので,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min} ^{-1}]} \ \)よりも回転速度\( \ N \ \mathrm {[{min} ^{-1}]} \ \)が高い状態で,どちらも同方向に回転している状態です。このとき,誘導機は誘導発電機として働き,回生制動となり電源側に電力が返還されます。
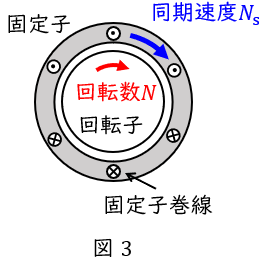
②\( \ 0<s<1 \ \)のとき
\( \ N<N_{\mathrm {s}} \ \)となるので,同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min} ^{-1}]} \ \)よりも回転速度\( \ N \ \mathrm {[{min} ^{-1}]} \ \)が低い状態で,どちらも同方向に回転している状態です。このとき,誘導機は誘導電動機として働き,電源から電力が供給されます。
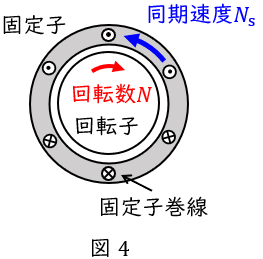
③\( \ s>1 \ \)のとき
回転速度\( \ N \ \mathrm {[{min} ^{-1}]} \ \)に対し同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min} ^{-1}]} \ \)が逆向きに回転している状態で,このとき逆向きに大きなトルクがかかります。このとき,誘導機は誘導ブレーキとして働き,入力は熱として消費されます。回生制動より大きなトルクがかかるので,急ブレーキとして使用します。
5.誘導機のトルクと滑りの関係
等価回路より,三相誘導電動機のトルク\( \ T \ \mathrm {[N\cdot m]} \ \)は,
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ]
&=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ]
&=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
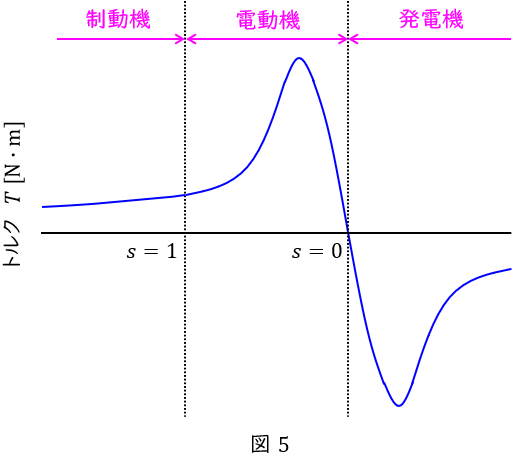
で求められ,この関係式から,トルク\( \ T \ \mathrm {[N\cdot m]} \ \)と滑り\( \ s \ \)の関係を表すと図5のようになります。
6.誘導発電機の同期発電機と比較した特徴
誘導発電機は同期発電機と比較すると以下の特徴があります。
・構造が簡単であるため,丈夫で安価となる
・同期投入の必要がなく,起動時や運転時の操作が簡単
・線路に短絡が生じた場合,励磁がなくなるので,短絡電流の減衰が速く,持続時間も短い
・負荷電流と励磁電流の巻線が同じであるため,回転磁束を得るための励磁電流を電力系統から受けなければならない
・無効電力の調整機能がないため,力率や電圧の調整ができず,単独運転をすることができない
【解答】
(1)解答:ヲ
題意より解答候補は,(ハ)同期速度以下の速度,(ホ)同期速度,(ヲ)同期速度を超える速度,になると思います。
ワンポイント解説「4.滑りの違いによる誘導機の動作の違い」の通り,誘導機の回転子を同期速度を超える速度で運転することにより,滑りは負の値となり発電機として動作します。
(2)解答:ロ
題意より解答候補は,(ロ)トルク,(ニ)有効電力,(ヘ)励磁電流,(ト)無効電力,(ヌ)二次電流,(ル)電機子電流,(カ)二次入力,等になると思います。
ワンポイント解説「5.誘導機のトルクと滑りの関係」の通り,誘導発電機のトルクは負となり,回転子の回転方向と逆となります。図2においてどちらの方向にトルクが加わるかを考えるとイメージしやすいかと思います。
(3)解答:ヘ
題意より解答候補は,(ロ)トルク,(ニ)有効電力,(ヘ)励磁電流,(ト)無効電力,(ヌ)二次電流,(ル)電機子電流,(カ)二次入力,等になると思います。
ワンポイント解説「6.誘導発電機の同期発電機と比較した特徴」の通り,誘導発電機は回転磁束を作るための励磁電流を誘導発電機が接続されている電源から供給しなければなりません。
(4)解答:リ
題意より解答候補は,(ニ)有効電力,(リ)電源,(ワ)回転子,等になると思います。
誘導発電機の周波数は電源の周波数で定まります。おそらく滑り周波数のことを指していると思いますが,問題文からは読み取れないので消去法にて正答を探すようにしましょう。
(5)解答:ヨ
題意より解答候補は,(イ)平滑化,(ヨ)同期化,等になると思います。
ワンポイント解説「6.誘導発電機の同期発電機と比較した特徴」の通り,誘導発電機は同期発電機と異なり,始動が簡単で,同期化の必要がありません。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん