《機械》〈パワーエレクトロニクス〉[H21:問3]三相インバータで駆動する交流電動機に関する空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，三相インバータで駆動される交流電動機の電位の変動に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切な語句又は式を解答群の中から選び，その記号をマークシートに記入しなさい。

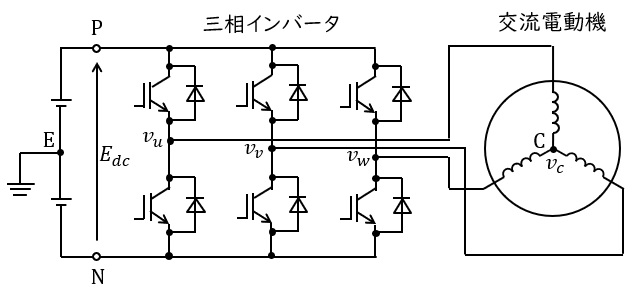
図は，三相インバータで交流電動機を駆動する場合の回路を示す。インバータの直流電源電圧を$ \ E_{dc} \ $として，直流電源の中点$ \ \mathrm {E} \ $を接地した場合，運転しているインバータの出力の各相電位は直流プラス端子$ \ \mathrm {P} \ $の電位$ \ \displaystyle \frac {E_{dc}}{2} \ $か，直流マイナス端子$ \ \mathrm {N} \ $の電位$ \ \displaystyle -\frac {E_{dc}}{2} \ $のいずれかとなる。

各相電位を$ \ v_{u} \ $，$ \ v_{v} \ $，$ \ v_{w} \ $とし，交流電動機の巻線は平衡で星形接続されているものとすると，その星形に接続された点$ \ \mathrm {C} \ $の電位$ \ v_{c} \ $は，$ \ v_{u} \ $，$ \ v_{v} \ $及び$ \ v_{w} \ $を用いて，
\[
\begin{eqnarray}
v_{c} &=& \ \fbox {　（１）　} \ \\[ 5pt ] \end{eqnarray}
\] と表され，各相の出力状態によって変動する。一般的に$ \ \fbox {　（２）　} \ $電位と呼ばれるこの電位は，接地電位に対して変動する電位という見方からコモンモード電位と呼ばれることもある。$ \ \mathrm {PWM} \ $制御の方法によってパワー半導体デバイスの導通パターンは異なるが，組み合わせが可能なすべてのパターンまで含めると，電位$ \ v_{c} \ $がとり得る値は，$ \ E_{dc} \ $を用いると$ \ \fbox {　（３）　} \ $となる。

インバータの運転によるこれらの電位の変動は，パワー半導体デバイスの$ \ \fbox {　（４）　} \ $に起因したものであるから急しゅんな変動である。したがって，出力ケーブル，交流電動機などと対地との間の$ \ \fbox {　（５）　} \ $を通して高周波漏れ電流になって周囲の機器に障害を起こしたり，又は交流電動機のベアリングを電流が流れることによって劣化させたりすることがある。三相インバータ，交流電動機あるいは交流電動機負荷側の機器などの設置状況によってこの現象は異なるので，対地電位の時間的な変化量を抑制するなどの対策が検討される。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　中間点　　　　　&（ロ）&　スイッチング　　　　　&（ハ）&　\frac {1}{3}\left( v_{u}+v_{v}+v_{w}\right) \\[ 5pt ] &（ニ）&　漂遊インダクタンス　　　　　&（ホ）&　電磁誘導　　　　　&（ヘ）&　漏れ電流 \\[ 5pt ] &（ト）&　v_{u}+v_{v}+v_{w}　　　　　　　&（チ）&　中性点　　　　　&（リ）&　導通抵抗 \\[ 5pt ] &（ヌ）&　漂遊静電容量　　　　　&（ル）&　\frac {1}{6}\left( v_{u}+v_{v}+v_{w}\right)　&& \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ヲ）&　ディファレンシャルモード（ノーマルモード） \\[ 5pt ] &（ワ）&　-\frac {E_{dc}}{6},+\frac {E_{dc}}{6} \ の二つ \\[ 5pt ] &（カ）&　-\frac {E_{dc}}{2},-\frac {E_{dc}}{6},+\frac {E_{dc}}{6},+\frac {E_{dc}}{2} \ の四つ \\[ 5pt ] &（ヨ）&　-\frac {E_{dc}}{2},-\frac {E_{dc}}{3},-\frac {E_{dc}}{6},+\frac {E_{dc}}{6},+\frac {E_{dc}}{3},+\frac {E_{dc}}{2} \ の六つ \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

三相インバータの特徴とその出力電圧に関する問題です。
三相インバータのメカニズムを十分に理解しているかを問われています。
二次試験にも出題される可能性がある内容なので，ただ問題が解けるようになるだけでなく，その動作原理は理解しておくようにしましょう。

1.三相インバータの動作
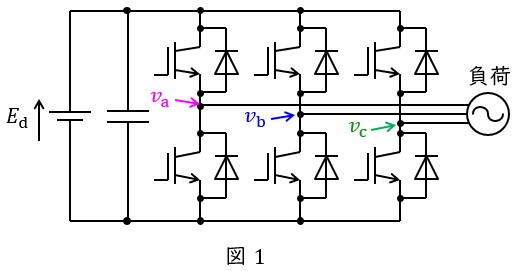
三相インバータは直流から交流を得る回路で，図1のような$ \ 6 \ $つのスイッチで構成されています。
例えば，対応する正負のスイッチを$ \ \displaystyle \frac {2}{3}\pi \ $ずつずらしてオンオフ制御すると，図2のように$ \ \displaystyle \frac {2}{3}\pi \ $ずつずれた方形波が得られ，線間電圧を取れば図3のようなより正弦波に近い波形が得られます。
このとき，線間電圧の実効値$ \ V \ $は，
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }E_{\mathrm {d}}^{2}\mathrm {d}\theta } \\[ 5pt ] &=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }1\mathrm {d}\theta } \\[ 5pt ] &=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left[ \theta \right] _{0}^{\frac {2}{3}\pi }} \\[ 5pt ] &=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left( \frac {2}{3}\pi -0 \right) } \\[ 5pt ] &=&\sqrt {\frac {2}{3}}E_{\mathrm {d}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ハ
題意より解答候補は，（ハ）$ \ \displaystyle \frac {1}{3}\left( v_{u}+v_{v}+v_{w}\right) \ $，（ト）$ \ \displaystyle v_{u}+v_{v}+v_{w} \ $，（ル）$ \ \displaystyle \frac {1}{6}\left( v_{u}+v_{v}+v_{w}\right) \ $，になると思います。
交流電動機の巻線は平衡で星形接続されているものとすると，その星形に接続された点$ \ \mathrm {C} \ $の電位は，$ \ v_{u} \ $，$ \ v_{v} \ $，$ \ v_{w} \ $の平均値となるので，
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( v_{u}+v_{v}+v_{w}\right) \\[ 5pt ] \end{eqnarray}
\] が出力されます。

(2)解答：チ
題意より解答候補は，（イ）中間点，（チ）中性点，（ヲ）ディファレンシャルモード（ノーマルモード），になると思います。
交流電動機の星形に接続された点$ \ \mathrm {C} \ $の電位を一般に中性点電位といいます。

(3)解答：カ
題意より解答候補は，（ワ）$ \ \displaystyle -\frac {E_{dc}}{6},+\frac {E_{dc}}{6} \ $の二つ，（カ）$ \ \displaystyle -\frac {E_{dc}}{2},-\frac {E_{dc}}{6},+\frac {E_{dc}}{6},+\frac {E_{dc}}{2} \ $の四つ，（ヨ）$ \ \displaystyle -\frac {E_{dc}}{2},-\frac {E_{dc}}{3},-\frac {E_{dc}}{6},+\frac {E_{dc}}{6},+\frac {E_{dc}}{3},+\frac {E_{dc}}{2} \ $の六つ，になると思います。
各相電位$ \ v_{u} \ $，$ \ v_{v} \ $，$ \ v_{w} \ $それぞれに$ \ \displaystyle \frac {E_{dc}}{2} \ $もしくは$ \ \displaystyle -\frac {E_{dc}}{2} \ $の電位を取るので，

①$ \ \displaystyle v_{u}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( \frac {E_{dc}}{2}+\frac {E_{dc}}{2}+\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&\frac {E_{dc}}{2} \\[ 5pt ] \end{eqnarray}
\]

②$ \ \displaystyle v_{u}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( -\frac {E_{dc}}{2}+\frac {E_{dc}}{2}+\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&\frac {E_{dc}}{6} \\[ 5pt ] \end{eqnarray}
\]

③$ \ \displaystyle v_{u}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( \frac {E_{dc}}{2}-\frac {E_{dc}}{2}+\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&\frac {E_{dc}}{6} \\[ 5pt ] \end{eqnarray}
\]

④$ \ \displaystyle v_{u}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=-\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( \frac {E_{dc}}{2}+\frac {E_{dc}}{2}-\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&\frac {E_{dc}}{6} \\[ 5pt ] \end{eqnarray}
\]

⑤$ \ \displaystyle v_{u}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( -\frac {E_{dc}}{2}-\frac {E_{dc}}{2}+\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&-\frac {E_{dc}}{6} \\[ 5pt ] \end{eqnarray}
\]

⑥$ \ \displaystyle v_{u}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=-\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( -\frac {E_{dc}}{2}+\frac {E_{dc}}{2}-\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&-\frac {E_{dc}}{6} \\[ 5pt ] \end{eqnarray}
\]

⑦$ \ \displaystyle v_{u}=\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=-\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( \frac {E_{dc}}{2}-\frac {E_{dc}}{2}-\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&-\frac {E_{dc}}{6} \\[ 5pt ] \end{eqnarray}
\]

⑧$ \ \displaystyle v_{u}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{v}=-\frac {E_{dc}}{2} \ $，$ \ \displaystyle v_{w}=-\frac {E_{dc}}{2} \ $のとき
\[
\begin{eqnarray}
v_{c} &=&\frac {1}{3}\left( -\frac {E_{dc}}{2}-\frac {E_{dc}}{2}-\frac {E_{dc}}{2}\right) \\[ 5pt ] &=&-\frac {E_{dc}}{2} \\[ 5pt ] \end{eqnarray}
\]

となり，電位$ \ v_{c} \ $がとり得る値は，$ \ \displaystyle -\frac {E_{dc}}{2},-\frac {E_{dc}}{6},+\frac {E_{dc}}{6},+\frac {E_{dc}}{2} \ $の四つと求められます。

(4)解答：ロ
題意より解答候補は，（ロ）スイッチング，（ホ）電磁誘導，（ヘ）漏れ電流，になると思います。
ワンポイント解説「1.三相インバータの動作」の通り，電位の変動はパワー半導体デバイスのスイッチングに起因したものとなります。

(5)解答：ヌ
題意より解答候補は，（ニ）漂遊インダクタンス，（リ）導通抵抗，（ヌ）漂遊静電容量，になると思います。
前後の出力ケーブルや高周波漏れ電流がヒントとなっていますが，漂遊静電容量によるインピーダンスは高周波になると小さくなるため，高周波漏れ電流になって周囲の機器に障害を起こす可能性があります。